Vector Decomposition and Vector Products
Vector Decomposition and Vector Products
Background and Simulation Information
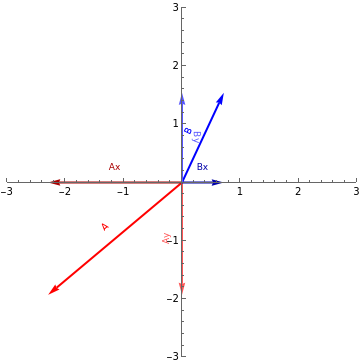
This simulation creates vector decompositions and helps you visualize the dot and cross products of two vectors that lie in the same plane. and its components will be shown in red, while anditscomponentswillbeshowninblueRecall (e.g. from class), that the dot product multiplies parallel components of vectors together and ignores components that are perpendicular entirely. The cross product does the opposite, it multiplies perpendicular components together while ignoring parallel ones. The usage of these two objects might not be obvious yet, so consider an example. If a box is sliding across a table, pushing directly up on the box won’t make it speed up or slow down, but applying a force against its motion will make a difference in the objects speed. Thus the closer a force is to being parallel to the velocity of the box, the larger the contribution. The cross product is a little tougher. Go find a cylindrical object like a water bottle. Now put the cylinder on a flat surface so that it is free to roll. Put your finger on the top and push straight down..The cylinder won’t rotate. If you keep your finger in the same place and apply a force that isn’t straight down, the cylinder will begin to roll. In this case, the closer the force is to being perpendicular to the radius of the cylinder, the larger the spin will be.
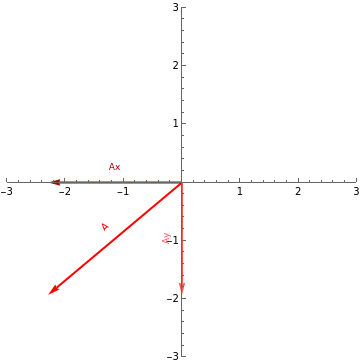
A
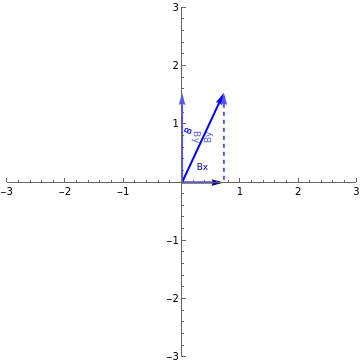
B
Instructions
1
.Think about a vector in the x-y plane. The vector can be thought of as a sum of a vector that points only in the x direction, and one that points only in the y direction. We call these component vectors. We want to make sure that we understand the lengths of those components. Go ahead and play with the simulation for a minute and watch what happens to the A vector decomposition when you change the angle and length of vector A. Pay particular attention to what happens if A is purely along the x or y axis.
2
.If it isn’t obvious yet where the values for the component vectors come from, look at the second panel on the left. In this panel, we are using that the starting point of a vector doesn’t matter. We can translate the vector’s start anywhere we want to; as long as we don’t change the magnitude or the direction that it points, it is the same vector. The dashed version of , and form a right triangle. Recall from your previous trig knowledge the definitions of sine and cosine. Now we can see that the x component is given by Bcosθ and the y component is given by Bsinθ assuming that we are measuring theta from the x axis. This panel should also make it easy to see why a vector can be expressed as a sum of two components that lie in the x and y directions. It doesn’t matter whether you got to the end of vector B by traveling directly along B, or by traveling along the x component followed by the y component. You are at the end of B either way.
B
y
B
x
B
B
x
B
x
3
.Now we focus on the dot product. We want to define the dot product so that it multiplies parallel components together and ignores perpendicular ones. We would also like it to have the usual properties of multiplication (eg associativity, commutativity). Here is a process we might use to come up with a definition that fits this criteria.
3
.1
.First look at the top left pane. What portion of Ax is parallel to Ay? Modify the angle that A makes and its length. You might try to find a case where Ax and Ay are not parallel, but this is impossible. We defined Ax and Ay to be the components that point along x and y respectively. They are always perpendicular. This means that the dot product of two component vectors along different axes must give 0 always.
3
.2
.Now we recall (or learn for the first time) the definition of the unit vectors . Each of these is defined as a vector of length 1 that points along the chosen direction. Since our definition of the dot product asks us to multiply the parallel components together, the dot product must have the property that any unit vector dotted with itself gives 1, and any unit vector dotted with another unit vector gives 0. If you want to visualize the x and y unit vectors, set the length of A to 1.4 and the angle to 45 degrees. You will have the x and y unit vectors.
,,
x
y
z
3
.3
.We learned earlier that any vector can be expressed in terms of its component vectors. Those components are just some number in some direction, in other words, +.
A
A
x
x
A
y
y
3
.4
.It’s not obvious, but we actually already gave all the information we need to define the dot product. Consider the dot product of A and B. ·+·++. If the second equality isn’t obvious, go ahead and multiply it out like regular multiplication. The only thing to remember is our new rule that the dot product of a unit vector with itself is 1 and the dot product of a unit vector with another unit vector is 0
A
B
A
x
x
A
y
y
B
x
x
B
y
y
A
x
B
x
A
y
B
y
4
.Now we want to visualize this and see what we can learn.
4
.1
.Play with the values of A and B and watch the top right pane. What can you do to make the dot product as large as possible? When is the dot product negative? How can you relate that with the definition given earlier?
4
.2
.You hopefully noticed that the dot product is largest when the vectors point in the same direction and that the further apart that the vectors point, the smaller the product gets. This might already be a hint that the dot product has something to do with cosine, but we would like to elucidate this more.
4
.3
.Play with A and B. Notice that, unless the vectors lie in the same quadrant, there is some component of each vector that points in a direction opposite the corresponding component of the other vector (eg maybe Ax points right and Bx points left). This, results from the sign changes that sine and cosine undergo as you change quadrants.
4
.4
.Now set the vectors so that they appear to be about 90 degrees apart. You should notice that the dot product is 0. You can try this a few times until you are convinced that this happens for all possible combinations of A and B that result in perpendicular vectors. Now measure the components of each vector and manually compute the dot product. You should get 0.
4
.5
.Now, multiply out the dot product ·+·++ remembering that Acos and so on. Together with the add angle formula for cosine, you should be able to show that ·ABcos where is the angle between A and B. Thus, the dot product is deeply related to the cosine of an angle.
A
B
A
x
x
A
y
y
B
x
x
B
y
y
A
x
B
x
A
y
B
y
A
x
θ
1
A
B
θ
AB
θ
AB
5
.Finally we look at the cross product. The cross product will be defined so that returns a vector perpendicular to both A and B whose magnitude is the magnitude of the perpendicular components multiplied together. If you want to know why the cross product should return a vector instead of a scalar, there are some good reasons that come from more advanced math, but for now, we just defined it that way. Play with the simulations until you convince yourself that no vector in the x-y plane is perpendicular to both A and B. Fortunately, such a vector does exist. We know that the z direction is perpendicular to both x and y. The only question is whether we should pick positive z or negative z. We adopt a (somewhat arbitrary) convention that each of these equalities should hold.
A
B
5
.1
.
x
y
z
y
z
x
z
x
y
5
.2
.If the same unit vector is multiplied together, we will get 0 because none of a vector is perpendicular to itself.
5
.3
.The cross product is anti-commutative. This means that - for all vectors.
A
B
B
A
5
.4
.If we let + and +, then the cross product will be (using the rules defined above) will be ++. Using the rules above we simplify this to -. Now We want to try to understand this object.
A
A
x
x
A
y
y
B
B
x
x
B
y
y
A
B
A
x
x
A
y
y
B
x
x
B
y
y
A
B
A
x
B
y
z
B
x
A
y
z
5
.5
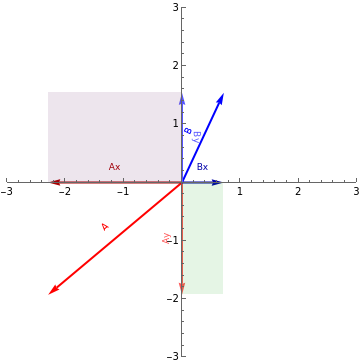
.Look now at the second simulation on the right. As you rotate the vectors, this shows the area of the two rectangles formed by multiplying perpendicular components of A and B together. Notice that when vectors are parallel or anti-parallel, both components are either positive or negative. Calculate the approximate areas of two rectangles here. What happens when we subtract them?
5
.5
.1
.What happens when you make the two vectors perpendicular? Verify that the result is general by changing the vectors a few times.
5
.5
.2
.Notice that at 90 degrees apart, the cross product takes its largest value, and at 0 degrees it is 0.
5
.6
.Now look at the dot and cross products together. Notice that +||isaconstant.Whydoyouthinkthatmightbe?
2
·
A
B
A
B
2
||
6
.
Out[]=
Out[]=