Hertzian Contact Stress

geometry

(mm)

1.8

(mm)

2.4

(mm)

plane

material

(GPa)

207

0.3

(GPa)

207

0.3

mechanics

Q(N)

100

contact zone

colors

a =	0.213	(mm)
b =	0.070	(mm)
A =	0.047	( 2 mm )
r =	3.050
P max =	3200.	(MPa)
P =	2130.	(MPa)
δ =	0.006	(mm)

Over a century ago Hertz established a theory of contact mechanics that is still used today by engineers working in tribology. To make his theory accessible for engineering applications, the program calculates a fast and accurate solution.

This Demonstration presents the Hertzian contact stress distribution and elastic deformations. It uses a color function to visualize the contact zone between a statically loaded pair of contact models, a sphere and a torus. In bearing engineering, the equalized terms are between balls and an inner or outer ring.

Details

Snapshot 1: an approximate point contact zone— two surfaces touch at a single point

Snapshot 2: a typical elliptical contact zone between a ball and an inner ring in a ball bearing assembly

Snapshot 3: a typical elliptical contact zone between a ball and an outer ring in a ball bearing assembly

All calculations are in standard international (SI) or metric system units.

is the geometry parameter of contact body one (radius of ball in red).

is the geometry parameter of contact body two (radius of raceway in green).

is the geometry parameter of contact body two (the distance from raceway bottom to shaft axes).

and

are moduli of elasticity of the contact bodies one and two.

and

are the Poisson's ratios of contact bodies one and two.

is the force between the two contact bodies (ball and raceway).

The top-left plot shows in 3D the geometry of the two contact bodies, especially relevantt for ball bearing engineering analysis.

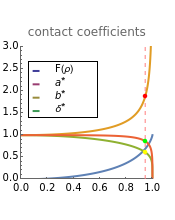
The top-right plot shows the contact coefficient data based on numerical methods to solve elliptic integrals equations.

ρ is the curvature of the contact body surface, that is the reciprocal of the curvature radius of body,

ρ=

∑ρ

is the curvature sum,

∑ρ=

II1

II2

. The subscripts I and II are for the first and second contact bodies. The subscripts 1 and 2 are for the first and second planes of the contact bodies.

F(ρ)