A Visual Proof of the Cauchy-Schwarz Inequality in 2D

​
|a|
|b|
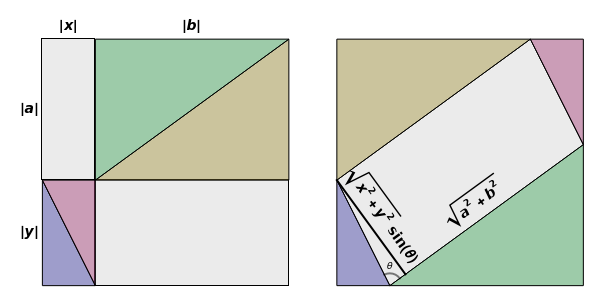
This illustrates the Cauchy-Schwarz inequality in two dimensions, which states:
ax+by=
2
a
+
2
b
2
x
+
2
y
sin(θ)⟹a,b·x,y≤a,bx,y
.
The gray area on the left is
ax+by=|〈a,b〉·〈x,y〉|
. The same gray area in the right hand image is
2
a
+
2
b
2
x
+
2
y
sin(θ)=〈a,b〉〈x,y〉sin(θ)
. For
0≤θ≤
π
2
,
0≤sin(θ)≤1
, hence the inequality.

Details

This image is from S. H. Kung, "Proof without Words: The Cauchy-Schwarz Inequality," Mathematics Magazine, 81(1), 2008 p. 69.

External Links

Cauchy's Inequality (Wolfram MathWorld)

Permanent Citation

Chris Boucher
​
​"A Visual Proof of the Cauchy-Schwarz Inequality in 2D"​
​http://demonstrations.wolfram.com/AVisualProofOfTheCauchySchwarzInequalityIn2D/​
​Wolfram Demonstrations Project​
​Published: March 7, 2011