Calculate true Lagrange interpolating polynomial

={-2,-1,0,1,2};
(Local) In[]:=
={0,-1,0,0,2};
(Local) In[]:=
N_deg=Length[]-1
(Local) Out[]=
4
(Local) In[]:=
X=Block[{ones=Table[1,{i,N_deg+1}]},​​Transpose[Join[{ones},Table[^i,{i,1,N_deg}]]]​​];
(Local) In[]:=
X//MatrixForm
(Local) Out[]//MatrixForm=
1
-2
4
-8
16
1
-1
1
-1
1
1
0
0
0
0
1
1
1
1
1
1
2
4
8
16
(Local) In[]:=
=Inverse[X].
(Local) Out[]=
0,
1
2
,-
3
4
,0,
1
4

(Local) In[]:=
p[x_]=.Join[{1},Table[x^i,{i,1,N_deg}]]
(Local) Out[]=
x
2
-
3
2
x
4
+
4
x
4
(Local) In[]:=
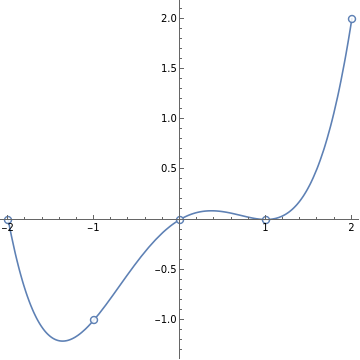
plt1=Plot[p[x],{x,-2,2}];
(Local) In[]:=
plt2=ListPlot[Transpose[{,}],PlotMarkers"OpenMarkers"];
(Local) In[]:=
Show[plt1,plt2,AspectRatio->1]
(Local) Out[]=

Neville’s Algorithm

(Local) In[]:=
NevilleInterpolation[_List,_List,x_]:=Block[{P},​​N_deg=Length[]-1;​​Assert[N_deg>=0];​​Assert[Length[]==N_deg];​​P=Table[0,{i,0,N_deg},{k,0,N_deg}];​​​​P[[;;,1]]=;​​For[k=1,k<=N_deg,++k,​​For[i=k,i<=N_deg,++i,​​P[[1+i,1+k]]=P[[1+i,k]]+(x-[[1+i]])*(P[[1+i,k]]-P[[i,k]])/([[1+i]]-[[1+i-k]])​​]​​];​​P[[N_deg+1,N_deg+1]]​​]
(Local) In[]:=
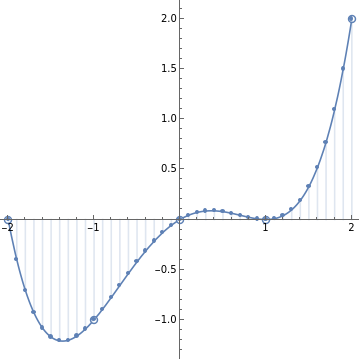
plt3=DiscretePlot[NevilleInterpolation[,,x],{x,-2,2,0.1}];
(Local) In[]:=
Show[plt1,plt2,plt3,AspectRatio->1]
(Local) Out[]=