Constructing directed graphs of email conversationsAbstract: InboxGraph is a property graph representation of mail server archive data, in which message collections are presented in a higher-dimensional space than is possible with traditional user interfaces with linear timestamped constraints. RFC-822 message parsing is used to extract message trajectories between servers and network participants, forming a metadata-rich lattice of vertices and edges inside a directed graph. Asymmetrical relationships between participants are used to calculate Address Rank measurements of information flow importance and to partition the graph into best-fitting communities, opening new channels for organizational optimization. Additional layers of natural language processing and data export to open formats permit further interactive exploration, querying, and discovery of deeper associations within the graph.
Section 1. Community partitioning & Time series helpers
Linear time series subgraph construction and best-fitting community functions.
Linear time series subgraph construction and best-fitting community functions.
In[]:=
(*GetGraphPartitionGroupsreturnsthebest-fittingsubgrouppartitioningforacollectionofoverlappinggroups.*)GetGraphPartitionGroups[subgroups_List]:=Module[{uniqueItems,e,g,p},(*GetOccurLengthreturnsthenumberofsubgroupsco-occurances.*)GetOccurLength[groups_,{i_,j_}]:=Count[ContainsAll[#,{i,j}]&/@groups,True];uniqueItems=Flatten[subgroups]//DeleteDuplicates;(*Constructgraphpartitioningedgesforsubgroupsusingco-occurancecounts.*)e=DeleteCases[If[Unequal@@#,{UndirectedEdge@@#,GetOccurLength[subgroups,#]},Nothing]&/@Subsets[uniqueItems,{2}],{_,0}];(*Constructgraphusingco-occurencesasedgeweights.*)g=Graph[e[[All,1]],EdgeWeighte[[All,2]],VertexLabelsAutomatic,EdgeLabels"EdgeWeight"];(*Addremainingisolatedsubgroups.*)g=VertexAdd[g,Complement[uniqueItems,VertexList[g]]];(*Partitionbyedgeweightsumminimization.*)p=If[Length[#]>1,FindGraphPartition[Subgraph[g,#]],{#}]&/@ConnectedComponents[g];Join@@p](*BuildLinkedGraphcreatesadirectedlinearlistofverticeswithoptionaltooltips*)Options[BuildLinkedGraph]={"ShowTooltip"False};BuildLinkedGraph[v_List,OptionsPattern[]]:=(Graph[v,MapIndexed[v[[#2[[1]]]]#1&,v[[2;;]]],VertexLabels{#If[OptionValue["ShowTooltip"],Placed[#,Tooltip],#]}&/@v]//Flatten)
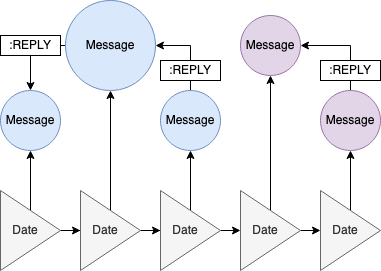
Section 2. Directed InboxGraph visualization.Visualize a MBOX archive thread flow diagram.(Example uses a mailing list archive from https://lists.apache.org.)
In[]:=
(*BuildInboxGraphcreatesadirectedgraphusingmessageidentifiersandoriginatingdateswithgraphpartitioncoloringbysubgraphaddressparticipation.*)Options[BuildInboxGraph]={"FilePath"SystemDialogInput["FileOpen"],"UseTimeSeries"True,"ShowTimeSeries"False,"VertexSizeRange"{0.25,1.0}};BuildInboxGraph[OptionsPattern[]]:=((*Fieldstoimport.*)fields={"MessageID","OriginatingDate","Subject","Body","ReplyToMessageID","FromAddress","ToAddressList","CcAddressList","BccAddressList","ReplyToAddressList"};(*Importmailbox.*)mboxData=<||>;AssociateTo[mboxData,(*KeybyMessageID.*)(#[[1]]AssociationThread[fields,#])&/@Transpose[Import[OptionValue["FilePath"],{"MBOX",fields}]]];(*AddNLPFeatureEngineering:Sentimentclassification.*)mboxData=AssociationMap[#[[1]]Join[#[[2]],<|"Sentiment"Classify["Sentiment",#[[2]]["Body"]]|>]&,mboxData];(*Buildtimeseriesbackbone.*)vDates=DateObject[#,"Day"]&/@Sort[DeleteDuplicates[#[fields[[2]]]&/@Values[mboxData]]]//DeleteDuplicates;eDates=MapIndexed[vDates[[#2[[1]]]]#1&,vDates[[2;;]]];sDates=MapIndexed[vDates[[#2[[1]]]]0.0&,vDates[[2;;]]];vDatesColors=MapIndexed[vDates[[#2[[1]]]]Gray&,vDates[[2;;]]];vDatesShapes=MapIndexed[vDates[[#2[[1]]]]If[OptionValue["ShowTimeSeries"],(*Optionaltimeseriesbackbonevisualization.*)"Circle",None]&,vDates[[2;;]]];(*Buildmessagethreadedges.*)vMsgs=Keys[mboxData];lMsgs=Flatten[{#->Placed[mboxData[#],Tooltip]}&/@vMsgs];eMsgs=Values[Map[#ReplyToMessageID#MessageID&,Select[mboxData,#ReplyToMessageID=!=None&&MemberQ[vMsgs,#ReplyToMessageID]&]]];gMsgs=Graph[vMsgs,eMsgs];(*Connectmessageverticestorelevanttimeseriesanchorvertices.*)eMsgDates=Flatten[{DateObject[mboxData[#][fields[[2]]],"Day"]#}&/@vMsgs];(*CalculatemessageimportancebyVertexDegree*)g=Graph[vMsgs,eMsgs];sMsgs=KeyValueMap[##2&,AssociationThread[VertexList[g],(*ScalevaluesusingVertexSizeRangeparm.*)Rescale[VertexDegree[gMsgs]]*(OptionValue["VertexSizeRange"][[2]]-OptionValue["VertexSizeRange"][[1]])+OptionValue["VertexSizeRange"][[1]]]];(*GetParticipantsreturnsalloftheparticipantsforagivenlistofmessageIDs.*)GetParticipants[msgIDs_]:=(Flatten[Select[Values[KeySelect[mboxData[#],MemberQ[Select[fields,StringContainsQ[#,"Address"]&],#]&]]//Flatten,StringQ(*Validateaddressformatting.*)]&/@msgIDs]//DeleteDuplicates);(*Partitioncommunitybysubgraphco-occuranceedgeweightminimization.*)communitySubgroups=GetGraphPartitionGroups[GetParticipants/@WeaklyConnectedComponents[g]];(*Perceptually-uniformpalettegenerationwithLightness/Chroma/Hueselection.*)communitySubgroupColors=Map[LCHColor[0.5,1,#/Length[communitySubgroups]]&,Range[Length[communitySubgroups]]];(*Createalookuptableforeachaddresscolor.*)communityAddressToColor=<||>;AssociateTo[communityAddressToColor,Flatten[MapIndexed[Function[{community,communityIdx},{#communitySubgroupColors[[communityIdx[[1]]]]}&/@community][#1,#2]&,communitySubgroups]]];(*Colorbythemostcommoncommunityparticipationonamessage.*)vMsgsColors=KeyValueMap[##2&,AssociationThread[vMsgs,Commonest[Flatten[communityAddressToColor/@GetParticipants[{#}]]][[1]]&/@vMsgs]];(*Constructinboxgraph.*)v=vMsgs;l=lMsgs;e=eMsgs;s=sMsgs;c=vMsgsColors;If[OptionValue["UseTimeSeries"],(*Anchormessagestoalineartimeseriesbackbone.*)v=Join[vDates,v];c=Join[vDatesColors,c];e=Join[eDates,eMsgDates,e];s=Join[sDates,s];];(*Colormessagethreadroutingwithoptionaltimeseriesvisualization.*)edgeStyle=If[MatchQ[#[[1]],_DateObject],#If[OptionValue["ShowTimeSeries"],Gray,Transparent],#If[OptionValue["ShowTimeSeries"],Blue,Black]]&/@e;Graph[v,e,VertexLabelsl,VertexSizes,VertexStylec,VertexShapeFunctionvDatesShapes,EdgeStyleedgeStyle,GraphLayout"LayeredDigraphEmbedding"])(*RenderInboxGraphvisualization.*)BuildInboxGraph[UseTimeSeriesTrue,ShowTimeSeriesFalse]
PageRank is a graph analysis algorithm which measures the relative importance of vertices within a directed graph using the number of edge links it receives, the propensity (out-going edges) of the linkers, and the PageRank centrality of the linkers.