Six Incircles in an Equilateral Triangle

d(APC')	≈	0.58	d(BPA')	≈	0.27	d(CPB')	≈	0.35
d(C'PB)	≈	0.51	d(A'PC)	≈	0.25	d(B'PA)	≈	0.44

d(APC')

+

d(BPA')

+

d(CPB')

≈

1.20

d(C'PB)

+

d(A'PC)

+

d(B'PA)

≈

1.20

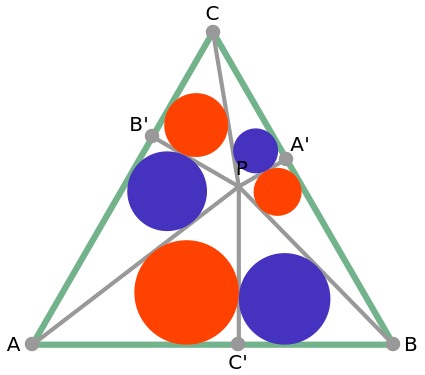
From an interior point P of an equilateral triangle ABC draw lines perpendicular to the sides. Let A', B', and C' be the points on the sides opposite A, B and C. Inscribe circles in the six subtriangles. Let

d

(XYZ) denote the diameter of the incircle in triangle XYZ.

Then the sum of the diameters of the red circles equals the sum of the diameters of the blue circles:

d

(APC') +

d

(BPA') +

d

(CPB') =

d

(C' PB) +

d

(A' PC) +

d

(B' PA)

Details

For more information see Six Incircles in an Equilateral Triangle.

External Links

Equilateral Triangle (Wolfram MathWorld)

Incircle (Wolfram MathWorld)

Permanent Citation

Jay Warendorff

"Six Incircles in an Equilateral Triangle"
http://demonstrations.wolfram.com/SixIncirclesInAnEquilateralTriangle/
Wolfram Demonstrations Project
Published: March 7, 2011