You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
Understanding Convex Hulls
Understanding Convex Hulls
In this notebook, we will explore the concept of the convex hull, a fundamental idea in geometry and computational geometry. We will define the convex hull, discuss its properties, and visualize examples in different dimensions.
Definition of Convex Hull
Definition of Convex Hull
The convex hull of a set of points in a Euclidean space is the smallest convex set that contains all the points. Formally, if S is a set of points {, , ..., }, the convex hull of S, denoted as Conv(S), is defined as:
v
1
v
2
v
k
Conv(S) = {∑( * ) | >= 0, ∑ = 1}
α
k
v
k
α
k
α
k
This means any point in the convex hull can be expressed as a weighted sum (convex combination) of the points in S, where the weights (coefficients) are non-negative and sum to 1.
To understand this better, imagine you have a set of points and you want to find the 'tightest' shape that can enclose all of them. This shape must be convex, which means it does not have any 'dents' or 'inward curves.' If you imagine stretching a rubber band around the set of points, the shape that the rubber band takes is the convex hull.
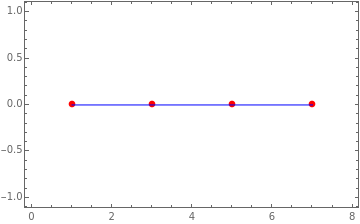
Visualizing Convex Hull in 1D
Visualizing Convex Hull in 1D
In 1D, the convex hull of a set of points is simply the interval (line segment) between the smallest and largest points. For example, if you have points on a number line, the convex hull is the segment that starts at the smallest point and ends at the largest point.
Out[]=
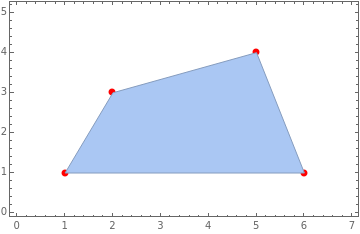
Visualizing Convex Hull in 2D
Visualizing Convex Hull in 2D
In 2D, the convex hull of a set of points can be visualized as the shape formed by stretching a rubber band around the outermost points. Imagine placing some nails on a board and wrapping a rubber band around them. The rubber band will take the shape of the convex hull, which is the smallest polygon that can enclose all the points.
Out[]=
Visualizing Convex Hull in 3D
Visualizing Convex Hull in 3D
In 3D, the convex hull is analogous to wrapping a tight-fitting plastic wrap around the outermost points, forming a convex polyhedron. Imagine you have a set of points in space, and you cover them with a shrink-wrap. The shape that the shrink-wrap takes when it is tight is the convex hull.
Out[]=
Properties of Convex Hull
Properties of Convex Hull
1. Convexity: The convex hull is a convex set, meaning that for any two points in the convex hull, the line segment joining them is also entirely within the convex hull.
2. Minimality: The convex hull is the smallest convex set that contains all the points in S.
3. Inclusion: The original set S is contained within its convex hull, i.e., S ⊆ Conv(S).
2. Minimality: The convex hull is the smallest convex set that contains all the points in S.
3. Inclusion: The original set S is contained within its convex hull, i.e., S ⊆ Conv(S).
Examples
Examples
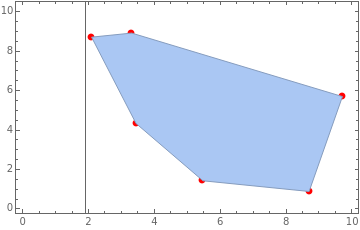
Example 1: Convex Hull of a Set of Points in 2D
Example 1: Convex Hull of a Set of Points in 2D
Out[]=
Example 2: Convex Hull of a Set of Points in 3D
Example 2: Convex Hull of a Set of Points in 3D
Out[]=
