NOTE: evaluate the entire notebook twice for best results.
In[]:=
ClearAll["Global`*"];(*Thisfunctionclearsanypastdefinitionsofthevariables*)

Thermophysical properties of Paraffin

In[]:=
Tm=303;(*meltingtempreratureoftheparaffin*)​​ρs=880;ρl=760;ρ=ρl;(*densityatsolidandliquidstates*)​​ks=0.24;kl=0.15;(*thermalconductivityatsolidandliquidstates*)​​cps=2.4*
3
10
;cpl=1.8*
3
10
;(*specificheatatsolidandliquidstates*)​​q=179*
3
10
;(*latentheatoffusion*)​​vd=3.42;(*dynamicviscosityofparaffin*)​​vk=
vd
ρ
;(*kinematicviscosityofparaffin*)

Parameters

In[]:=
keq=1;(*equivalentthermalconductivity*)​​​​(*sinceRayleighnumber=0(i.e.≤5×
4
10
)forfigure3(c),keqisassumedequalto1*)​​​​​​(*PARAMETERVALUES*)​​​​R=5*
-2
10
;(*radiusofthesphere*)​​Ti=295;(*initialtemperatureoftheparaffin*)​​​​​​(*PARAMETERVALUESSPECIFICTOFIGURE3(c)OFBECHIRIETAL.2020*)​​​​ste=0.05;(*Stefannumber*)​​ra=0;(*Rayleighnumber*)​​bi=10;(*Biotnumber*)​​G=0;(*dimensionlessheatsinkparameter*)​​

Formulas

In[]:=
​​αs=
ks
ρscps
;(*thermaldiffusivityatsolidstate*)​​αl=
kl
ρlcpl
;(*thermaldiffusivityatliquidstate*)​​pr=
vk
αl
;(*Prandtlnumber*)​​gdot=
Gkl(T0-Tm)
2
R
;(*heatsinkparameter*)​​ξ=
gdot
ρq
2
R
τ
αl
;(*massproportionofliquidinthemixture;ttakenas
2
r
τ
αl
*)​​T0=Tm+
qste
cpl
;(*temperatureoutsidethesphere;itdependsonthestefannumberdesiredforthesimulation*)​​​​γ=
ks
kl
;(*solid-to-liquidthermalconductivityratio*)​​Γ=
αs
αl
;(*solid-to-liquidthermaldiffusivityratio*)​​θi=
Ti-Tm
T0-Tm
;(*dimensionlessinitialtemperature*)​​​​λn=
nπ
splus
;
2
λ
n
is the eigenvalue associated with the function
ψ
n
(τ)
for the differential equation ​
dψ
n
(τ)
dη
=-
2
λ
n
Γψ
n
(τ)
.
In[]:=
​

Solution:

In[]:=
θl=-bi
keqτ
Exp
-
2
η
4keqτ

η
-
Exp
-
2
splus
4keqτ

splus
+
π
2
Erfc
splus
2
keqτ
-Erfc
η
2
keqτ
keq
keqτ
Exp
-1
4keqτ
-bi
keqτ
Exp
-1
4keqτ
-
1
splus
Exp
-
2
splus
4keqτ
+
π
2
Erfc
splus
2
keqτ
-Erfc
1
2
keqτ
-
G
6keq
2
splus
-
2
η
+
splus
η
-1
bi(
2
splus
-1)-2keq
bi+splus(keq-bi)
;
In[]:=
θs=-
G
6γ
(
2
splus
-
2
η
)+2Sum
n+1
(-1)
2
λn
θi+
G
2
λn
γ
Sin[λnη]
η
Exp[-
2
λn
Γτ],{n,1,20};
In[]:=
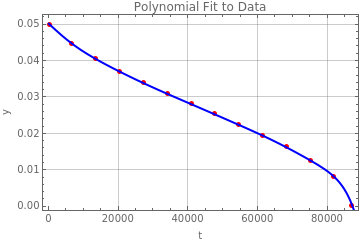
​​​​data3c={{303.712036,0.049948025},{6782.902137,0.04464657},{13667.04162,0.04043659},{20449.94376,0.037006237},{27334.08324,0.033835759},{34116.98538,0.030925156},{41001.12486,0.028066528},{47784.027,0.025259875},{54668.16648,0.022401247},{61552.30596,0.019386694},{68335.2081,0.016216216},{75219.34758,0.012577963},{82002.24972,0.008056133},{87165.35433,0}};​​s=Fit[data3c,{1,t,
2
t
,
3
t
,
4
t
,
5
t
,
6
t
,
7
t
,
8
t
,
9
t
,
10
t
},t];
In[]:=
sFunc[t_]=s;
In[]:=
Show[ListPlot[data3c,PlotStyle->{Red,PointSize[Medium]},PlotLegends->{"Data points"}],Plot[sFunc[t],{t,0,90000},PlotStyle->Blue,PlotLegends->{"Fitted polynomial"}],GridLines->Automatic,Frame->True,FrameLabel->{"t","y"},PlotLabel->"Polynomial Fit to Data"]
Out[]=
Data points
Fitted polynomial

Transformations:

In[]:=
τ=
αlt
2
R
;splus=s/R;η=r/R;
In[]:=
Tl[r_,t_]=θl(T0-Tm)+Tm;​​Ts[r_,t_]=θs(T0-Tm)+Tm;

Visualization:

In[]:=
ManipulatePlot​​​​Piecewise[{{Ts[r,t],0<r<sFunc[t]},{Tl[r,t],r>sFunc[t]}}],​​100sFunc[t]
1-
2
r
sFunc[t]
+Tm,-100sFunc[t]
1-
2
r
sFunc[t]
+Tm​​,​​{r,-R,R},PlotTheme{"Detailed"},AspectRatio1,PlotRange{298,308},PlotLegendsNone,PlotStyle{Red,Blue,Blue},​​FillingStyle{White},Filling{2{3}},Prolog{LightBlue,Scaled/@Rectangle[{0,0},{1,1}]}​​​​,{t,0,24.2*60*60}
Out[]=
​
t
Plot
Ts[r,FE`t$$6680580545055031397886505488047388534467]
0<r<sFunc[FE`t$$6680580545055031397886505488047388534467]
Tl[r,FE`t$$6680580545055031397886505488047388534467]
r>sFunc[FE`t$$6680580545055031397886505488047388534467]
,100sFunc[FE`t$$6680580545055031397886505488047388534467]
1-
2
r
sFunc[FE`t$$6680580545055031397886505488047388534467]
+Tm,-100
sFunc[FE`t$$6680580545055031397886505488047388534467]
1-
2
r
sFunc[FE`t$$6680580545055031397886505488047388534467]
+Tm,{r,-R,R},PlotTheme{Detailed},AspectRatio1,PlotRange{298,308},PlotLegendsNone,PlotStyle{Red,
Blue,Blue},FillingStyle{White},Filling{2{3}},Prolog{LightBlue,Scaled/@Rectangle[{0,0},{1,1}]}