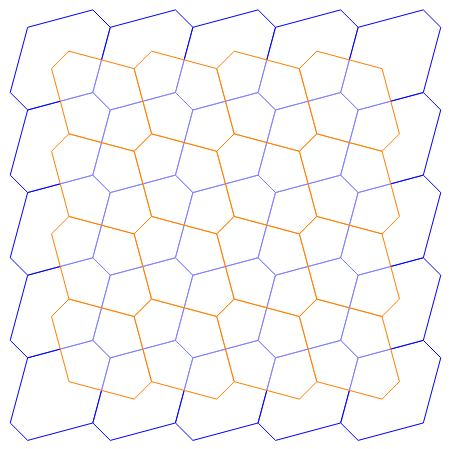
Choe's Hexagon and Cairo Tiling
Choe's Hexagon and Cairo Tiling
What is the minimum perimeter for a tile on the unit square lattice? A unit square has perimeter 4, but this is not minimal. In 1989, Jaigyoung Choe determined the minimal perimeter to be [1]. In this Demonstration, the Choe irregular hexagons are shown in blue (or orange). It turns out that this tile was already well known for hexagons within an optimized Cairo tessellation.
2
+6
≈3.8637References
References
[1] J. Choe, "On the Existence and Regularity of Fundamental Domains with Least Boundary Area," Journal of Differential Geometry, 29(3), 1989 pp. 623–663. 10.4310/jdg/1214443065.
[2] J. Cepelewicz, "Mathematicians Complete Quest to Build 'Spherical Cubes'," Quanta Magazine (Feb 28, 2023). www.quantamagazine.org/mathematicians-complete-quest-to-build-spherical-cubes-20230210/#0.
[3] E. Pegg. "Choe's Irregular Hexagon" from Wolfram Community–A Wolfram Web Resource. community.wolfram.com/groups/-/m/t/2840845.
External Links
External Links
Permanent Citation
Permanent Citation
Ed Pegg Jr
"Choe's Hexagon and Cairo Tiling"
http://demonstrations.wolfram.com/ChoesHexagonAndCairoTiling/
Wolfram Demonstrations Project
Published: March 7, 2023