Mathematica と Geometry Expressions による平面リンク機構の設計と分析
Mathematica と Geometry Expressions による平面リンク機構の設計と分析
◼
執筆者:技術部・上薗
◼
掲載日:2024/01
◼
使用した Mathematica のバージョン:13.3.1.0
◼
使用した Geometry Expressions のバージョン:3.4.20
◼
この記事を Notebook で開く
はじめに
はじめに
Mathematica を使った 「平面リンク機構」 の分析事例は、スライダクランク機構をはじめとしてウルフラムのサイトでも幾つか紹介されています。機構 (メカニズム) をモデル化し、その力学的性質を研究するという分野です。しかし、この最初の段階、すなわち、機構を Mathematica でモデル化するという作業は、それをあらわすコードを一から作成することになりますので、結構手間がかかります。ここでは、平面リンク機構の 「モデル化」 から 「数式化」 を担う部分に幾何学モデルソフトウェア Geometry Expressions を使用することで、作業を大幅に簡素化、効率化できることを紹介します。
I. Geometry Expressions によるモデル設計の基本要素
I. Geometry Expressions によるモデル設計の基本要素
Geometry Expressions で幾何学的図形を定義するには2つの方法があります。もっとも直接的な方法は、描画要素を選んで図形を定義する方法です。円を描くにはマウスで円の中心をクリックして、半径をドラッグして指定します。直線を描くには始点と終点をマウスでクリックするだけです。直角三角形を描くには3つのラインを描画して、条件として各辺に長さを設定したり、2辺の間に角度を設定するだけです。
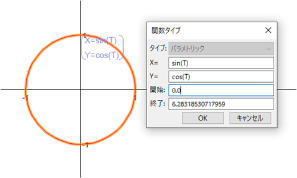
幾何学的図形を定義するもう一つの方法は、関数を定義することです。直交座標に Y = X2、Y = sin (X) といった式を定義して放物線や正弦波を描画したり、パラメトリック座標を使って、パラメータに T を使って、sin (T) と cos (T) で円を描画することができます。※直交座標で利用できる独立変数は X、パラメトリック関数で利用できる媒介変数は T に限定されます。パラメータには任意の文字を利用できます。
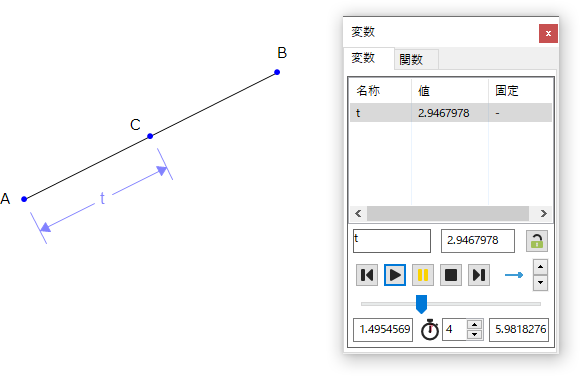
もうひとつ重要な要素は、運動に関する定義です。まず、スライド運動に関する定義です。例えば、直線上にある1点を移動させたい場合。まず、直線 AB を描画します。直線上に点 C を配置します。配置した点に変数 t を定義します。定義した変数を変化させることで直線上の点を動かすことができます。
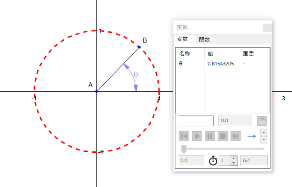
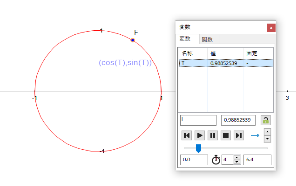
次に、回転運動に関する定義です。回転運動をあらわすには2つの方法があります。ひとつは図形として直接円と半径を描画して、角度θを変化させる方法です。もうひとつは、パラメトリック関数で円を定義して、そのパラメータ T を変化させる方法です。
Geometry Expressions で行う作業は、いたってシンプルです。単純な要素をつなぎ合わせることでより複雑な機構を構築してゆくことができます。次のセクションでは、実際にスライダクランク機構をモデル化する手順を紹介し、その後、得られた数式を Mathematica でどう処理してゆくかを紹介してゆきます。
II. Geometry Expressions でスライダクランク機構を設計する
II. Geometry Expressions でスライダクランク機構を設計する
スライダクランク機構とは、機構学的には3つの 「回り対偶」 と1つの 「すべり対偶」 で結び付けた機構であると定義されます。回転運動とスライド運動が連動するメカニズムです。
Geometry Expressions で作図する内容は、以下のようなものです。
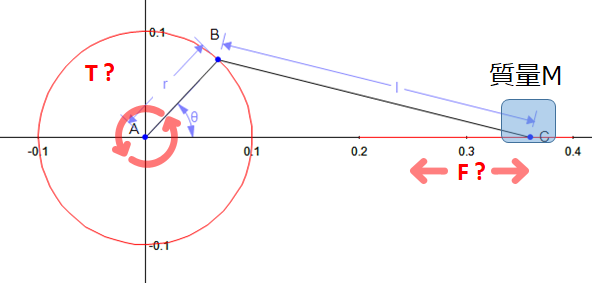
モーターを原動力として往復運動をおこなう装置を、下記要件にて設計する。
◼
円の半径[m]:r = 0.1
◼
アームの長さ[m]:l = 0.3
◼
回転数[rpm]:6000
◼
C の質量[kg] : M = 0.5
上記要件からスライド部分にかかる力 F の大きさを求めます。さらに、力 F にもとづいて最大トルク T[N・m] を求めます。(※問題を単純化するために慣性力や摩擦力といった要素は除外します)
この機構を Geometry Expressions でモデル化し、スライド部分の軌跡の式を求めるまでの手順は以下のようになります。
◼
原点からのびる直線 AB を作成し、長さを r、x 軸との角度を θ として条件を設定する。
◼
θ をパラメータとする軌跡を描画する (赤い円)
◼
点B から x 軸に接続する直線 BC を作成し、長さを l として条件を設定する。
◼
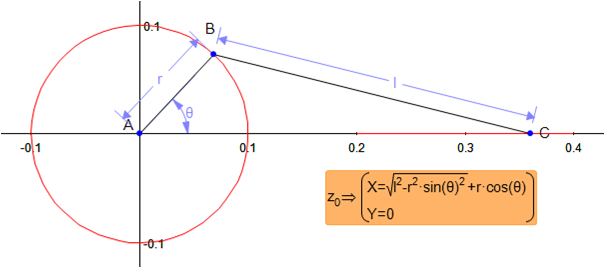
θ をパラメータとするスライド部分の軌跡を描画して (赤い直線)、θ, r, l, を使って軌跡をあらわす数式を求める。オレンジの部分。
III. Mathematica での数式処理
III. Mathematica での数式処理
Geometry Expressions で設計した機構の点 C のスライド運動をあらわす数式を出力したら、その内容をコピーして、 Mathematica にペーストします。
関数 f を定義する
関数 f を定義する
Mathematica にペーストしたパラメトリック関数の X 部分の式を利用して、変位をあらわす関数 f を定義します。※ここで、θ を、角速度ω と時間 t の積に置き換えます。
関数 f をプロットする (x 軸の変位)
関数 f をプロットする (x 軸の変位)
定義した関数 f をそのままの形で時間 t についてプロットします。つまり x 方向の変位をあらわすプロットです。パラメータには r と l と ω がありますが、ω は回転数:6000 rpm より ω = 200 π を代入します。
円の半径 r とアームの長さ l が変われば、結果がどう変わるかをインタラクティブに分かるようにするため、Manipulate 関数を使います。Manipulate では半径 r とバーの長さ l の2つのパラメータを変化させます。r と l の初期値には、要件にあわせて 0.1 と 0.3 を定義します。また r と l の範囲には、それぞれ、0.1 ~0 .2、0.3 ~0 .5 を定義しています。時間の範囲は1回転分の、ゼロから 0.01 の範囲を定義します。
円の半径 r とアームの長さ l が変われば、結果がどう変わるかをインタラクティブに分かるようにするため、Manipulate 関数を使います。Manipulate では半径 r とバーの長さ l の2つのパラメータを変化させます。r と l の初期値には、要件にあわせて 0.1 と 0.3 を定義します。また r と l の範囲には、それぞれ、0.1 ~0 .2、0.3 ~0 .5 を定義しています。時間の範囲は1回転分の、ゼロから 0.01 の範囲を定義します。
関数 f を時間 t で一階微分して速度の変化をプロットする
関数 f を時間 t で一階微分して速度の変化をプロットする
つぎに、速度の変化を Mathematica であらわします。速度は、関数 f を時間 t で1階微分して得られるものとなりますので、Mathematica の関数 D を使って以下ようにあらわすことができます。それ以外は同じパラメータを使います。
関数 f を時間 t で2階微分して加速度 (a[m/s^2]) の変化を求める
関数 f を時間 t で2階微分して加速度 (a[m/s^2]) の変化を求める
次に、加速度の変化をあらわします。加速度は、関数 f を時間 t で2階微分して得られるものとなりますので、Mathematica では以下のようにあらわすことができます。他のパラメータは同じです。
F (力) の変化を求める
F (力) の変化を求める
次に、力の変化を Mathematica であらわします。力は、加速度 ax質量 M で求めることができますので、新たに質量 M を導入して、加速度の式に掛け合わせます。Manipulate のパラメータにも M を追加して、その初期値には 0.5 Kg を指定します。
以上が、Mathematica での式の定義になります。これによって、速度、加速度、力のプロットを求めることができました。
IV. トルクの定義式を求めるまでの手順
IV. トルクの定義式を求めるまでの手順
トルクを求めるには、スライダ部の力 F を使ってこのように求めることができます。つまり、アーム方向の力 F’ と、原点からアームに降ろした垂線の距離 d の積 T = F’ * d です。※ここで単純化のため、慣性力や摩擦力は無視するものとします。
アーム方向の力 F' の大きさと、距離 d の関係式については、Geometry Expressions で幾何学的に求めることができます。少し長い数式なりますが、得られた F’ と d の数式をそれぞれ Mathematica にペーストします。
F' の式をペースト
F' の式をペースト
d の式をペースト
d の式をペースト
トルク T = F'*d のプロット
トルク T = F'*d のプロット
得られた数式を使って、トルクをあらわす数式を作成します。
T (N・m) = F'*d のプロットを絶対値であらわし、最大値を求める
T (N・m) = F'*d のプロットを絶対値であらわし、最大値を求める
F'、d、T のプロットを縦に並べる
F'、d、T のプロットを縦に並べる
V. その他のモデリング例
V. その他のモデリング例
Geometry Expressions を使えば、このモデルに一部修正を加えたり、要素を追加することで、オフセット型のスライダクランク機構やワイパー機構といったより複雑なモデルを作成することもできます。
オフセット型のスライダークランク機構:
オフセット型のスライダークランク機構:
オフセット型のスライダクランク機構は、X 軸から点 C を切り離して、点C と X 軸との間に距離の条件として、新たに h を設定するものです。Geometry Expressions の作図によって得られる数式は以下のとおりです。これによって、C の往復運動の軌跡をあらわす数式に変数 h がどのように関与するかが即座にわかります。
この数式を先ほどと同じ工程で Mathematica で処理すると、h を導入したことで、スライダクランク機構の挙動がどのように変化するかを確認できます。
変数 θ を ω t に置き換えます。ω は角速度、t は時間 (秒) です。
関数 g を定義します。
関数 g をプロットします。(h は x 軸の上下の変位になります)
関数 g を時間 t で微分して速度の変化をプロットします。
関数 g を時間 t で2階微分して加速度 (a[m/s^2]) の変化を求めます。
力 (F[N]) = 加速度 (a[m/s^2]) x 質量 (M[kg]) より、Fの変化を求めます。
変位・速度・加速度を並べて比較します。
ワイパー機構
ワイパー機構
スライダクランク機構にさらに要素を追加すれば、複雑なワイパー機構を作成することも可能です。
VI. HTML5/JavaScript App への出力
VI. HTML5/JavaScript App への出力
Geometry Expressions で作図したモデルは、EPS、EMF、SVG といったベクトル形式の画像のほか、このプレゼンで使用しているアニメーション GIF や、JavaScript を使ったインタラクティブな HTML 形式に出力することができます。これによって Geometry Expressions を持っていない同僚とも容易に情報交換することができます。
以上、Geometry Expressions と Mathematica を使った平面リンク機構についてご説明させていただきました。Geometry Expressions を使うことで如何に容易に平面機構をモデル化し、Mathematica で利用できる数式を出力できるかについて、イメージを掴んでいただけたとおもいます。