WOLFRAM NOTEBOOK

Chemical Informatics

Out[]=
Molecular shape analysis (MSA) is a vital first step in quantitative structure-activity relationships (QSAR) investigations.
Let's classify molecular shapes using the principal moments of inertia (PMI) and visualize the results using a PMI plot.
Consider three molecules with different shapes:
In[]:=
{rod,disk,sphere}={Molecule["Buta-1,3-diyne"],Molecule["benzene"],Molecule["adamantane"]};​​Row[Map[MoleculePlot3D[#,ImageSize->Small]&,{rod,disk,sphere}],Spacer[10]]
Out[]=
Compute 3D coordinates for the molecules and find the principal moments of inertia:
MoleculeValue[{rod,disk,sphere},"PrincipalMoments"]
Out[]=
5.46402×
-12
10
u
2
Å
,
126.042
u
2
Å
,
126.042
u
2
Å
,
88.7257
u
2
Å
,
88.7259
u
2
Å
,
177.452
u
2
Å
,
300.033
u
2
Å
,
300.033
u
2
Å
,
300.034
u
2
Å
Normalize the principal moments by dividing the two smaller moments by the largest moment:
MoleculeValue[{rod,disk,sphere},"NormalizedPrincipalMomentRatios"]
Out[]=
{{4.33507×
-14
10
,1.},{0.499999,0.500001},{0.999999,1.}}
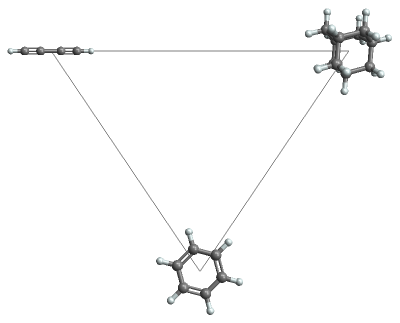
Now use these normalized principal moment ratios (NPRs) as the coordinates in a 2D scatter plot:
insets=Map[Inset[MoleculePlot3D[#],#["NormalizedPrincipalMomentRatios"],Center,.3]&,{rod,disk,sphere}];​​triangle={FaceForm@None,EdgeForm[Gray],Triangle[{{0,1},{1/2,1/2},{1,1}}]};​​background=Graphics[{triangle,insets},ImagePadding45,AspectRatio3/4,ImageSize400]
Out[]=
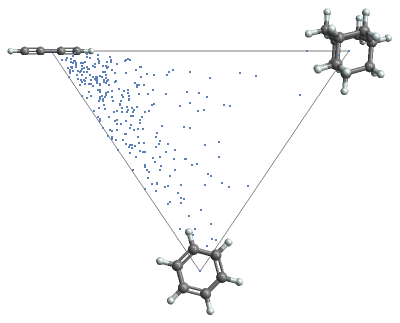
Compare the shape for a collection of molecules, using the principal moment ratios for coordinates and 3D plots for tooltips:
In[]:=
mols=
mols
;​​ResourceFunction["MoleculePrincipalMomentPlot"][mols]
Out[]=
Out[]=
Close
TOC
Wolfram Cloud

You are using a browser not supported by the Wolfram Cloud

Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.


I understand and wish to continue anyway »

You are using a browser not supported by the Wolfram Cloud. Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.