Galileo's Paradox

​
The red and blue beadsfall without friction alongthe green wires.​Can you predict which beadwill reach the bottom first?​Click the "Play" arrow (▶)above to find out!
Use this slider to changethe starting point of thered bead.​Can you explain what youobserve physically ormathematically?​​Hints:
1
2
3
4
5
6
7
8
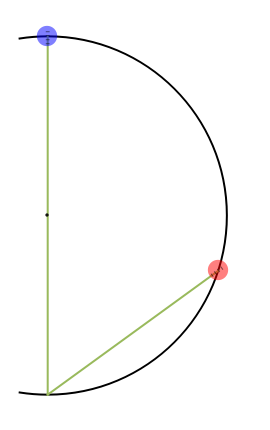
The blue bead falls straight down to the bottom of the circle along the vertical green wire.
The red bead starts at a lower point and slides without fraction diagonally, finishing at the same point as the blue bead.
Can you predict which bead will reach the bottom first?
Activate the trigger to find out!
Can you explain the result? (Click the hints for help.)

Details

Falling objects seem familiar but their behavior can often be contrary to intuition. Here is a chance to see if you can predict the results of a "race" between two bodies falling along different paths towards the same point. Click the "Play" (right arrow ▶) button to start the race and find out! You can use the slider at the left to change the red ball's starting point. Does that change the outcome? Can you explain the results qualitatively? Can you calculate the times of descent for both balls and resolve Galileo's paradox? The snapshots show various starting positions for the red ball. This problem was first mentioned in 1602 by Galileo; see D. B. Meli, Thinking with Objects, Baltimore: Johns Hopkins University Press, 2006 p. 71.
Resolution of the paradox:
Both objects start from rest and are accelerated uniformly by gravity. Therefore the distances traveled (D and L), their accelerations
(
a
blue
and
a
red
), and the times elapsed
(
t
blue
and
t
red
) are related as follows:
D=
1
2
a
blue
2
t
blue
,
L=
1
2
a
red
2
t
red
.
The blue bead accelerates at
g=9.8m/
2
s
. Therefore,
D=
1
2
9.8
2
t
blue
.
Solving for
t
yields:
t
blue
=
2D
9.8
.
However, the red bead moves diagonally and its acceleration is, therefore, proportionally smaller. From the diagram, you can see that acceleration of the red bead will be the diagonal component of acceleration of the blue bead, that is,
a
red
=9.8sin(θ)
. Substituting into
D=
1
2
a
red
2
t
red
yields
L=
1
2
9.8sin(θ)
2
t
red
.
Finally, you can see from the diagram that
sin(θ)=
L
D
. Substituting this into the equation immediately above yields:
L=
1
2
9.8
L
D
2
t
red
.
Solving for
t
red
yields:
t
red
=
2D
9.8
.
This agrees with the time for the blue bead and resolves the paradox.
A faster solution is to divide the two equations
L=
1
2
a
red
2
t
red
and
D=
1
2
a
blue
2
t
blue
, which yields:
L
D
=
a
red
2
t
red
a
blue
2
t
blue
. Since
L
D
=
a
red
a
blue
=sin(θ)
, the two times must be equal. Physically, the blue bead's acceleration is larger than the red bead's acceleration by the same ratio that the distance the blue bead travels is greater than the distance the red bead travels.
Source: T. B. Greenslade, Jr., "Galileo's Paradox," The Physics Teacher, 46(5), 2008 p. 294.

External Links

Galileo Galilei (1564–1642) (ScienceWorld)
Gravity (ScienceWorld)

Permanent Citation

Fernand Brunschwig
​
​"Galileo's Paradox"​
​http://demonstrations.wolfram.com/GalileosParadox/​
​Wolfram Demonstrations Project​
​Published: March 7, 2011