Following the notation of the paper, we have
​
In[]:=
f=6(x^2+κ*y^2)((z-1)*(x^2+y^2+(z-1)^2)^(-5/2)-(z+1)*(x^2+y^2+(z+1)^2)^(-5/2))-(1+κ)((z-1)*(x^2+y^2+(z-1)^2)^(-3/2)-(z+1)*(x^2+y^2+(z+1)^2)^(-3/2))
Out[]=
-
-1+z
3/2
(
2
x
+
2
y
+
2
(-1+z)
)
-
1+z
3/2
(
2
x
+
2
y
+
2
(1+z)
)
(1+κ)+6
-1+z
5/2
(
2
x
+
2
y
+
2
(-1+z)
)
-
1+z
5/2
(
2
x
+
2
y
+
2
(1+z)
)
(
2
x
+
2
y
κ)
In[]:=
integrand=f*(x^2+y^2+(z-1)^2)^(-1/2)
Out[]=
-
-1+z
3/2
(
2
x
+
2
y
+
2
(-1+z)
)
-
1+z
3/2
(
2
x
+
2
y
+
2
(1+z)
)
(1+κ)+6
-1+z
5/2
(
2
x
+
2
y
+
2
(-1+z)
)
-
1+z
5/2
(
2
x
+
2
y
+
2
(1+z)
)
(
2
x
+
2
y
κ)
2
x
+
2
y
+
2
(-1+z)

Converting into cylindrical coordinates
integrandCylindrical=Simplify[ρ*integrand/.{xρ*Cos[ϕ],yρ*Sin[ϕ]}]
Out[]=
ρ-(1+κ)
-1+z
3/2
(1-2z+
2
z
+
2
ρ
)
-
1+z
3/2
(1+2z+
2
z
+
2
ρ
)
+6
2
ρ
-1+z
5/2
(1-2z+
2
z
+
2
ρ
)
-
1+z
5/2
(1+2z+
2
z
+
2
ρ
)
(
2
Cos[ϕ]
+κ
2
Sin[ϕ]
)
1-2z+
2
z
+
2
ρ

Integrating over the angle
In[]:=
integrandRhoZ=Integrate[integrandCylindrical,{ϕ,0,2Pi}]
Out[]=
ρ6π(1+κ)
2
ρ
-1+z
5/2
(
2
(-1+z)
+
2
ρ
)
-
1+z
5/2
(
2
(1+z)
+
2
ρ
)
-2π(1+κ)
-1+z
3/2
(
2
(-1+z)
+
2
ρ
)
-
1+z
3/2
(
2
(1+z)
+
2
ρ
)

1-2z+
2
z
+
2
ρ

Now integrate over the whole planar radii to get the integrand over z
In[]:=
integrandZ=Simplify[Integrate[integrandRhoZ,{ρ,0,Infinity},AssumptionsElement[z,Reals]]]
Out[]=
(π(1+κ)(-
3
(1+z)
(1+
2
z
)
3
Abs[-1+z]
+(1-3z+
3
z
(4+(-3+z)z))
3
Abs[1+z]
))(4
2
(-1+z)
2
z
3
Abs[1+z]
)
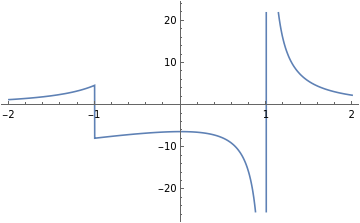
This function has a singularity at z=1. Let's plot it too see how it behaves
In[]:=
Plot[integrandZ/.κ1,{z,-2,2}]
Out[]=
Let's first get the negative part of the integral
In[]:=
integralNegativeDomain=Simplify[Integrate[integrandZ,{z,0,-Infinity}]]
Out[]=
1
4
π(1+κ)
Now let's remove the singularity by introducing a small number ε>0
In[]:=
integralPositiveDomainForEpsilon=FullSimplify[Integrate[integrandZ,{z,0,1-ϵ},Assumptions{0<ϵ<1/2}]+Integrate[integrandZ,{z,1+ϵ,Infinity},Assumptions{0<ϵ<1/2}],Assumptions{0<ϵ<1/2}]
Out[]=
1
4
π(1+κ)-1+
2
ϵ
+2
1
1+ϵ
+Log1+
1
ϵ
+2Log[ϵ]
Now let's approximate this for small ε by expanding to a series and neglecting the higher order terms
In[]:=
integralPositiveDomain=Simplify[Normal[Series[integralPositiveDomainForEpsilon,{ϵ,0,1}]],Assumptions{0<ϵ<1/2}]
Out[]=
1
4
π(1+κ)
The total integral is
In[]:=
integralTotal=integralPositiveDomain+integralNegativeDomain
Out[]=
1
2
π(1+κ)