WOLFRAM NOTEBOOK

The terms and the upper limit point of their partial sums of the MRB constant (CMRB) series:

In[]:=
CMRB=1/2+NSum[
k
(-1)
1/k
k
,{k,1,Infinity},WorkingPrecision30,Method"AlternatingSigns"]
Out[]=
0.1878596424620671202361147732
​
In[]:=
Assuming[q<1,Sum[q^k,{k,1,Infinity}]]
Out[]=
-
q
-1+q
Considerthegeometricsum,​​p=-
q
-1+q
,​​where
k
q
log
x
log(x)
2
x
+π
-
πx
log(q)
.
In[]:=
p=FullSimplify-
q
-1+q
/.Solve[q^k==Log[-E^(I*Pi*x)+E^(x*(I*Pi+Log[x]/x^2))]/Log[q],q]
Solve
:Inverse functions are being used by Solve​, so some solutions may not be found; use Reduce for complete solution information.
p=-1+
1
1-
1
k
ProductLogkLog
πx
-1+
1
x
x

Below, by fixing the value of k, the plot of the terms of the geometric sum of the CMRB looks similar that of the partial sums of the CMRB series.

In[]:=
Show[ListPlot[l=Accumulate[Table[
k
(-1)
1/k
k
,{k,100}]],JoinedTrue,PlotStyleRed,AxesLabel{n,
s
n
}],Plot[CMRB-1,{n,1,100},PlotStyleBlue],Plot[CMRB,{n,1,100},PlotStyleBlue]]
In[]:=
Table[y[n]=ReImPlot[p/.k->n,{x,1,100},PlotStyleGreen],{n,1/100,1,1/100}];
In[]:=
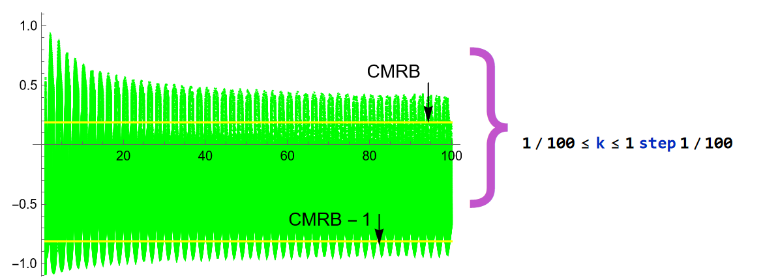
Show[{Table[y[n],{n,1/100,1,1/100}],Plot[CMRB,{n,1,100},PlotStyleYellow],Plot[CMRB-1,{n,1,100},PlotStyleYellow]},PlotRange->{-1,1}]

By fixing the value of k, the real and imaginary parts of this function,
p(x)=-1+
1
1-
1
k
ProductLogkLog
πx
-1+
1
x
x
, go close to the upper and lower limit points of the CMRB series.

In[]:=
Table[y[n]=ReImPlot[p/.k->n,{x,1,100},PlotStyleGreen],{n,1/100,1,1/100}];
In[]:=
p=FullSimplify-
q
-1+q
/.Solve[q^k==Log[-E^(I*Pi*x)+E^(x*(I*Pi+Log[x]/x^2))]/Log[q],q]
In[]:=
p/.k->1
Out[]=
-1+
1
1-
ProductLogLog
πx
-1+
1
x
x
In[]:=
Show[{y[100/100],Plot[CMRB-1,{n,1,100},PlotStyleYellow]},PlotRange->{-1,1}]
p(x)=-1+
1
1-
ProductLogLog
πx
-1+
1
x
x
In[]:=
ShowReImPlot-1+
1
1-
ProductLogLog
πx
-1+
1
x
x
,{x,1,100},PlotStyleBlack,Plot[CMRB,{x,1,100},PlotStyleYellow],Plot[CMRB-1,{x,1,100},PlotStyleYellow]
​
In[]:=
ShowReImPlot-1+
1
1-
ProductLogLog
πx
-1+
1
x
x
,{x,1,1000},Plot[CMRB,{x,1,1000},PlotStyleRed],Plot[CMRB-1,{x,1,1000},PlotStyleBlack]
In[]:=
ShowReImPlot-1+
1
1-
ProductLogLog
πx
-1+
1
x
x
,{x,1,10000},Plot[CMRB,{x,1,10000},PlotStyleRed],Plot[CMRB-1,{x,1,10000},PlotStyleBlack]

However, the details of the geometric sum are rather intricate.

Wolfram Cloud

You are using a browser not supported by the Wolfram Cloud

Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.


I understand and wish to continue anyway »

You are using a browser not supported by the Wolfram Cloud. Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.