1. Using FluidFlowPDEComponent for the Navier-Stokes part

Fluid Dynamics Model

Use of FluidFlowPDEComponent for the Navier-Stokes part was achieved by first comparing the coefficients in the Brinkman momentum equation with the coefficients in the Navier-Stokes momentum equation:
Navier-StokesEquation:0V+
ρV·∇V+∇·(-μ∇V)+∇p
=
0
BrinkmanEquation:
μ
κ
V+0V·∇V+∇·-
μ
ϕ
∇V+∇p
=
F
Thus, FluidFlowPDEComponent can be used to solve the Navier-Stokes part by modifying it in the following way:
1
.
Making the following replacements in the function parameters for region 2:
1
.
1
.
Replacing the mass density ρ with 0.
1
.
2
.
Replacing the dynamic viscosity μ with
μ
ϕ
.
2
.
Adding the term
μ
κ
V
to the function for region 2.
3
.
Defining the continuity equation explicitly in its reduced form
∇·V=0
. This adjustment is necessary because we replaced ρ with 0, which would otherwise cause the continuity equation to become an identity in region 2.
Making the aforementioned modifications in the FluidFlowPDEComponent gives the following flow model:
In[]:=
coupledFlowModel=FluidFlowPDEComponent{{u[x,y],v[x,y],p[x,y]},{x,y}},<|"DynamicViscosity"->IfElementMarker==1,μ,
μ
ϕ
,"MassDensity"->If[ElementMarker==1,ρ,0]|>+IfElementMarker==1,0,
μ
κ
*{u[x,y],v[x,y],0};coupledFlowModel[[-1]]=
(0,1)
v
[x,y]+
(1,0)
u
[x,y];
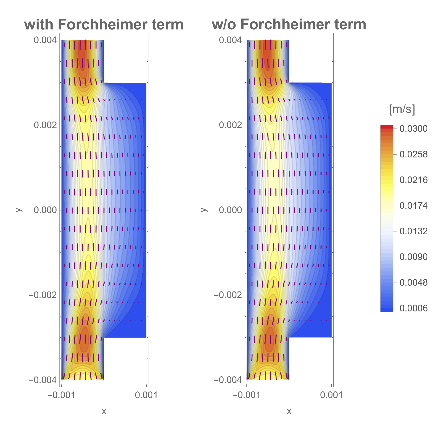
This model reproduces the result of the original notebook provided as shown below.

Model Implementation

In[]:=
Needs["NDSolve`FEM`"];
In[]:=
coordinates=
;
In[]:=
connectivity=
;
In[]:=
bmesh=ToBoundaryMesh["Coordinates"coordinates,"BoundaryElements"connectivity];
In[]:=
freeCoordinate={-5*
-4
10
,0};
In[]:=
porousCoordinate={5*
-4
10
,0};
In[]:=
mesh=ToElementMesh[bmesh,"RegionMarker"->{{freeCoordinate,1},{porousCoordinate,2}},"MaxCellMeasure"{"Length"2*
-4
10
}];
In[]:=
mesh["Wireframe"["MeshElementStyle"{Directive[FaceForm[Green]],Directive[FaceForm[Red]]}]]
Out[]=
In[]:=
μ=
-3
10
(*dynamicviscosity*);​​ρ=1000(*pristinewaterdensity*);​​κ=
-7
10
(*permeability*);​​ϕ=0.4(*porosity*);​​
v
in
=0.02(*inletvelocity*);​​
p
ref
=0(*referencepressure*);​​Cf=
1.75
150
3
ϕ
(*frictioncoefficient*);
In[]:=
{
F
x
,
F
y
}=IfElementMarker1,0,-
ρϕCf
κ
*
2
u[x,y]
+
2
v[x,y]
*{u[x,y],v[x,y]};
In[]:=
Γ
inlet
=DirichletCondition[{u[x,y]0,v[x,y]
v
in
},y-4*
-3
10
];
In[]:=
Γ
outlet
=DirichletCondition[p[x,y]
p
ref
,y4*
-3
10
];
In[]:=
Γ
wall
=DirichletCondition[{u[x,y]0,v[x,y]0},x-
-3
10
||x>0||x0&&(y<-3*
-3
10
||y>3*
-3
10
)];
In[]:=
bcs={
Γ
inlet
,
Γ
outlet
,
Γ
wall
};
In[]:=
pde={coupledFlowModel{0,0,0},bcs};
In[]:=
{ufun,vfun,pfun}=NDSolveValue[pde,{u,v,p},{x,y}∈mesh,"InitialSeeding"{u[x,y]0,v[x,y]
v
in
,p[x,y]0},Method{"PDEDiscretization"{"FiniteElement","InterpolationOrder"{u2,v2,p1}}}];
In[]:=
pde={coupledFlowModel{
F
x
,
F
y
,0},bcs};
In[]:=
{ufunCorrected,vfunCorrected,pfunCorrected}=NDSolveValue[pde,{u,v,p},{x,y}∈mesh,"InitialSeeding"{u[x,y]ufun[x,y],v[x,y]vfun[x,y],p[x,y]0},Method{"PDEDiscretization"{"FiniteElement","InterpolationOrder"{u2,v2,p1}}}];
In[]:=
g1=
Show[
]
;​​g2=
Show[
]
;​​lis=
Rasterize[
]
&/@{g1,g2};​​GraphicsRow[lis]
Out[]=
In[]:=
Plot
2
ufun[x,0]
+
2
vfun[x,0]
,
2
ufunCorrected[x,0]
+
2
vfunCorrected[x,0]
,x,-
1
3
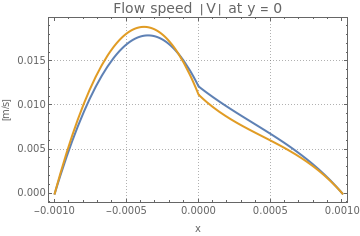
10
,
1
3
10
,PlotTheme"Detailed",PlotLegends{"with correction","w/o correction"},PlotLabelStyle["Flow speed V at y = 0",14],FrameLabel{"x","[m/s]"},ImageSizeMedium
Out[]=
with correction
w/o correction