DIGITOXINE
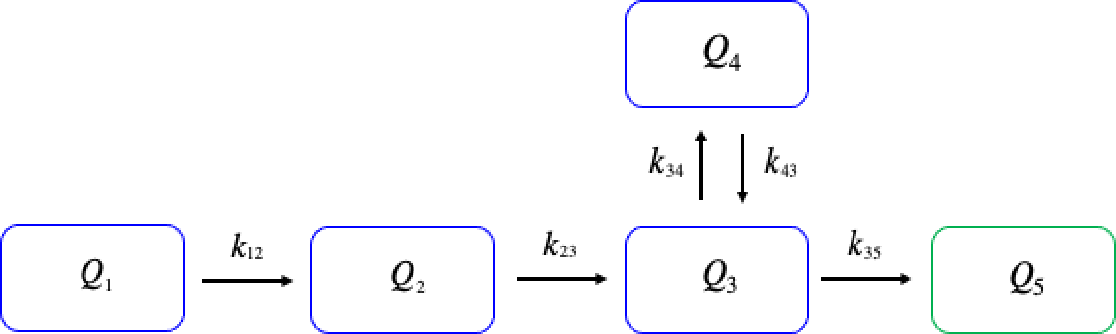
On travaille avec tous les compartiments sans exception.Il faut un modèle éprouvé par la pharmacocinétique de population.Il faut récupérer les microconstantes.Le mieux c'est de prendre au départ celles évaluées par Jelliffe.On comprend l'utilité des quantités au lieu des concentrations.On jauge l'avantage des quantités sur les concentrations.On voit très bien combien de temps il faut pour éliminer totalement le médicament.On visualise sans difficulté le temps d'élimination du médicament de l'organisme quelles que soient les conditions initiales de tous les compartiments.​
Le modèle
Q
1
est le comprimé ou le support de la dose administrée ou fraction disponible.​
Q
2
est le compartiment d'absorption de la fraction disponible.​
Q
3
est le sang ou le compartiment central.​
Q
4
est les tissus ou le compartiment périphérique ou profond.​
Q
5
est l'urine ou le compartiment d'élimination rénale.​Il faut être attentif au fait que ce modèle impose que les solutions de l’espace d’états soient des quantités dans les compartiments mais des débits dans les sorties.
LES VARIABLES D'ETAT
dx
1
dt
=-
k
12
x
1
​​
dx
2
dt
=
k
12
x
1
-
k
23
x
2
​​
dx
3
dt
=
k
23
x
2
-
k
34
x
3
-
k
35
x
3
+
k
43
x
4
​​
dx
4
dt
=
k
34
x
3
-
k
43
x
4
​​
dx
5
dt
=
k
35
x
3
LES SORTIES
y
1
=
k
35
x
3
LA MATRICE D'UN ESPACE D'ETATS

x
(t)=Ax(t)+Bf(t)
y(t)=Cx(t)+Df(t)
La matrice B fixe les signaux d’entrée qui s’ajoutent aux conditions initiales entrées séparément.La matrice D fixe l'approvisionnement direct du signal de sortie.Les matrices C et D sont évidemment inutiles ou entièrement égales à 0 quand toutes les sorties sont traitées comme des compartiments.
ATTENTION A LA PEDAGOGIE DE CET EXEMPLE
Pour exploiter la totalité de l’écriture en espace d’états, nous avons ajouté une quantité de 1 dans Q1 avec la fonction de Dirac (matrice B). En revanche, nous n’avons ajouté aucune sortie directe donc la matrice D reste entièrement égale à 0.​Donc, on peut à la fin mettre la matrice B entièrement à zéro pour revenir strictement au modèle ci-dessus et comparer les situations. On peut tout aussi bien faire varier les valeurs des matrices B et C et voir le retentissement sur les quantités présentes dans les compartiments et surtout sur l’élimination. L’enjeu de la distribution d’un médicament étant non seulement de savoir quelle quantité est présente dans chaque compartiment mais aussi de savoir si le médicament est totalement éliminé par le foie et/ou l’urine selon le cas.​
StateResponse
matriceDigitoA=
-
k
12
0
0
0
k
12
-
k
23
0
0
0
k
23
-(
k
34
+
k
35
)
k
43
0
0
k
34
-
k
43
{{-
k
12
,0,0,0},{
k
12
,-
k
23
,0,0},{0,
k
23
,-
k
34
-
k
35
,
k
43
},{0,0,
k
34
,-
k
43
}}
matriceDigitoB=
1
0
0
0
{{1},{0},{0},{0}}
matriceDigitoC=(
0
0
k
35
0
)
{{0,0,
k
35
,0}}
matriceDigitoD=(
0
)
Les conditions initiales :
OutputResponse
Les conditions initiales :
On a donné 250. On retrouve bien 250 dans l’urine. Tout est éliminé dans l’urine.