Piston Equations of Motion

CCN Studios@FreeFromCreations
© 2012-Present CCN Studios​
Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International Public License
​
​
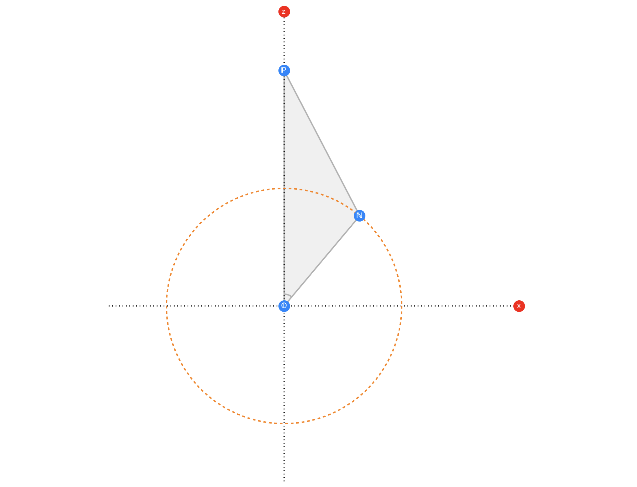
By Law of Cosines establish an equation between the length of line 𝕆ℕ namely r radius for crank
and length of line   namely z coordinate for piston and length of line  namely ℓ and Cosine of
angle between the lines   and  namely θ = ∠  .
​
● Solve the equation for z(θ) as a function of angle θ
● Set θ(t) = ωt as a linear function of time
● Increment t ⟶ t + Δt for each step of the animation loop

Compute the Law of Cosines for θ = ∠  

● Set piston initial position at (0,0,z) ● Piston is bound only to move vertically up or down● Compute the dot product

.

In[]:=
Pv={0,0,z}​​Nv=r*{Sin[θ],0,Cos[θ]}​​​​(*computethedotproduct.*)​​dot2=(Pv-Nv).(Pv-Nv)​​​​
Out[]=
{0,0,z}
Out[]=
{rSin[θ],0,rCos[θ]}
Out[]=
2
(z-rCos[θ])
+
2
r
2
Sin[θ]

Expand and Simplify

.


In[]:=
Expand[dot2]
Out[]=
2
z
-2rzCos[θ]+
2
r
2
Cos[θ]
+
2
r
2
Sin[θ]
In[]:=
rhs=Simplify@Expand[dot2]
Out[]=
2
r
+
2
z
-2rzCos[θ]
In[]:=
Simplify@Expand[Norm[(Pv-Nv)]^2/.{Abs->Identity}]===rhs
Out[]=
True

Solve the Law of Cosines for z

In[]:=
Solve[l^2==r^2+z^2-2*r*z*Cos[θ]&&z>0&&l>2*r&&r>0&&l>0,{z},Reals]
Out[]=
z
rCos[θ]+
2
l
-
2
r
+
2
r
2
Cos[θ]
if r>0&&l>2r

Make a new function pistonz [r ,l , θ] which outputs 
In[]:=
pistonz[r_,l_,θ_]:={0,0,r*Cos[θ]+Sqrt[l^2-r^2*Sin[θ]^2]};
In[]:=
pistonz[r,l,θ]
Out[]=
0,0,rCos[θ]+
2
l
-
2
r
2
Sin[θ]


Check the length of pistonz [r ,l , θ] vector is always l

In[]:=
SquaredEuclideanDistance[pistonz[r,l,θ],r*{Sin[θ],0,Cos[θ]}]/.{Abs->Identity}
Out[]=
2
l

Compute the speed of the Piston

In[]:=
D[pistonz[r,l,θ],θ]
Out[]=
0,0,-rSin[θ]-
2
r
Cos[θ]Sin[θ]
2
l
-
2
r
2
Sin[θ]


Compute the acceleration of the Piston

In[]:=
D[pistonz[r,l,θ],{θ,2}]
Out[]=
0,0,-rCos[θ]-
4
r
2
Cos[θ]
2
Sin[θ]
3/2
(
2
l
-
2
r
2
Sin[θ]
)
-
2
r
2
Cos[θ]
2
l
-
2
r
2
Sin[θ]
+
2
r
2
Sin[θ]
2
l
-
2
r
2
Sin[θ]


Compute the parametric path of the Piston as a function of time t

In[]:=
pistonz[r,l,θ]/.{θ->(ω*t)}
Out[]=
0,0,rCos[tω]+
2
l
-
2
r
2
Sin[tω]


Compute z(0)

In[]:=
FullSimplify[PowerExpand@(pistonz[r,l,ω*t]/.{t->0})]
Out[]=
{0,0,l+r}

Compute  as function of θ

In[]:=
vN[θ_]=r*{Sin[θ],0,Cos[θ]};
In[]:=
PN=vN[θ]-pistonz[r,l,θ]
Out[]=
rSin[θ],0,-
2
l
-
2
r
2
Sin[θ]

In[]:=
dot=PN.({0,0,0}-pistonz[r,l,θ])
Out[]=
-
2
l
-
2
r
2
Sin[θ]
-rCos[θ]-
2
l
-
2
r
2
Sin[θ]


Compute Angle ∠ 

Dot product of pistonz[r,l,θ] vector and  divide by their corresponding norms is the Cos( )
In[]:=
PowerExpand[dot/(Norm[PN]*Norm[{0,0,0}-pistonz[r,l,θ]])/.{Abs->Identity}]
Out[]=
-
2
l
-
2
r
2
Sin[θ]
l

Compute Angle ∠ 

In[]:=
NP=-vN[θ]+pistonz[r,l,θ]​​NO={0,0,0}-vN[θ]
Out[]=
-rSin[θ],0,
2
l
-
2
r
2
Sin[θ]

Out[]=
{-rSin[θ],0,-rCos[θ]}
In[]:=
dot=NP.NO
Out[]=
2
r
2
Sin[θ]
-rCos[θ]
2
l
-
2
r
2
Sin[θ]