Constructions
A Euclidean construction consists of starting with a set of givens, such as segment AB, then adds arcs or circles with a compass and lines or segments with a straightedge. For example, two circles of radius AB centered on A and B can find an equidistant point C. Then segments AC and BC can be drawn for an equilateral triangle construction.
-
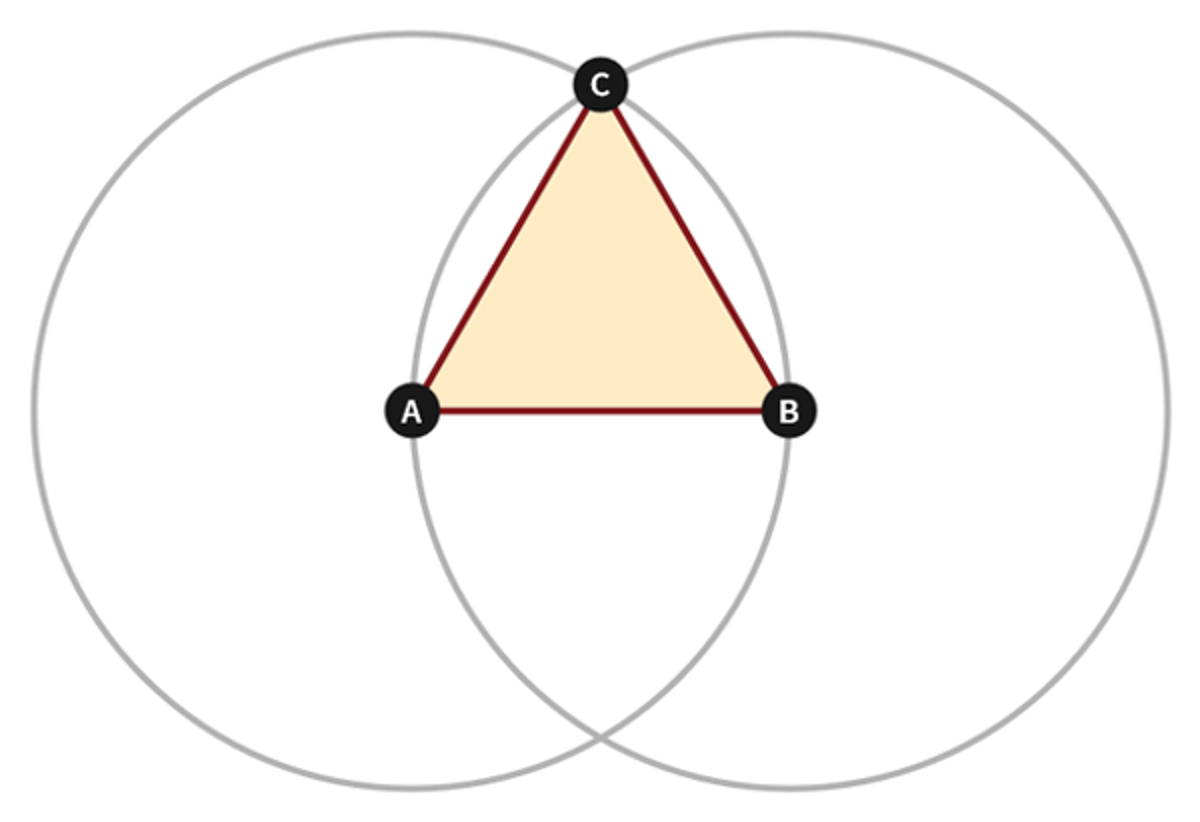
Euclid Book 1 Proposition 1
-
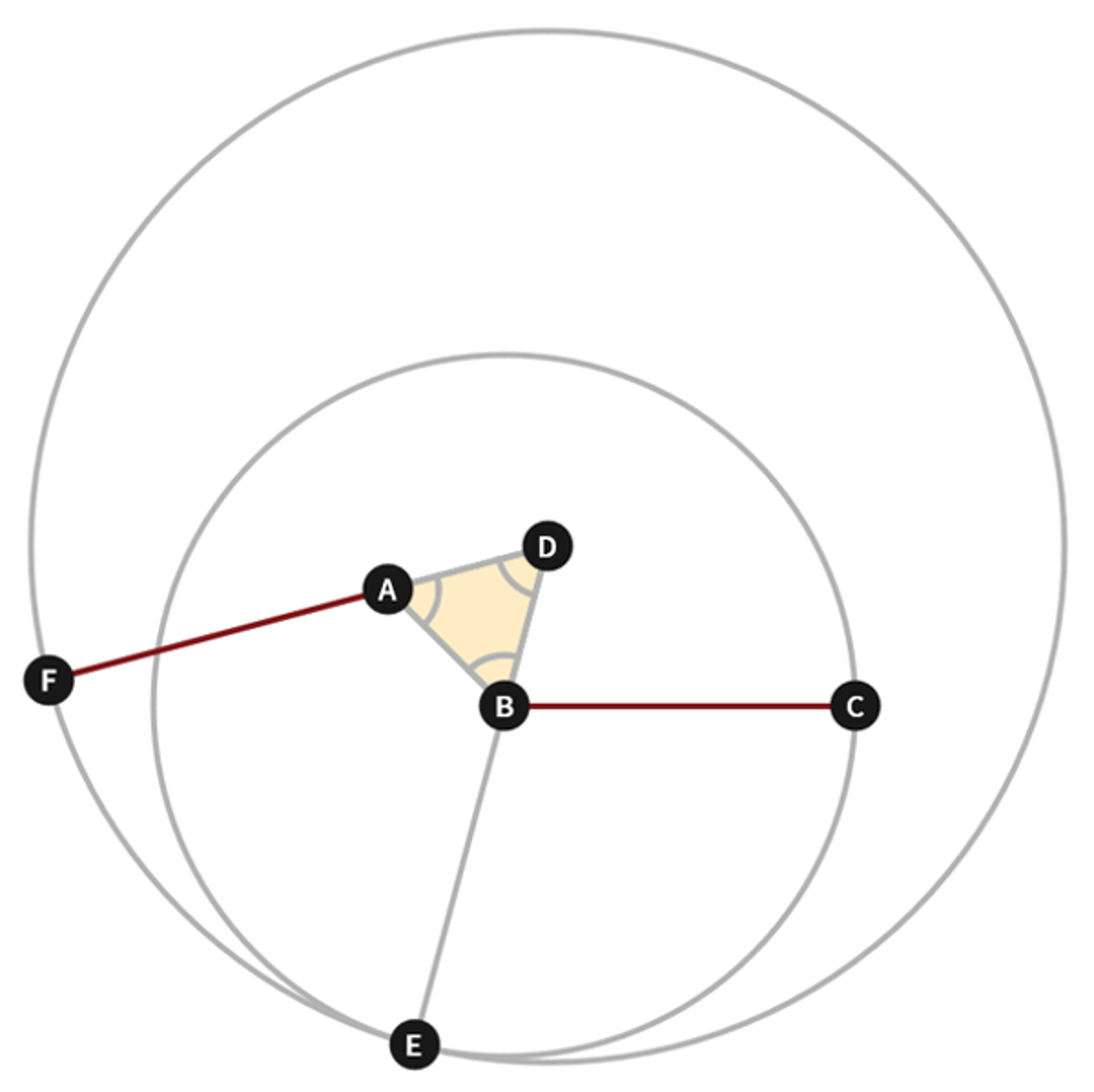
Euclid Book 1 Proposition 2
-
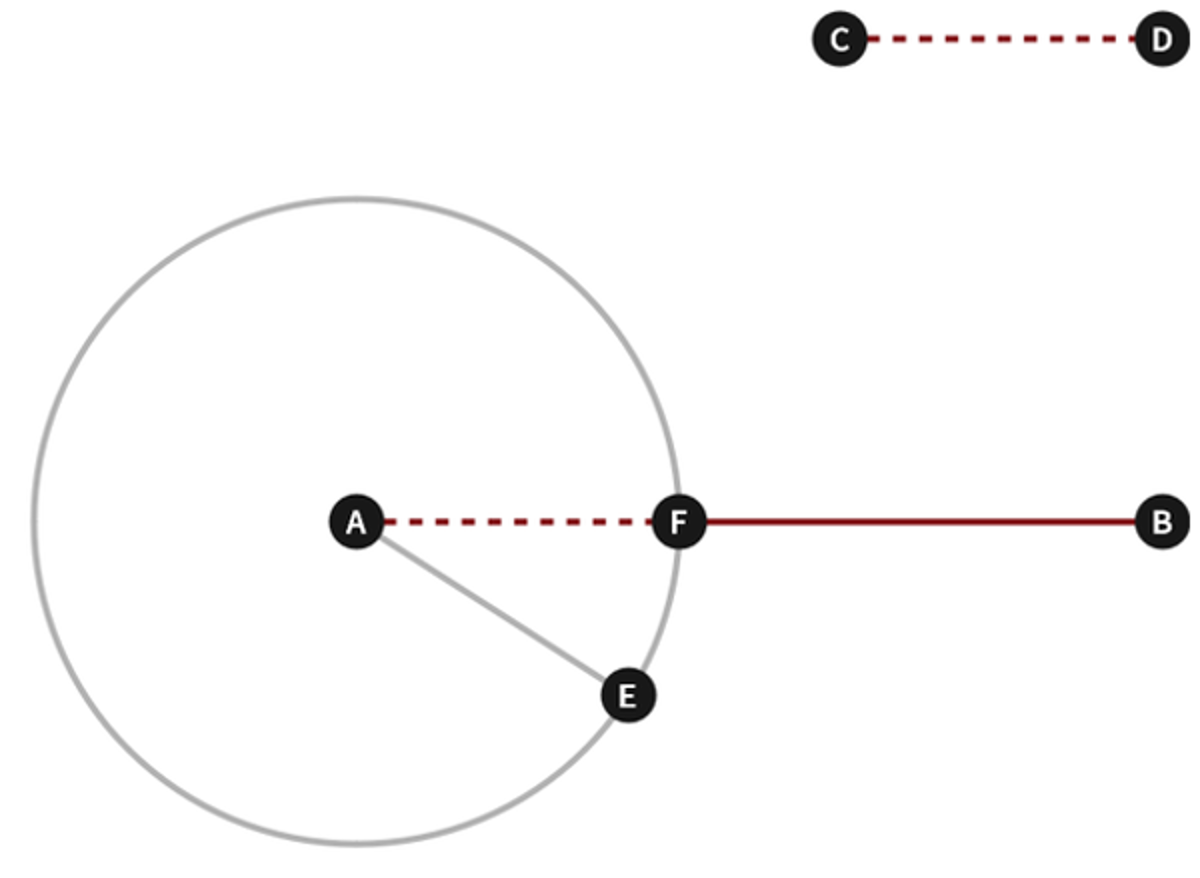
Euclid Book 1 Proposition 3
-
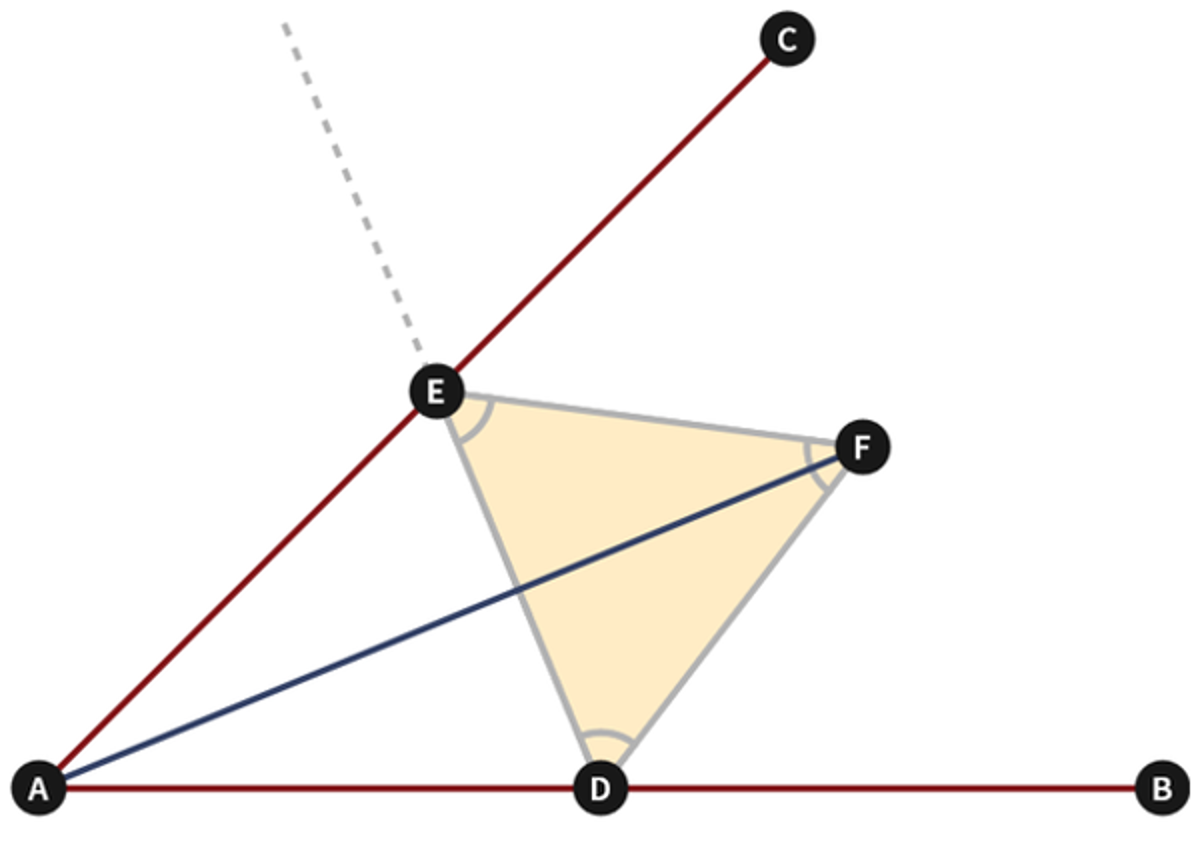
Euclid Book 1 Proposition 9
-
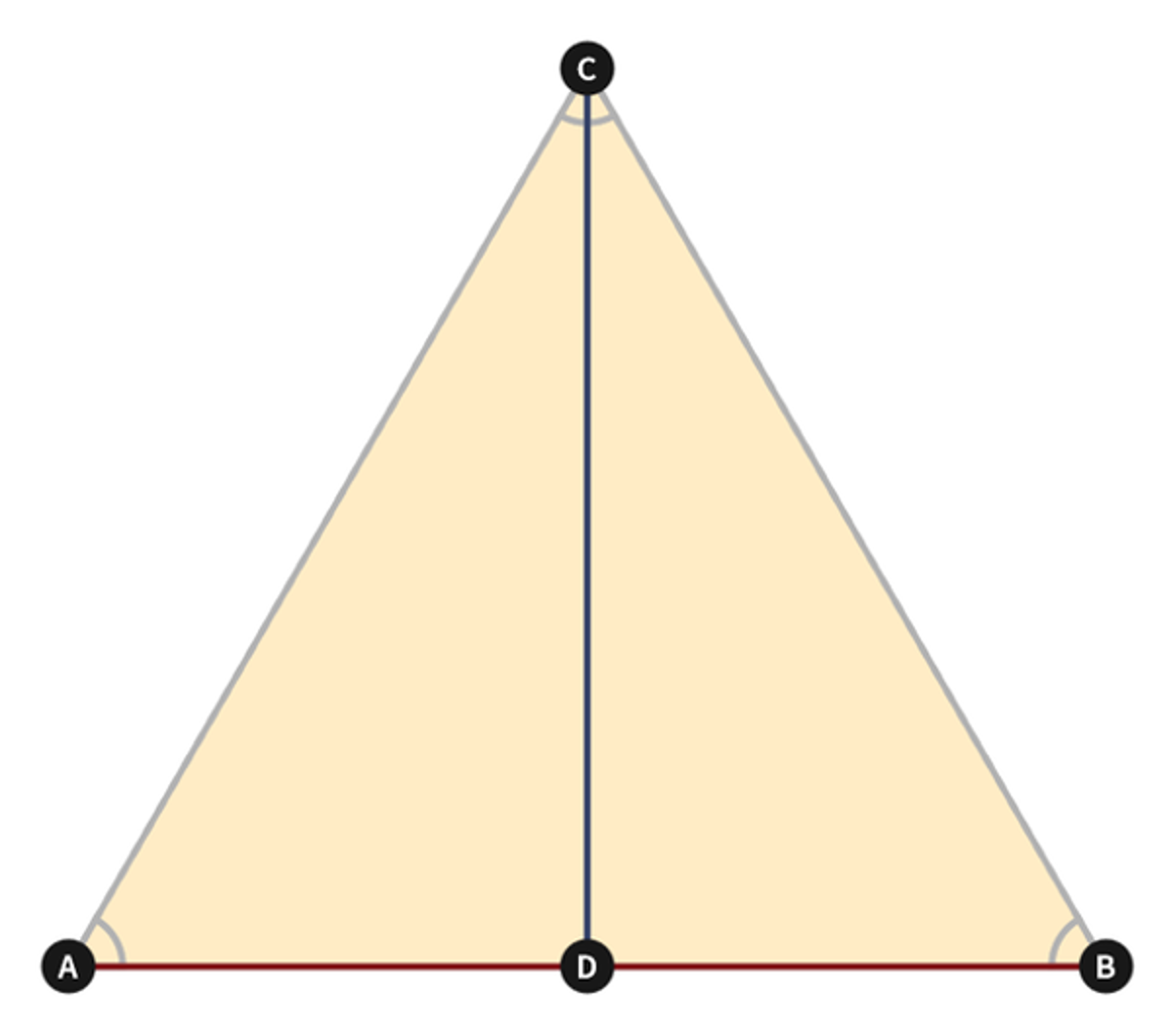
Euclid Book 1 Proposition 10
-
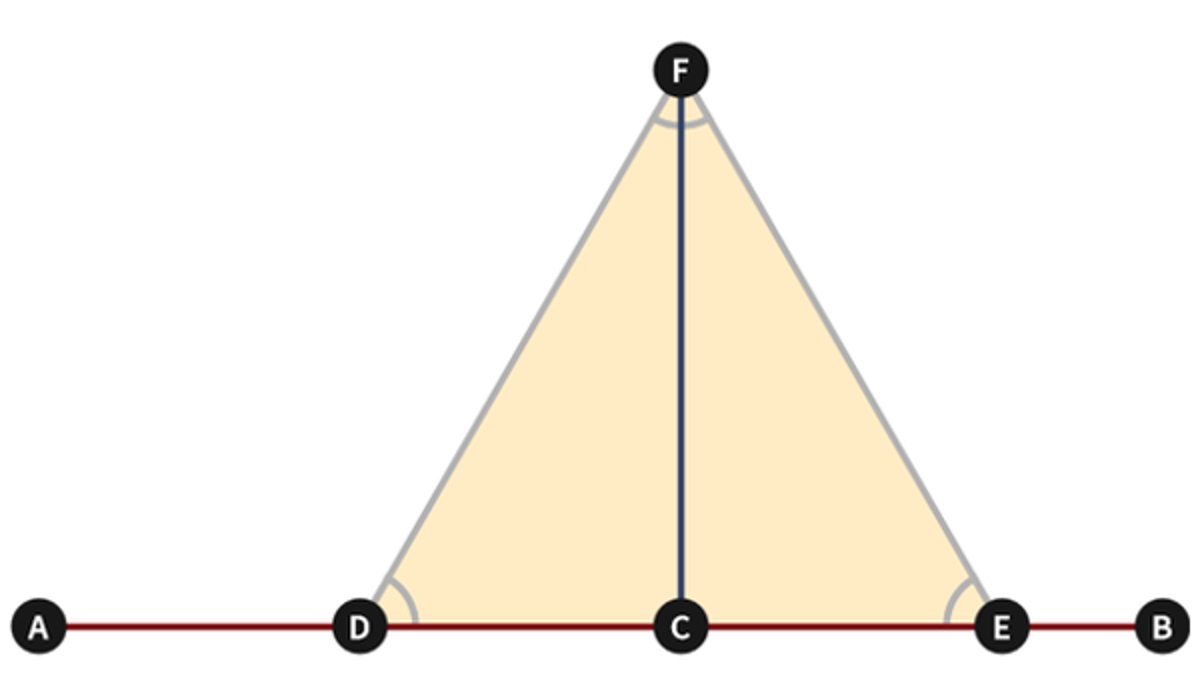
Euclid Book 1 Proposition 11
-
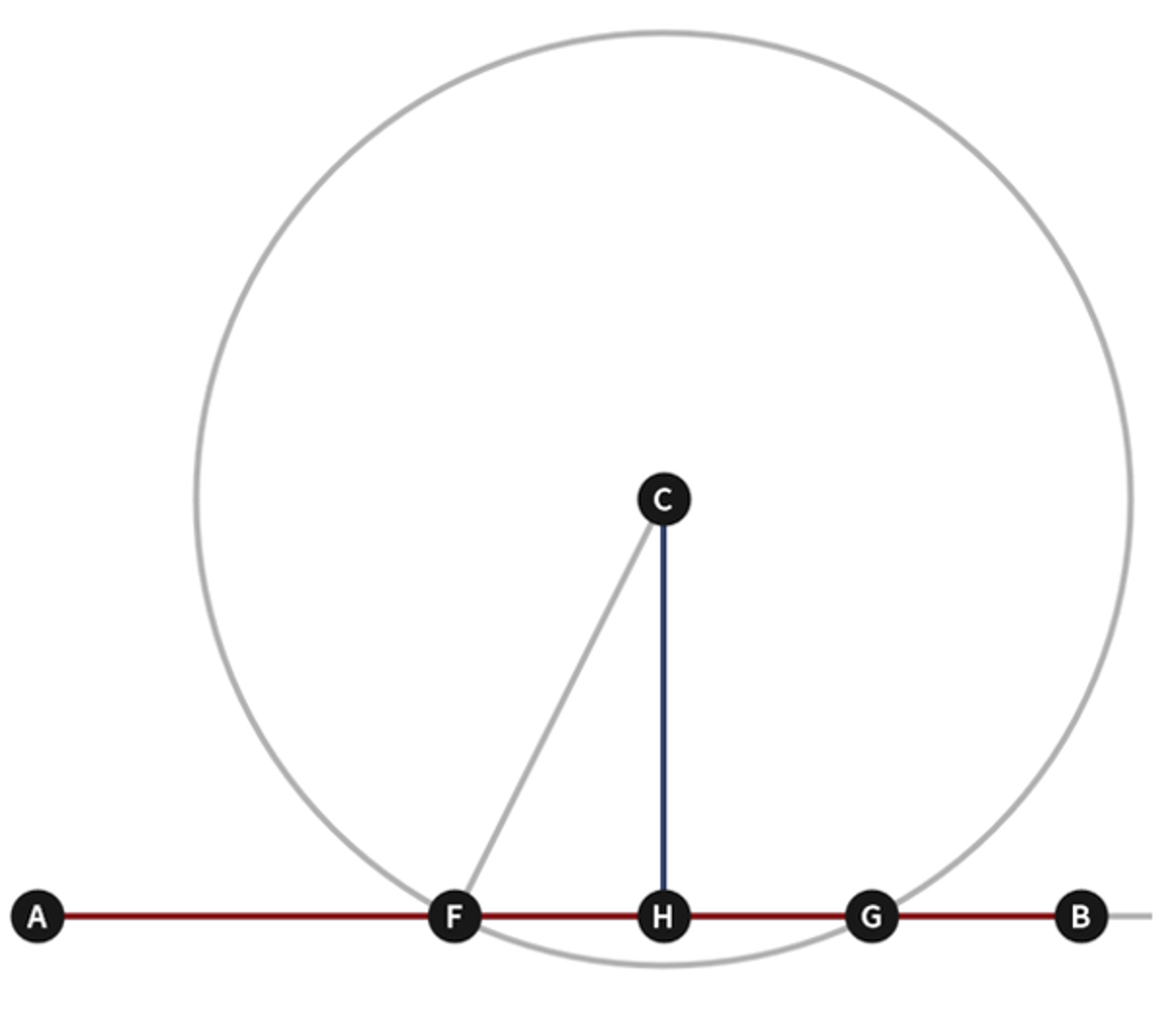
Euclid Book 1 Proposition 12
-
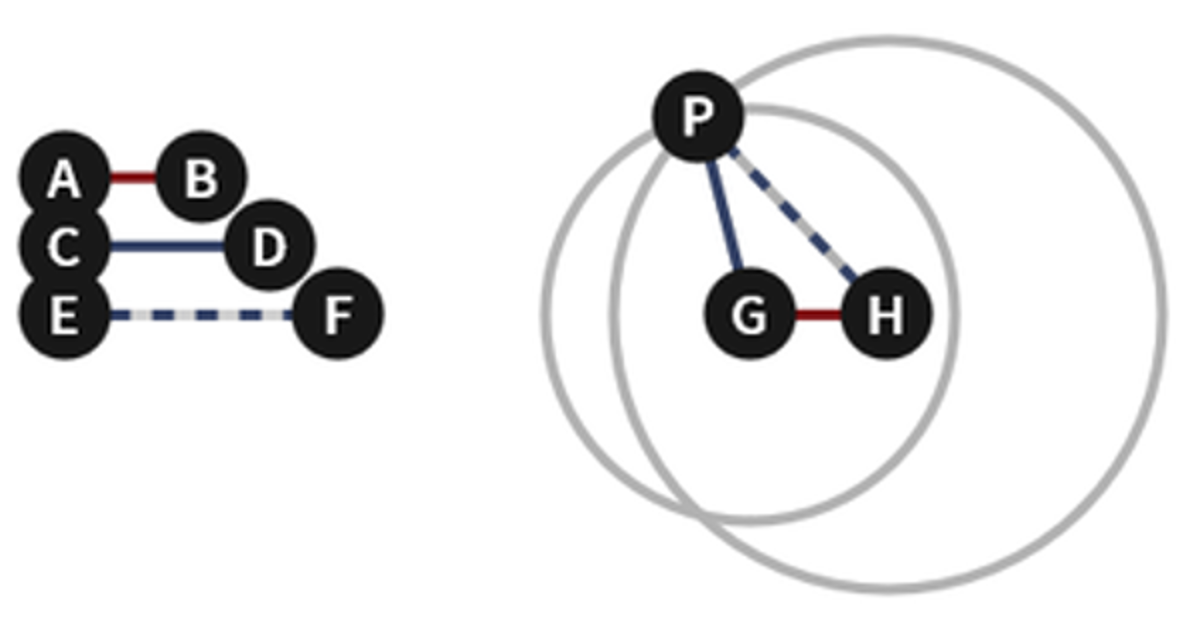
Euclid Book 1 Proposition 22
-
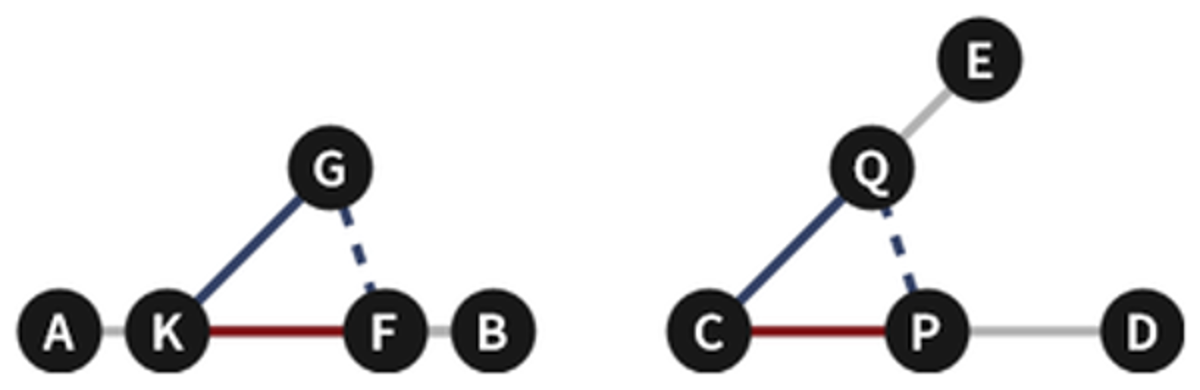
Euclid Book 1 Proposition 23
-
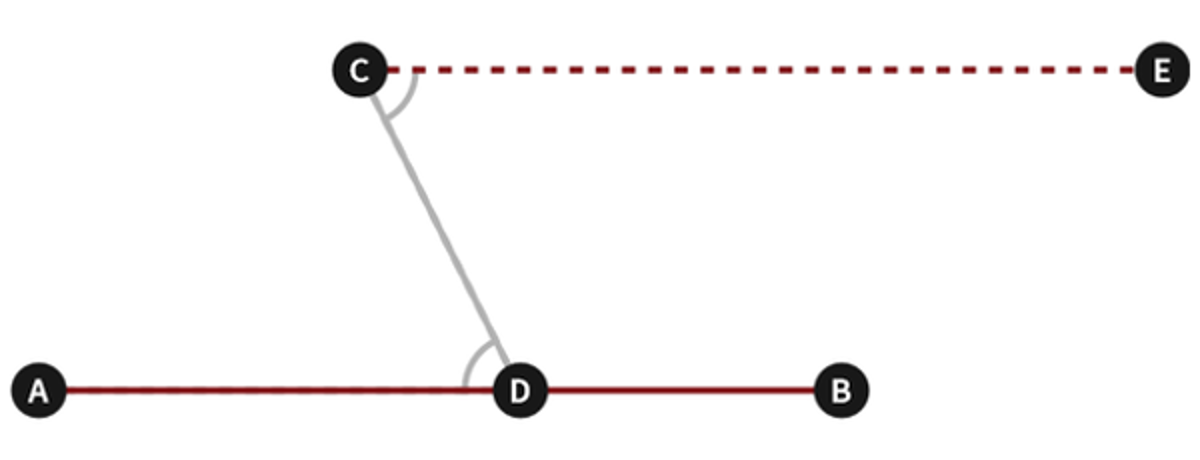
Euclid Book 1 Proposition 31
-
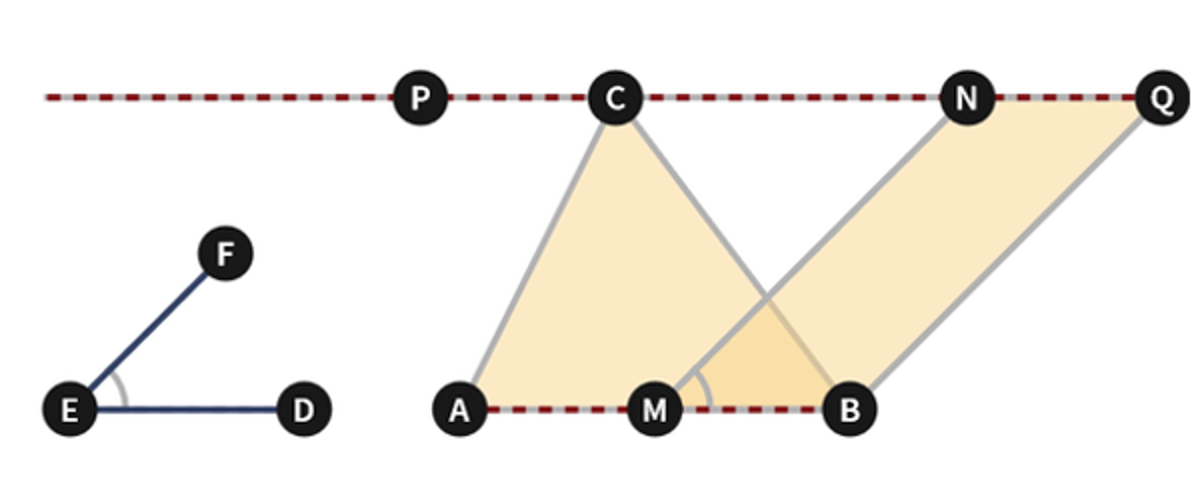
Euclid Book 1 Proposition 42
-
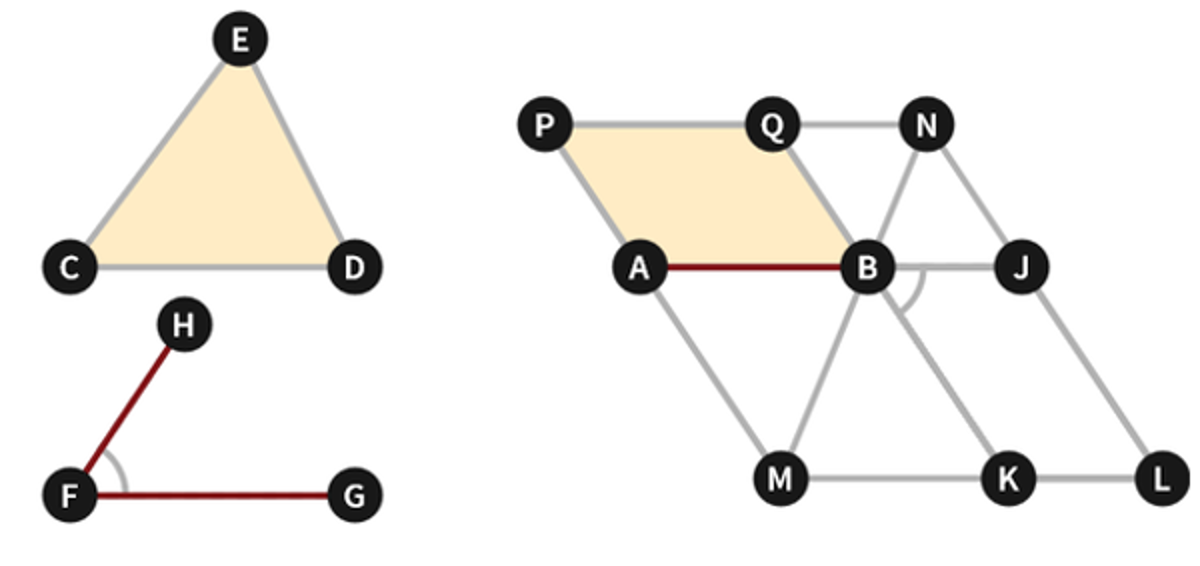
Euclid Book 1 Proposition 44
-
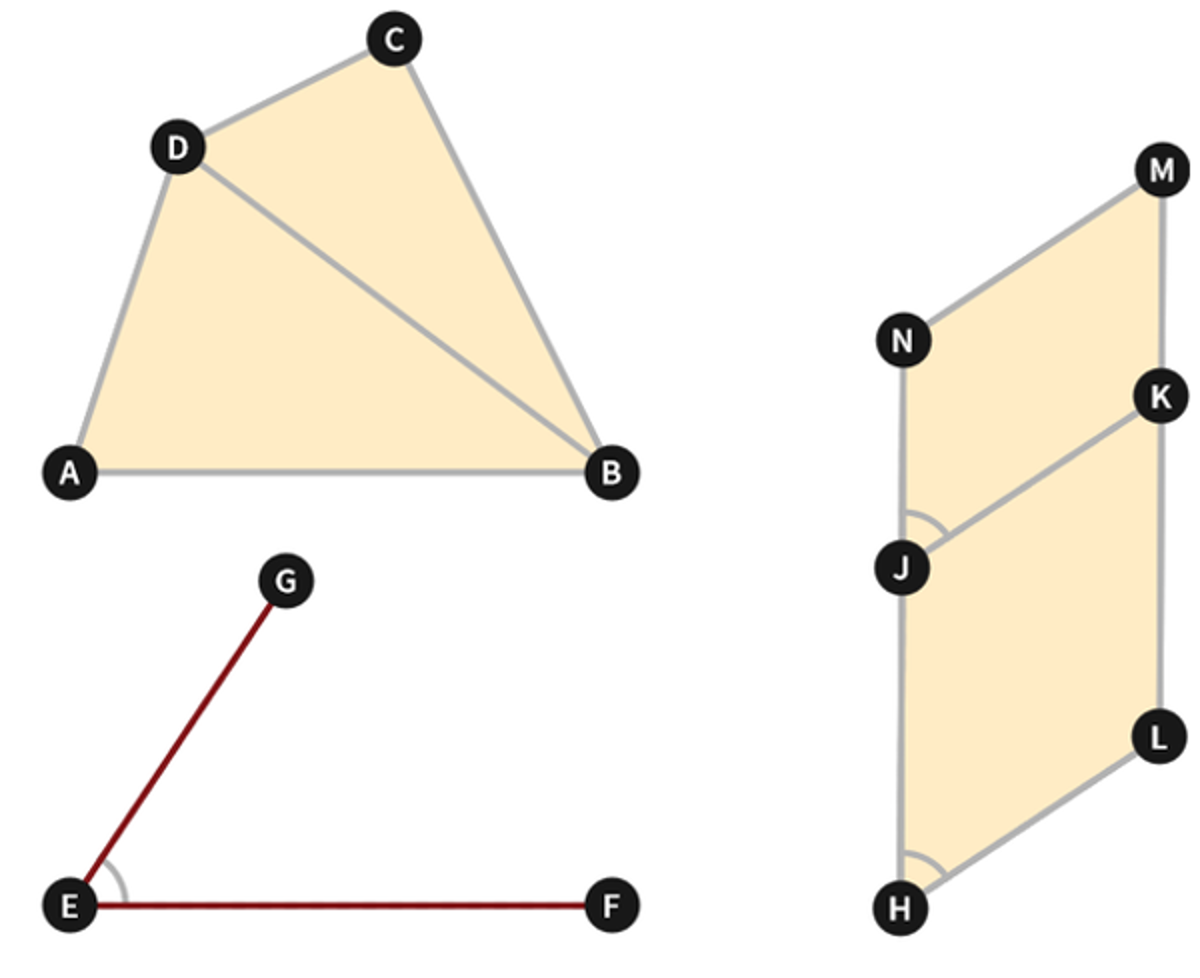
Euclid Book 1 Proposition 45
-
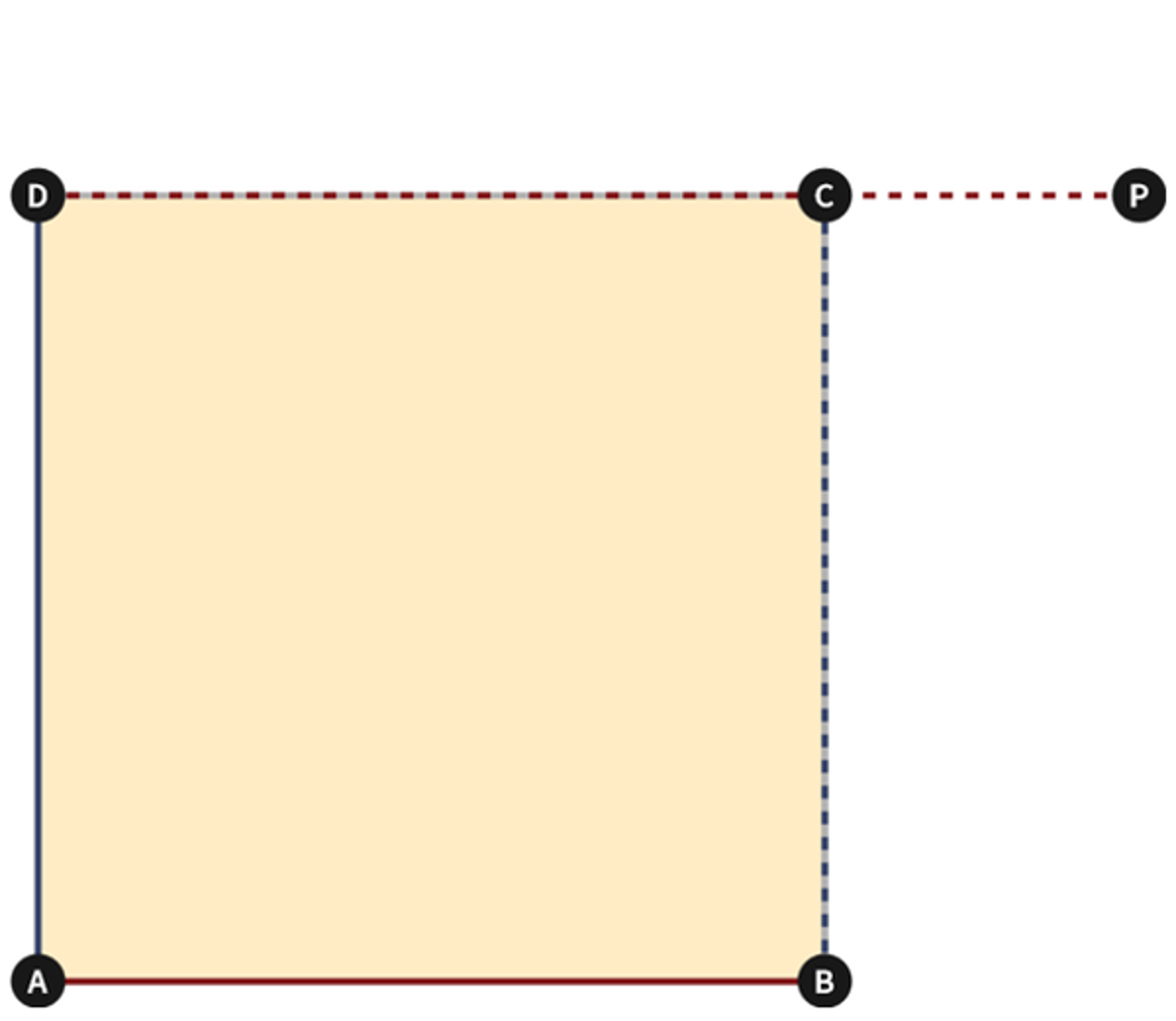
Euclid Book 1 Proposition 46
-
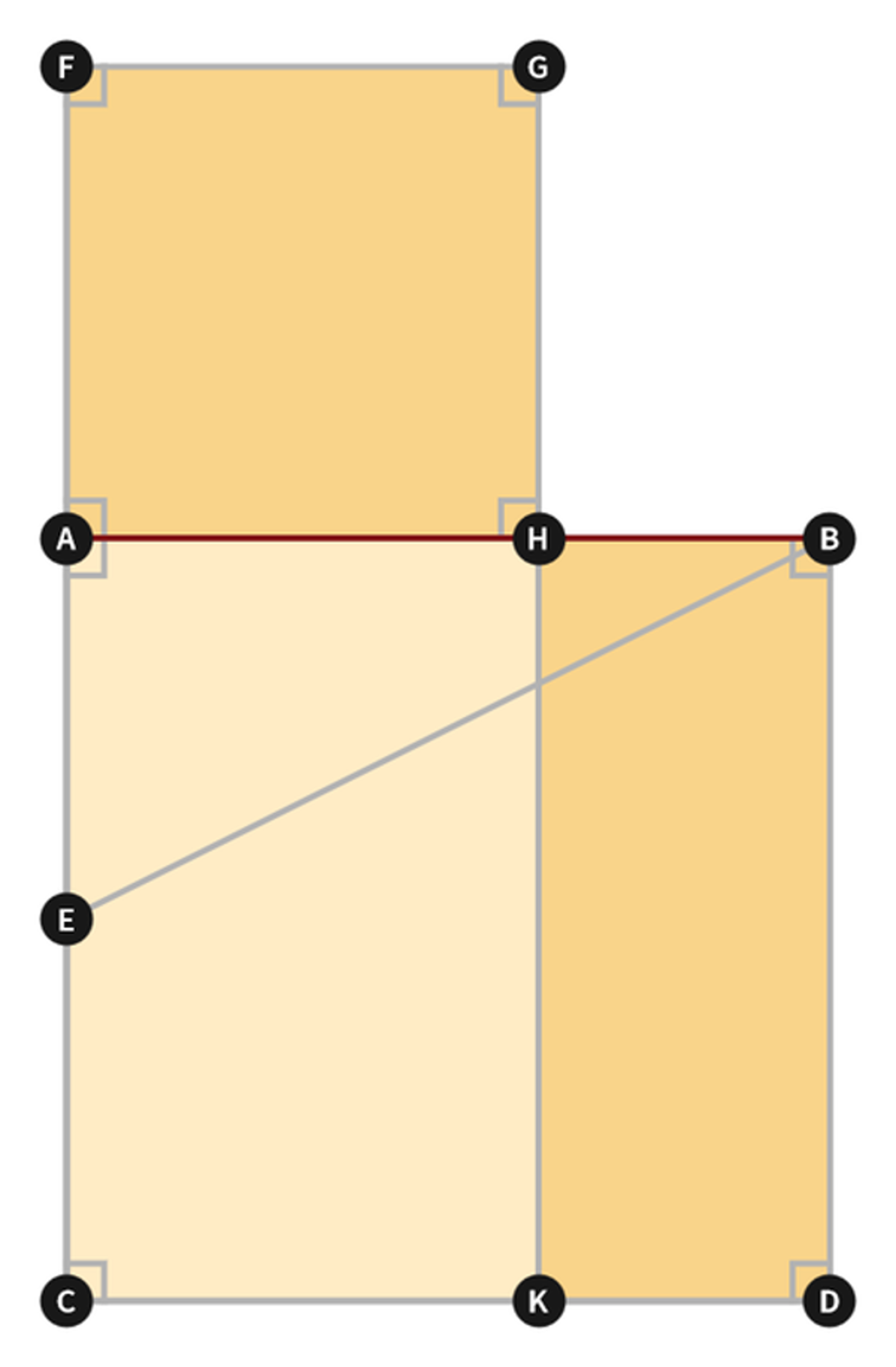
Euclid Book 2 Proposition 11
-
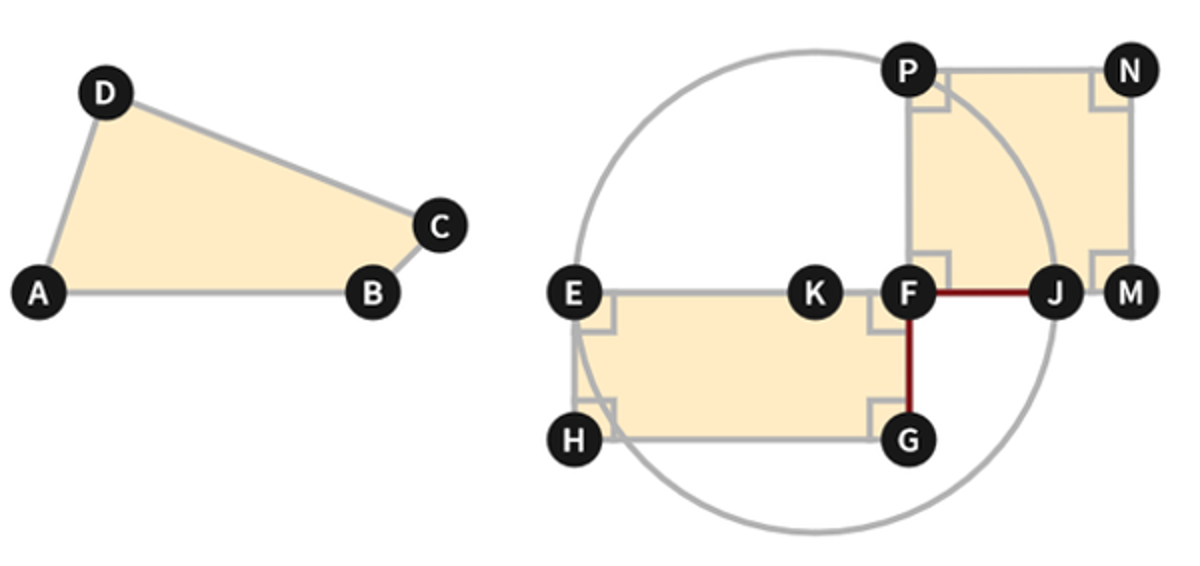
Euclid Book 2 Proposition 14
-
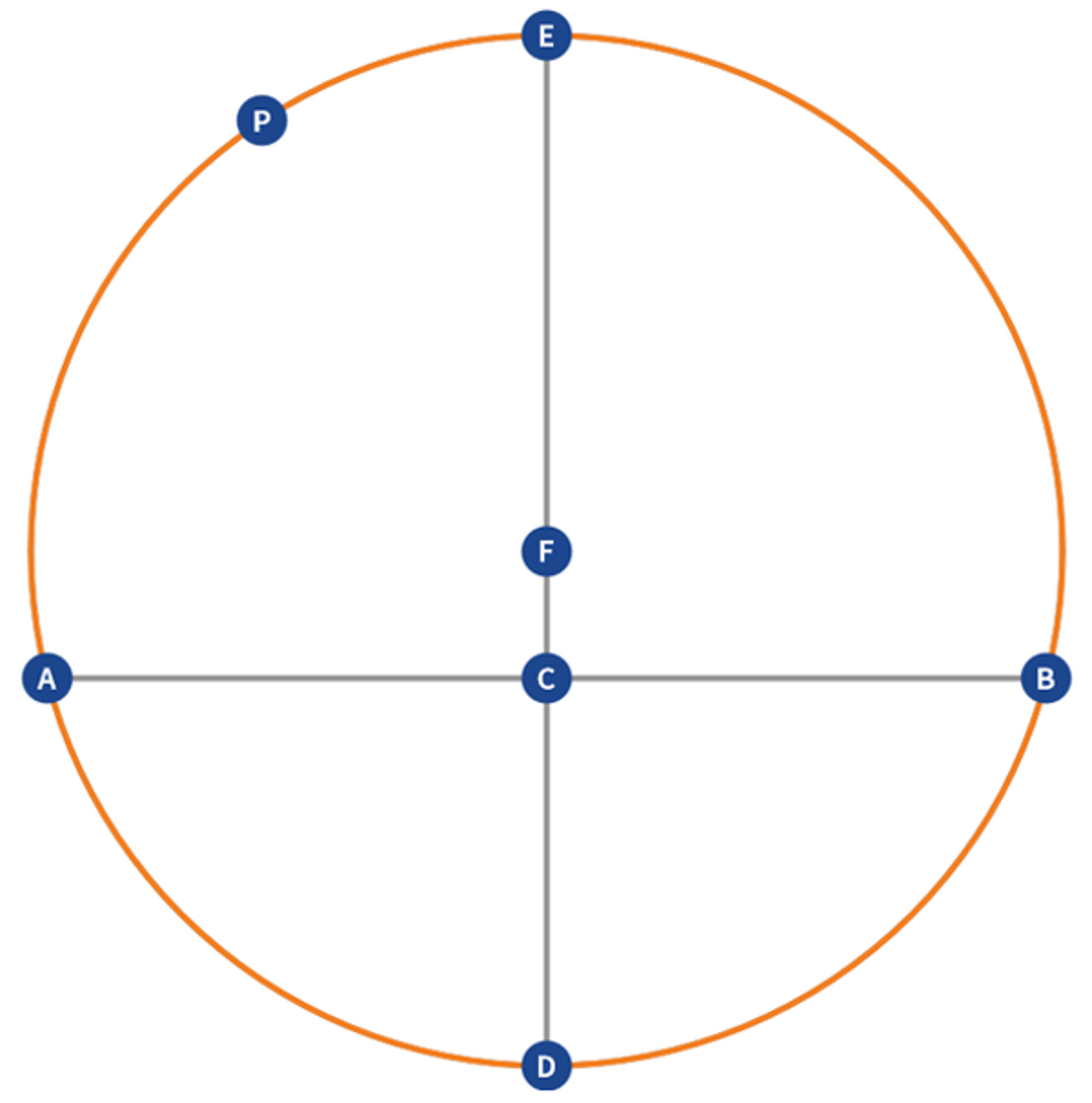
Euclid Book 3 Proposition 1
-
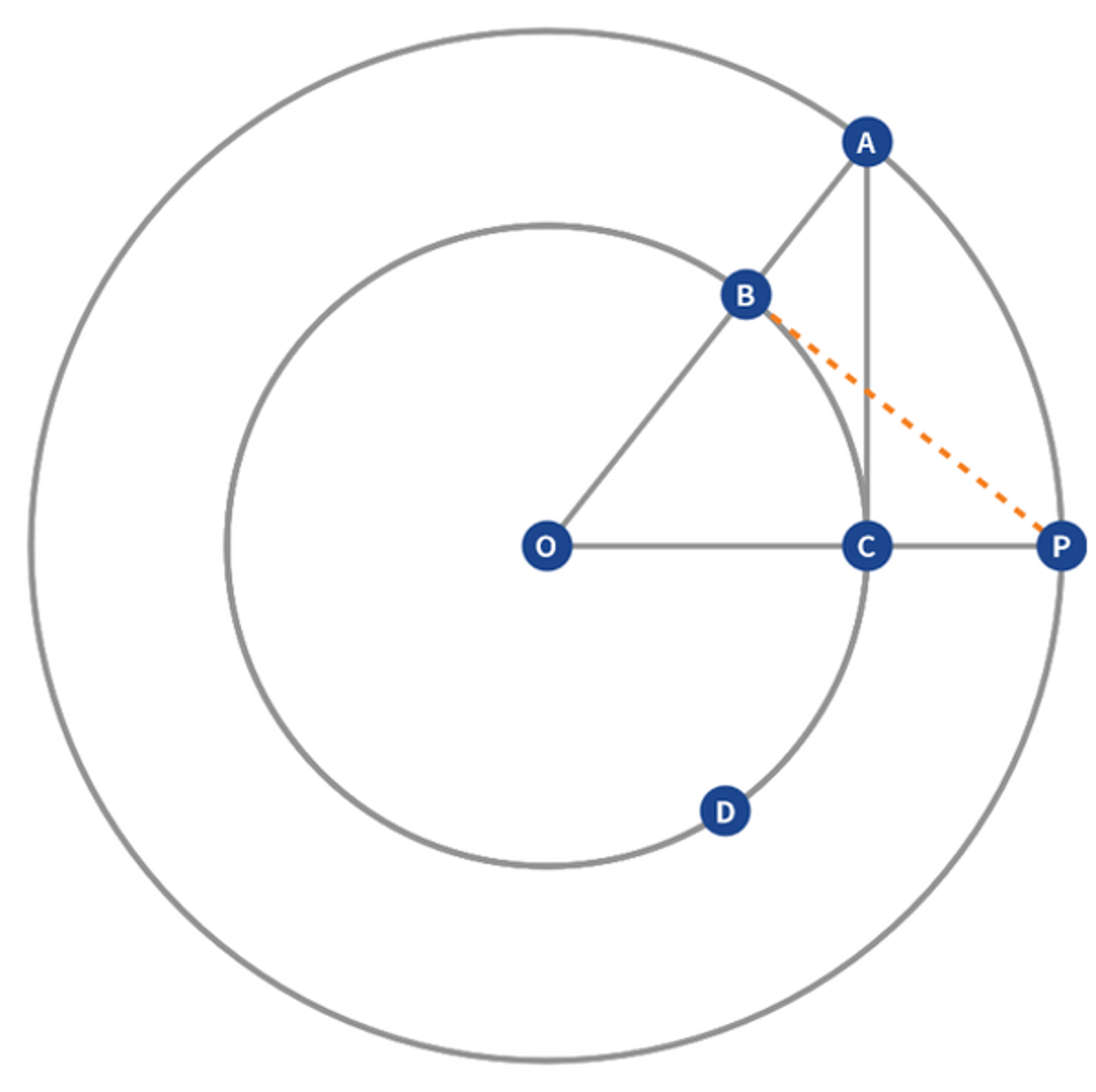
Euclid Book 3 Proposition 17
-
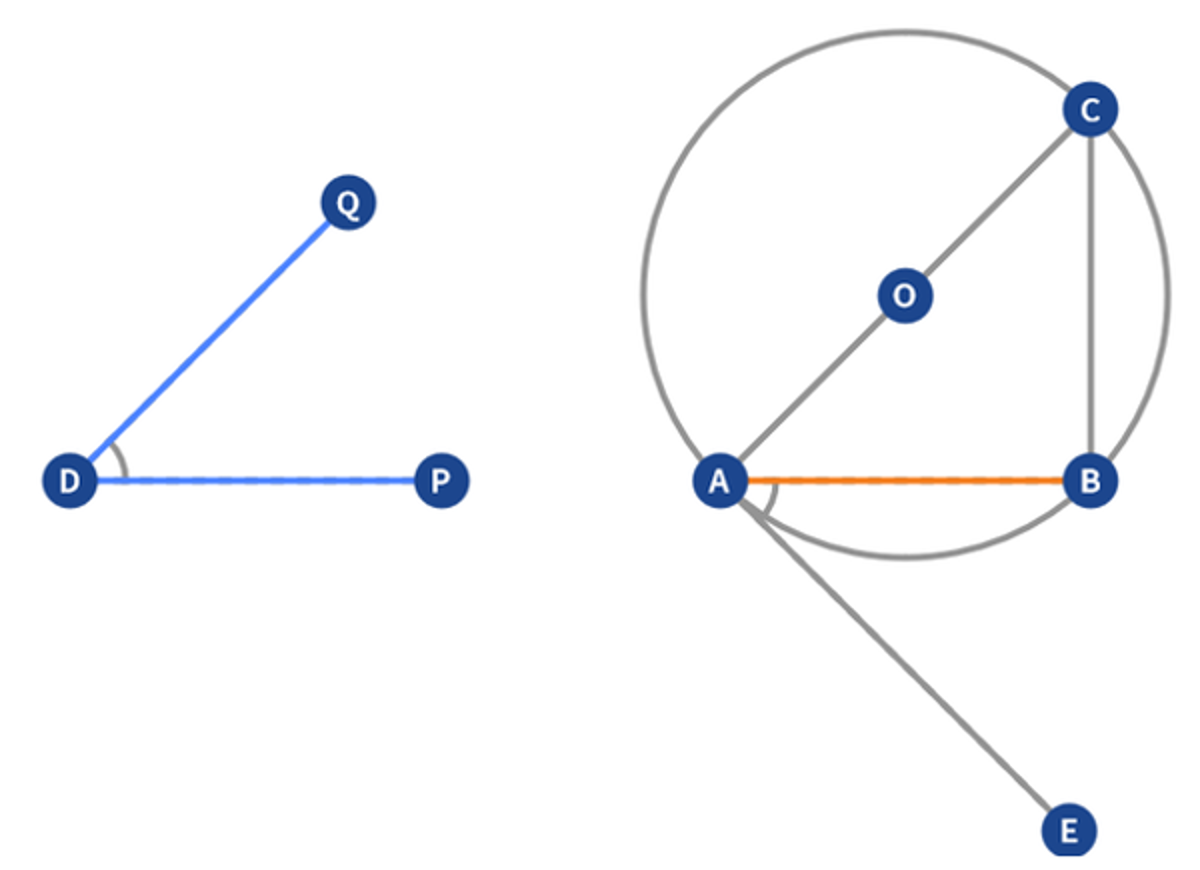
Euclid Book 3 Proposition 33
-
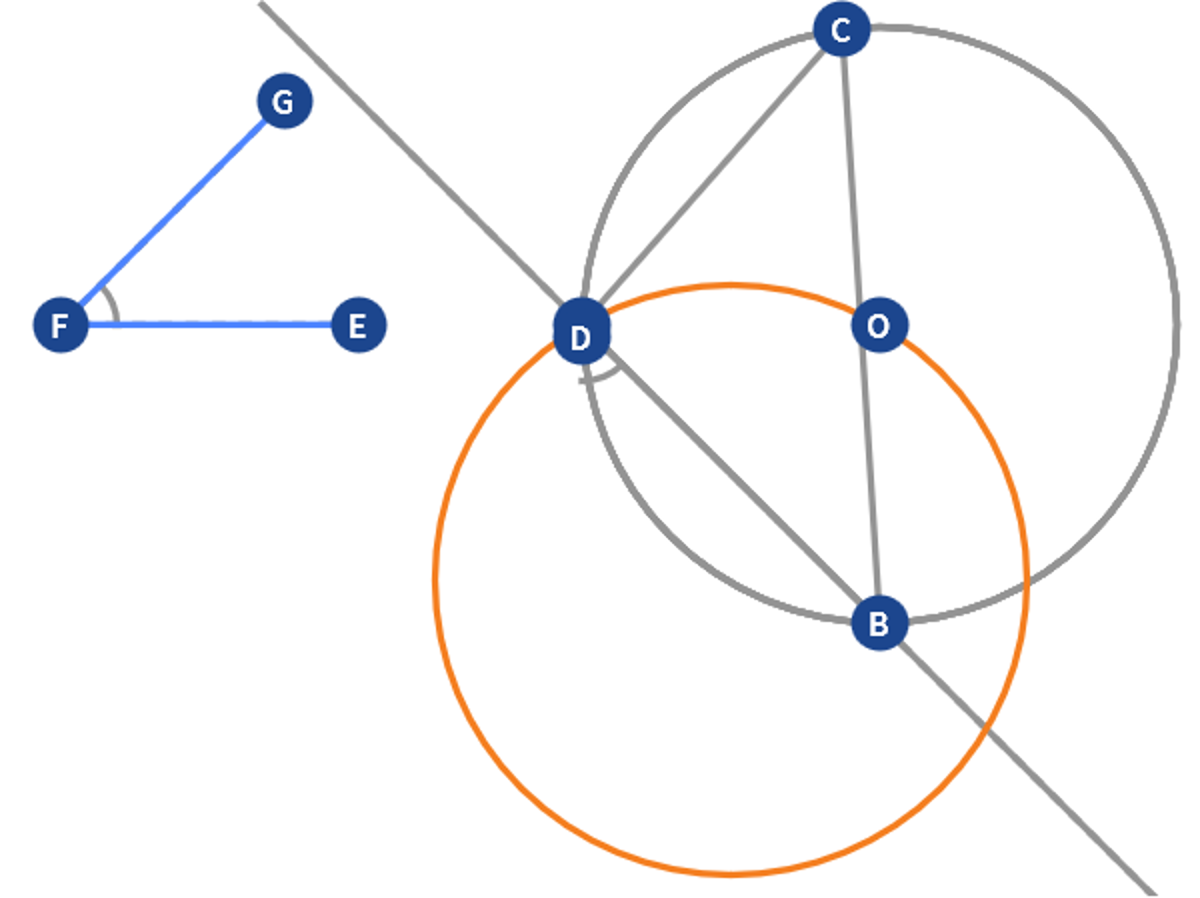
Euclid Book 3 Proposition 34
-
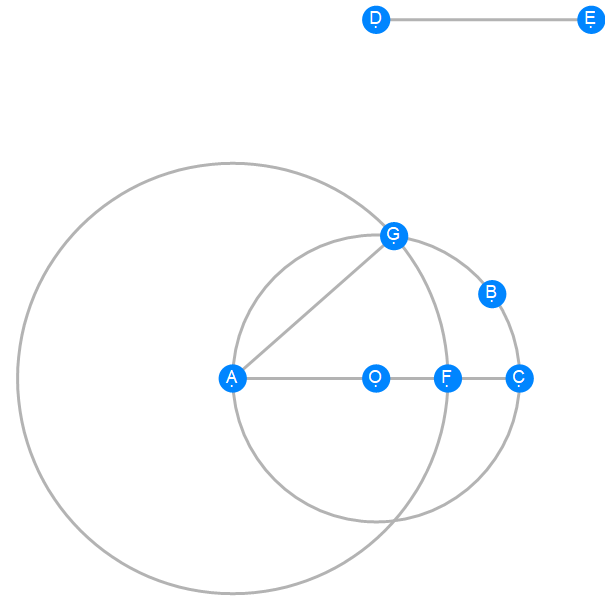
Euclid Book 4 Proposition 1
-
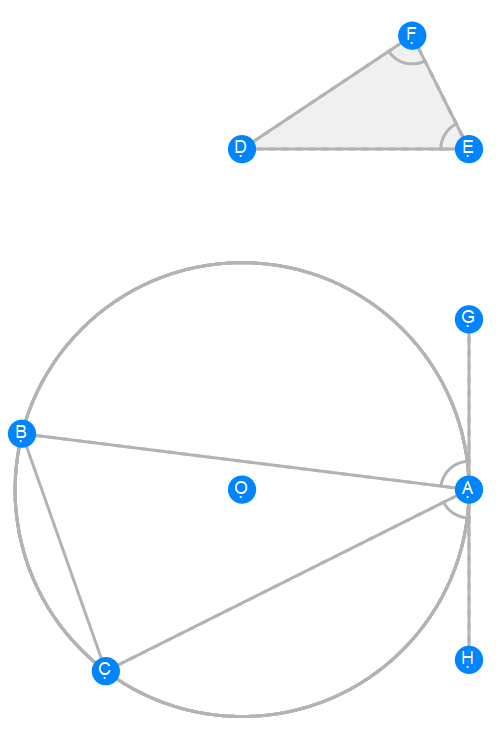
Euclid Book 4 Proposition 2
-
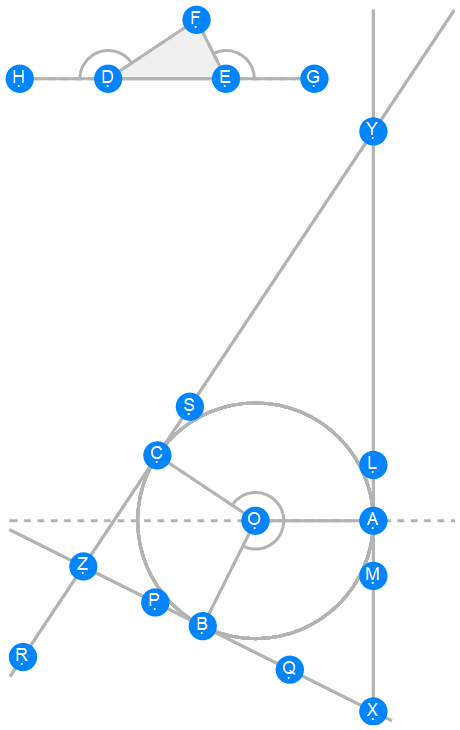
Euclid Book 4 Proposition 3
-
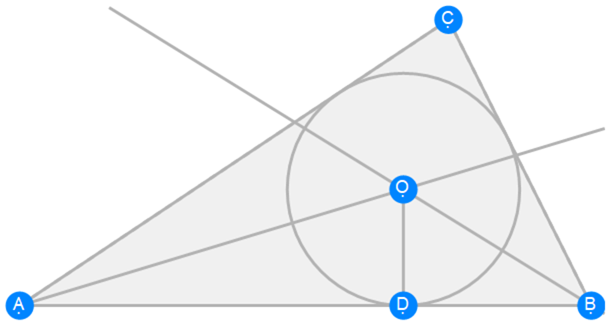
Euclid Book 4 Proposition 4
-
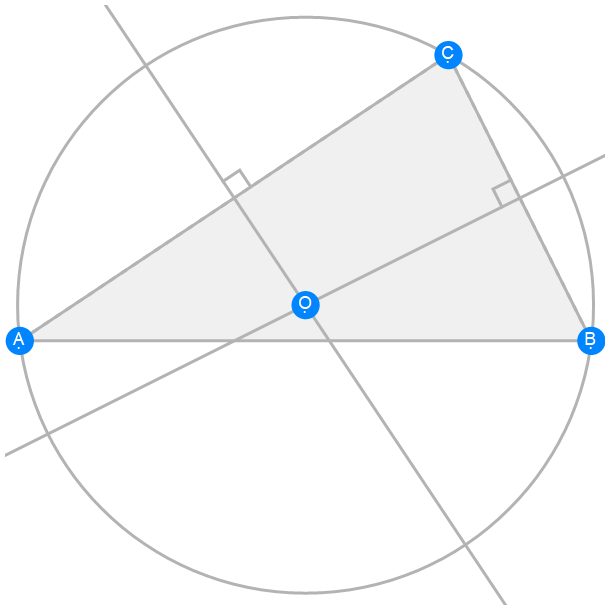
Euclid Book 4 Proposition 5
-

Euclid Book 4 Proposition 6
-
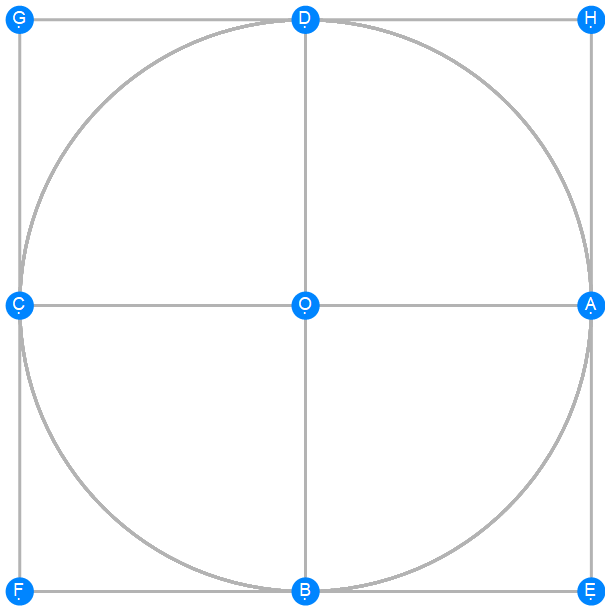
Euclid Book 4 Proposition 7
-
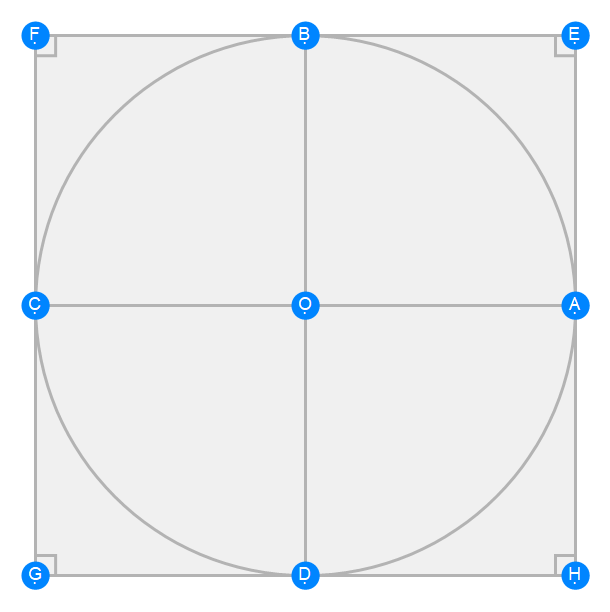
Euclid Book 4 Proposition 8
-
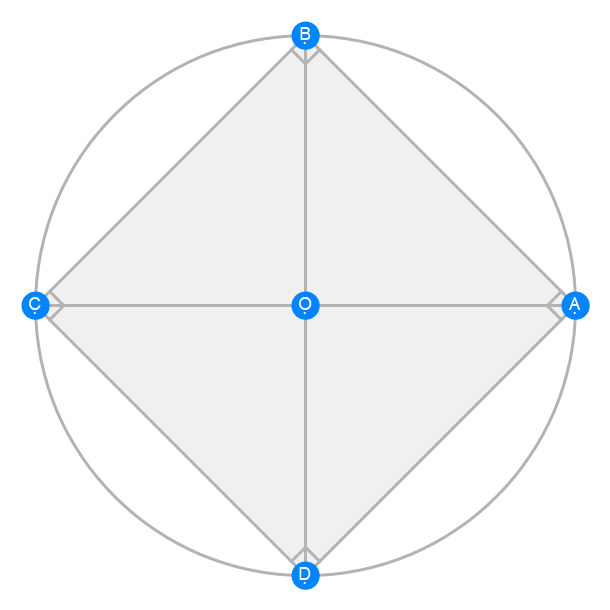
Euclid Book 4 Proposition 9
-
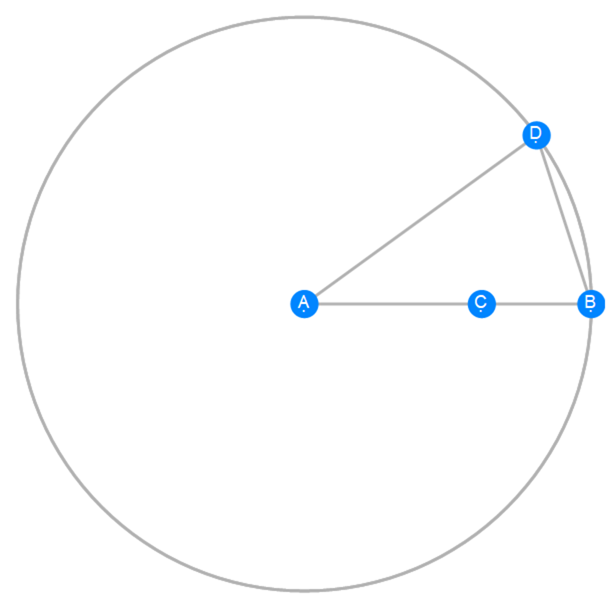
Euclid Book 4 Proposition 10
-
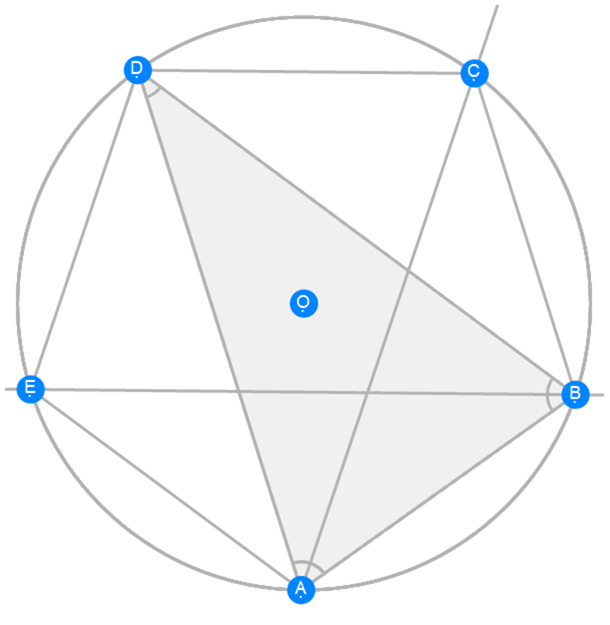
Euclid Book 4 Proposition 11
-
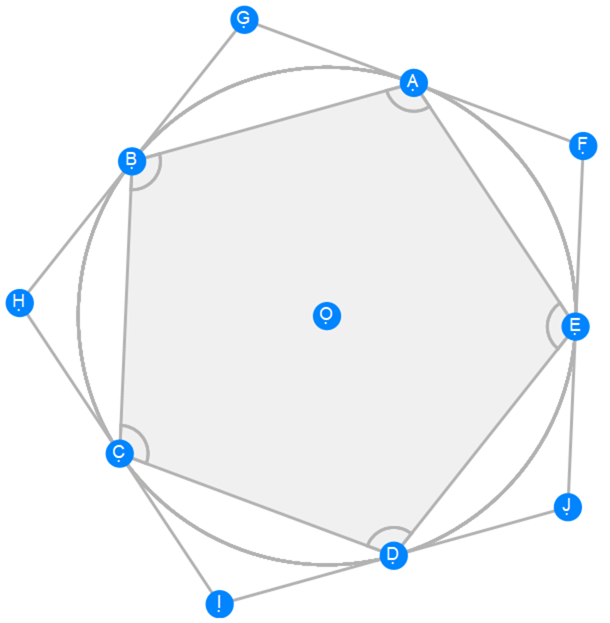
Euclid Book 4 Proposition 12
-
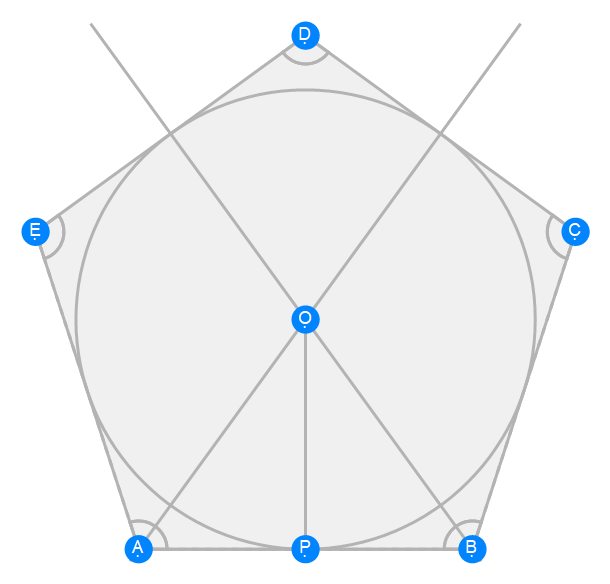
Euclid Book 4 Proposition 13
-
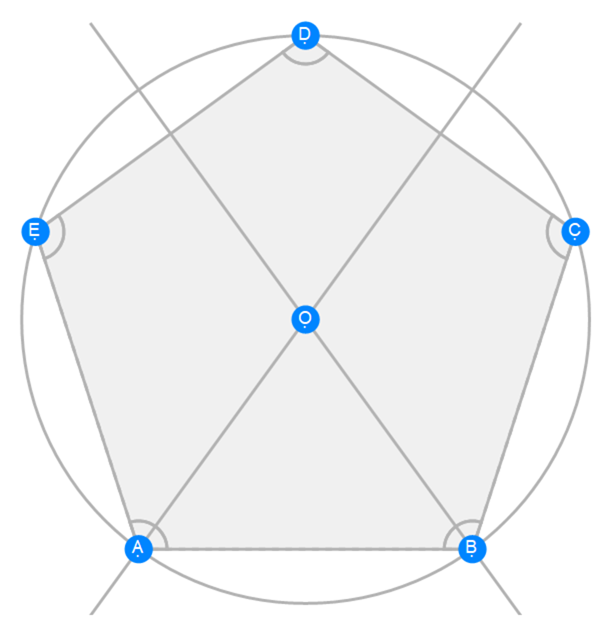
Euclid Book 4 Proposition 14
-
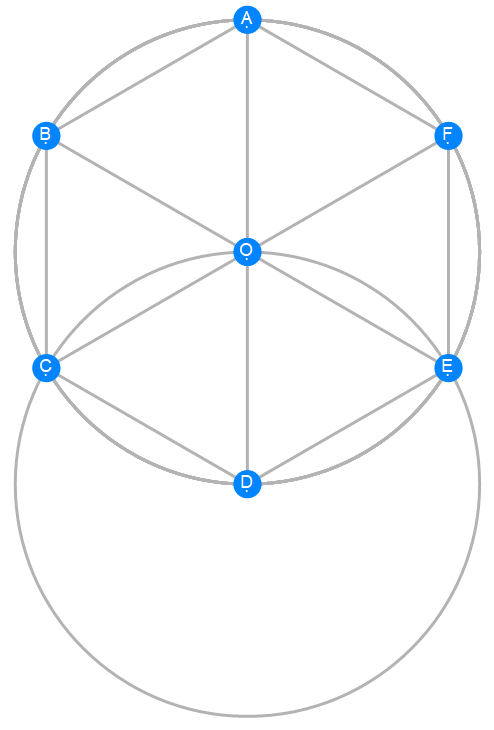
Euclid Book 4 Proposition 15
-
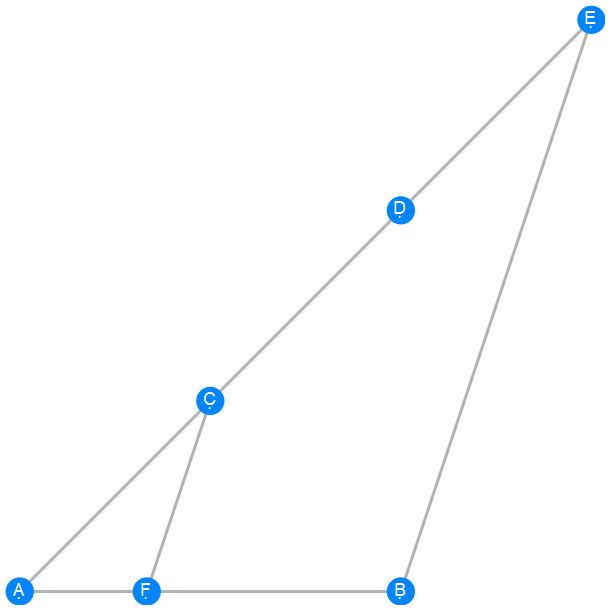
Euclid Book 6 Proposition 9
-
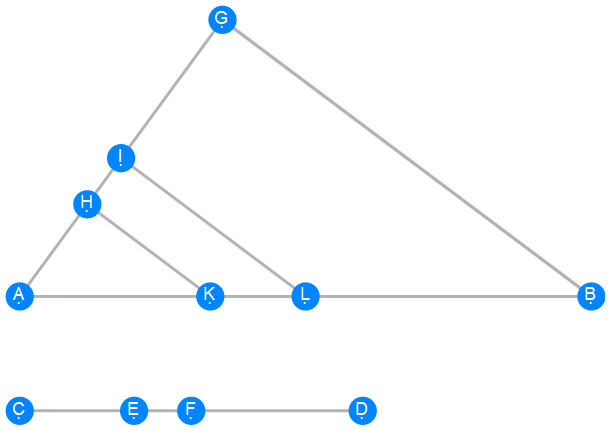
Euclid Book 6 Proposition 10
-
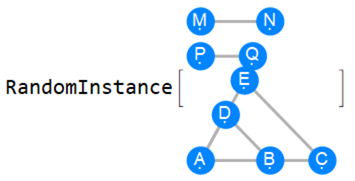
Euclid Book 6 Proposition 11
-
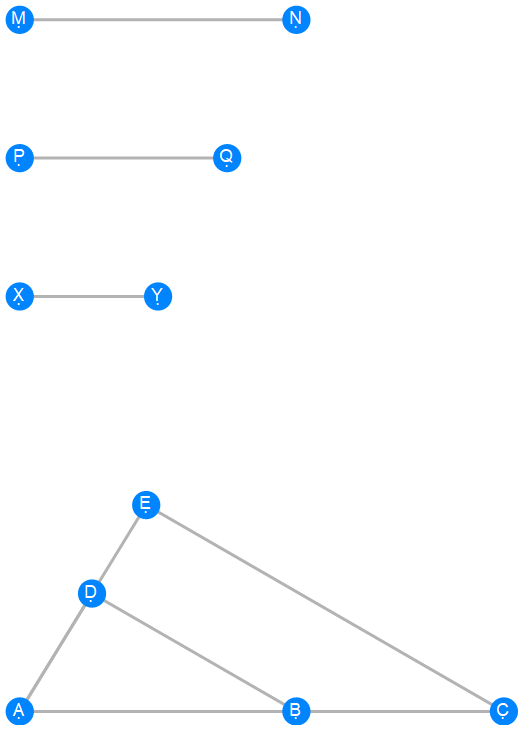
Euclid Book 6 Proposition 12
-
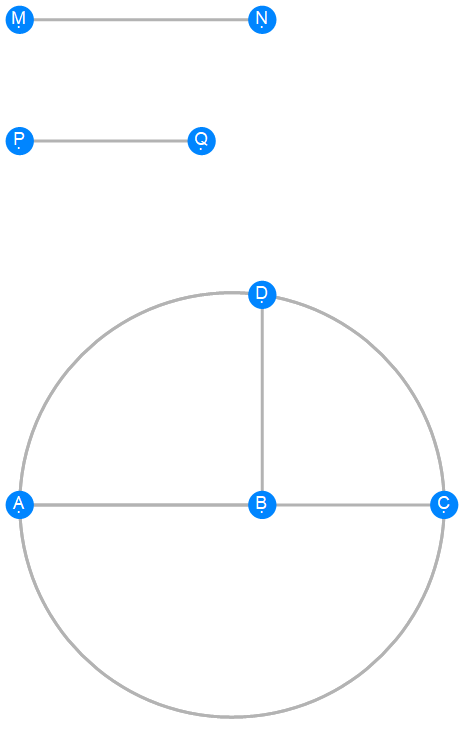
Euclid Book 6 Proposition 13
-
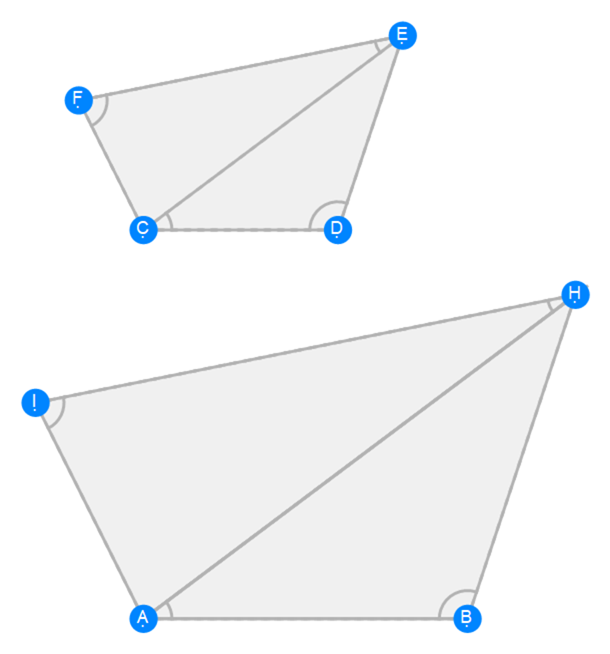
Euclid Book 6 Proposition 18
-
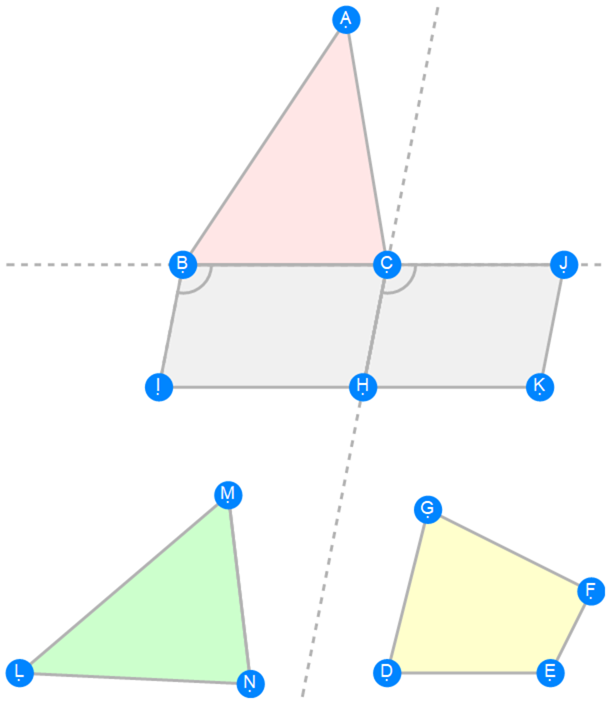
Euclid Book 6 Proposition 25
-
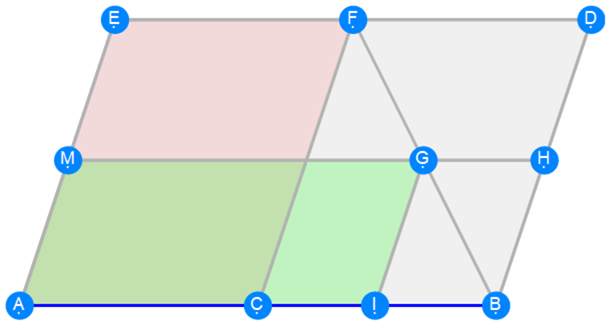
Euclid Book 6 Proposition 27
-
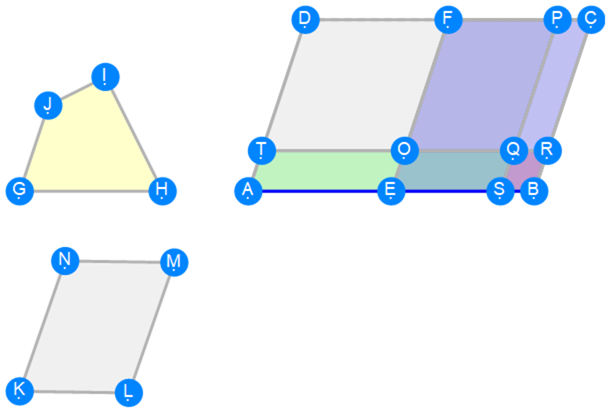
Euclid Book 6 Proposition 28
-
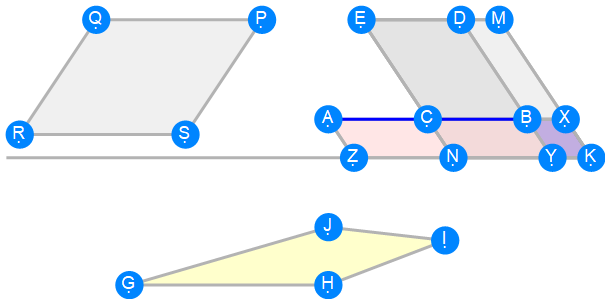
Euclid Book 6 Proposition 29
-
Euclid Book 6 Proposition 30