Computable Euclid

Euclid Book 6

Book 6 brings proportions of Book 5 to the geometry of books 1-4 to construct and recognize similar figures in a variety of ways. Proposition 3 is the angle bisector theorem. Proposition 5, sometimes known as AAA, proves that similar triangles (those with sides in proportion) have the same angles.

• Definitions

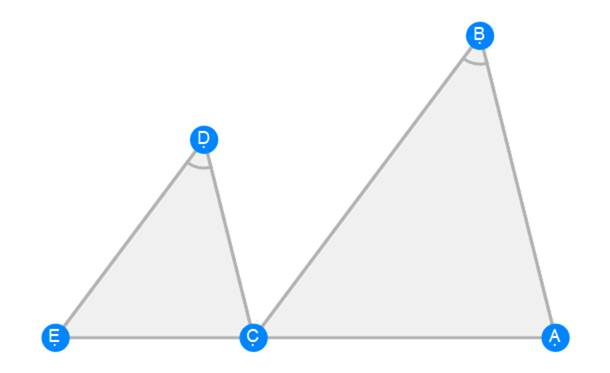
• Euclid Book 6 Proposition 1a

  

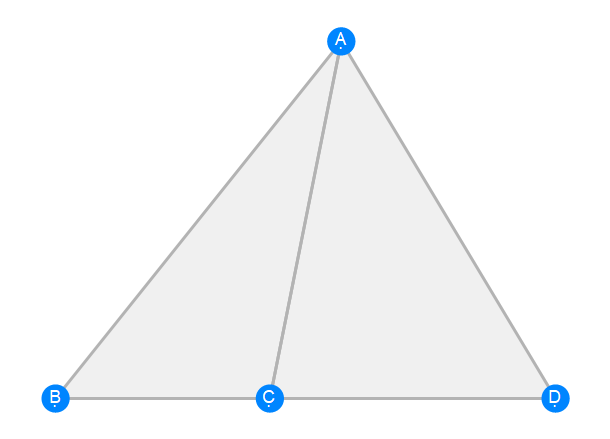
• Euclid Book 6 Proposition 1b

  

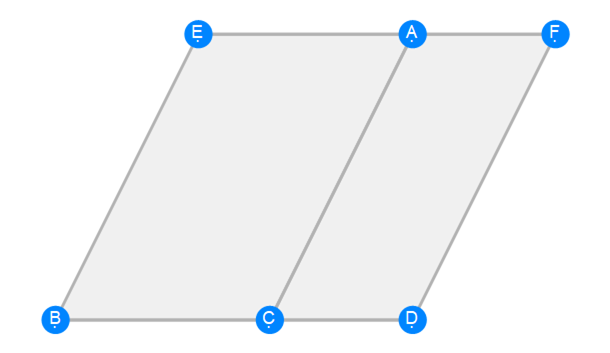
• Euclid Book 6 Proposition 2a

  

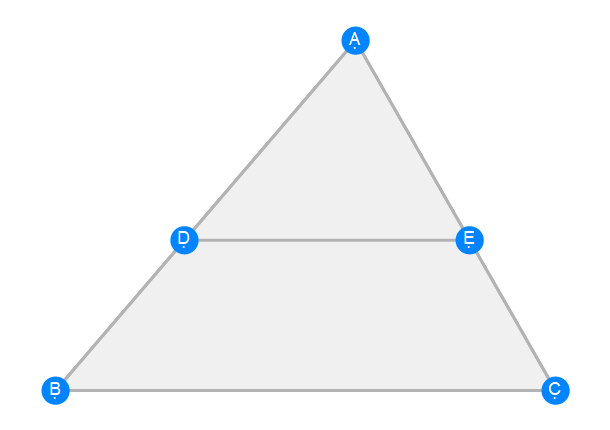
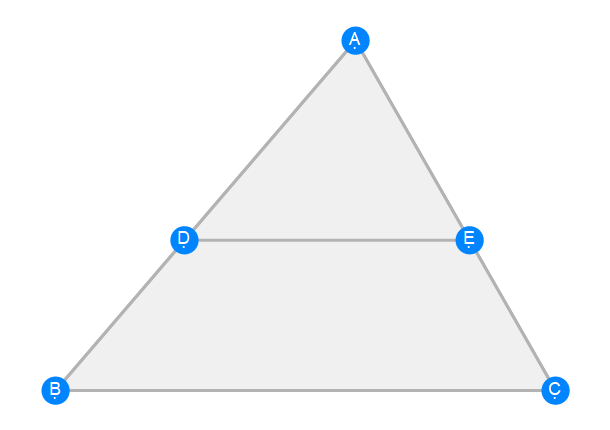
• Euclid Book 6 Proposition 2b

  

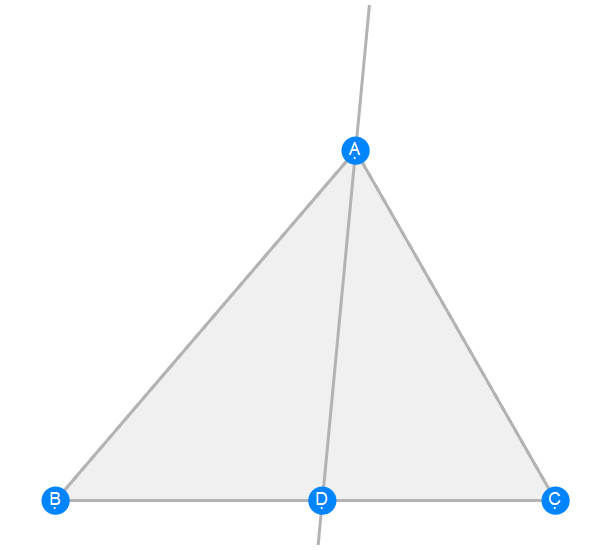
• Euclid Book 6 Proposition 3a

  

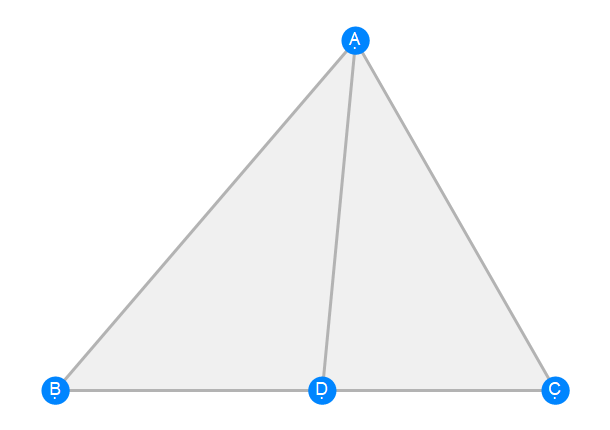
• Euclid Book 6 Proposition 3b

  

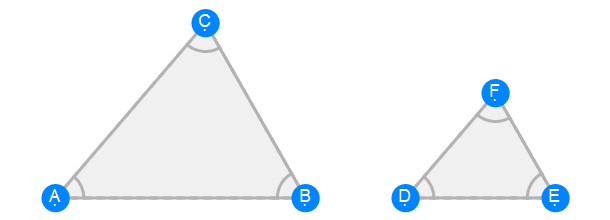
• Euclid Book 6 Proposition 4

  

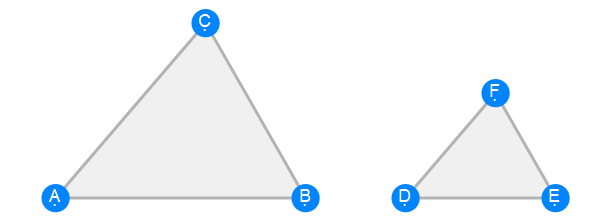
• Euclid Book 6 Proposition 5

  

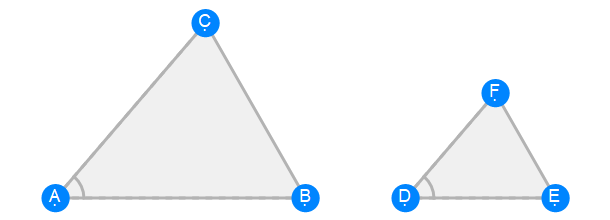
• Euclid Book 6 Proposition 6

  

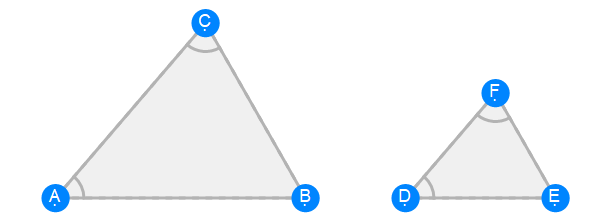
• Euclid Book 6 Proposition 7a

  

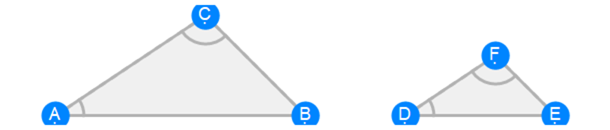
• Euclid Book 6 Proposition 7b

  

• Euclid Book 6 Proposition 8

  

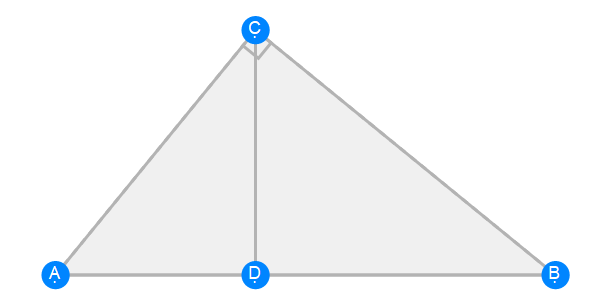
• Euclid Book 6 Proposition 9

  

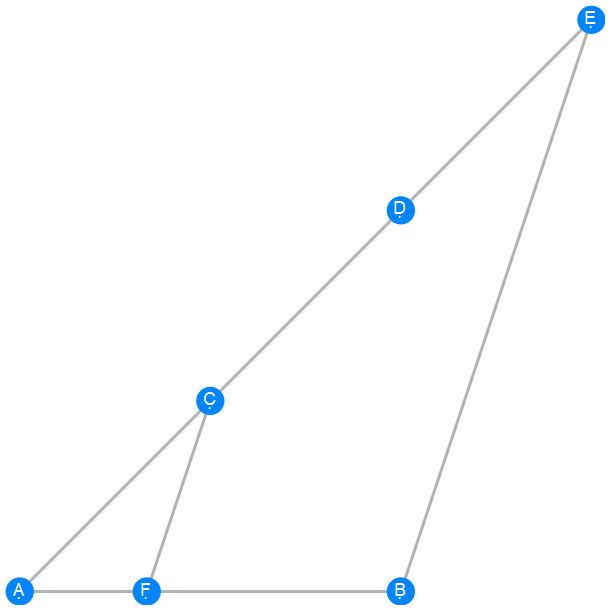
• Euclid Book 6 Proposition 10

  

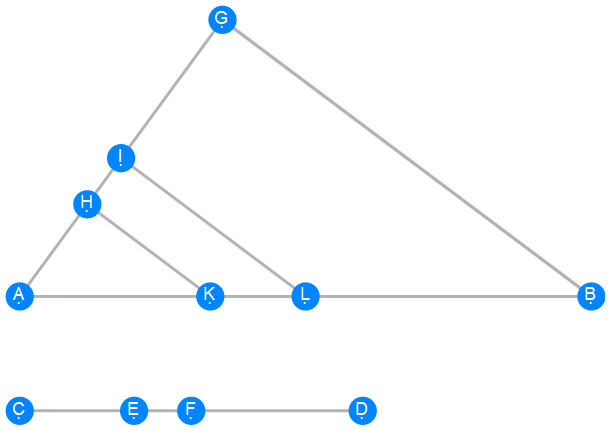
• Euclid Book 6 Proposition 11

  

• Euclid Book 6 Proposition 12

  

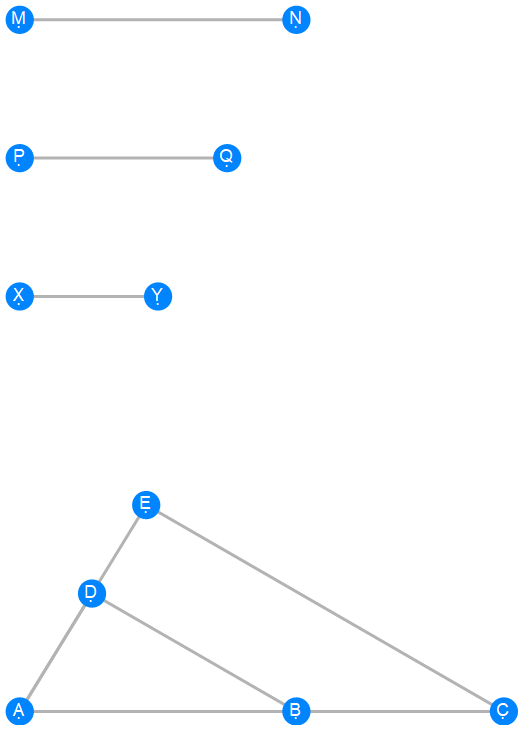
• Euclid Book 6 Proposition 13

  

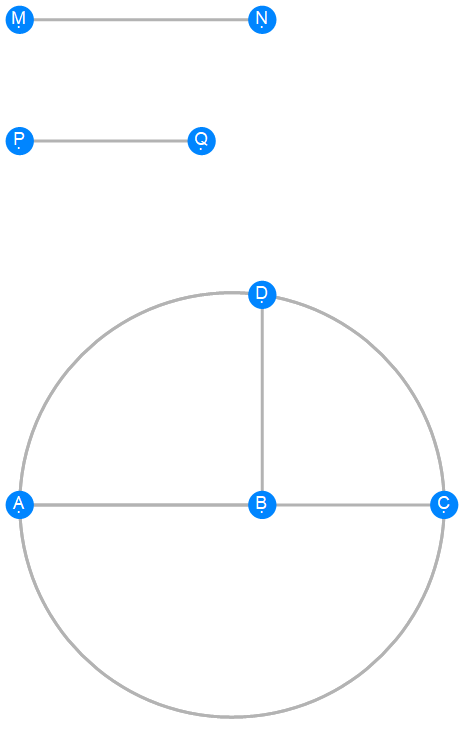
• Euclid Book 6 Proposition 14a

  

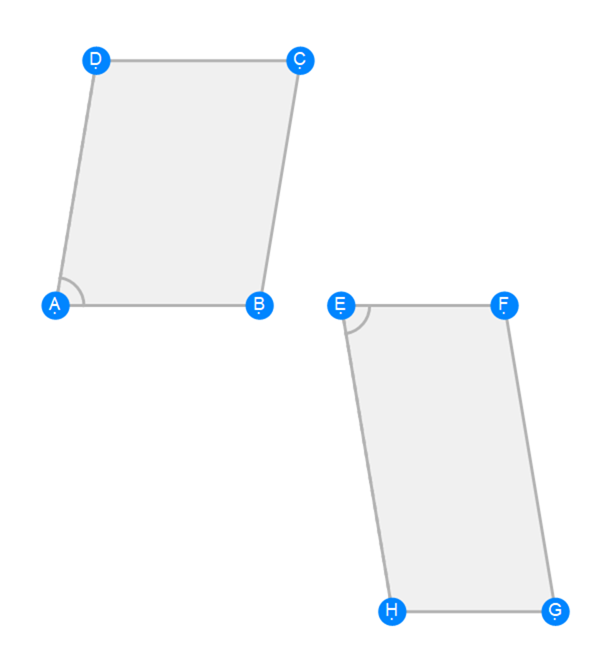
• Euclid Book 6 Proposition 14b

  

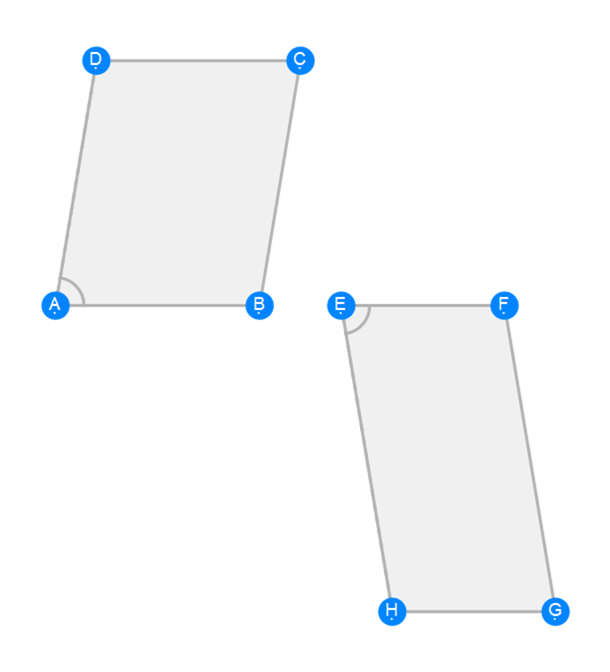
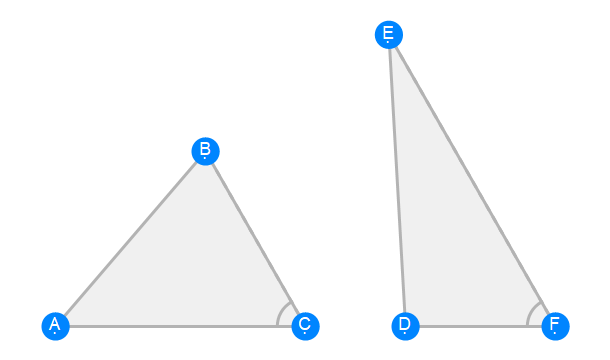
• Euclid Book 6 Proposition 15a

  

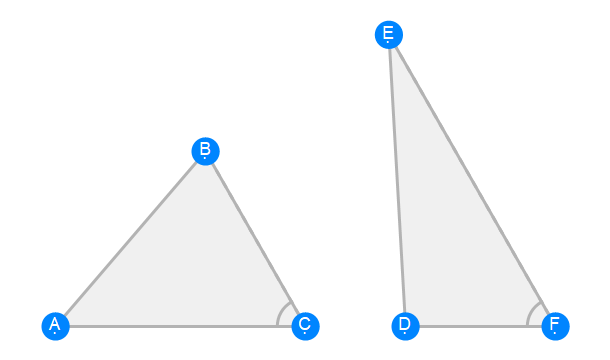
• Euclid Book 6 Proposition 15b

  

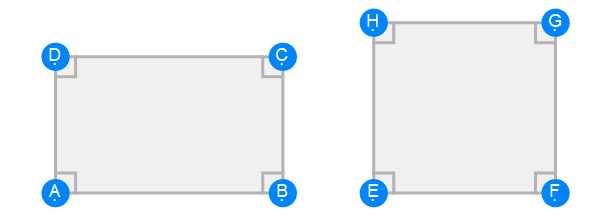
• Euclid Book 6 Proposition 16a

  

• Euclid Book 6 Proposition 16b

  

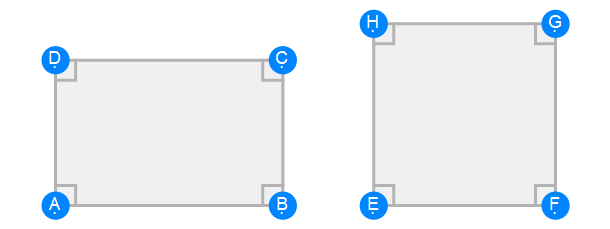
• Euclid Book 6 Proposition 17a

  

• Euclid Book 6 Proposition 17b

  

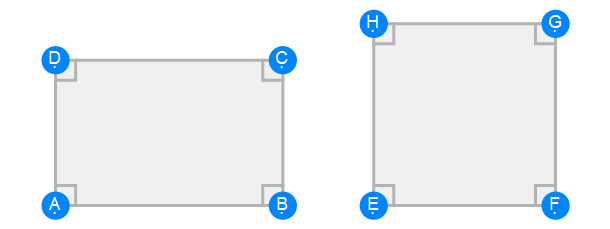
• Euclid Book 6 Proposition 18

  

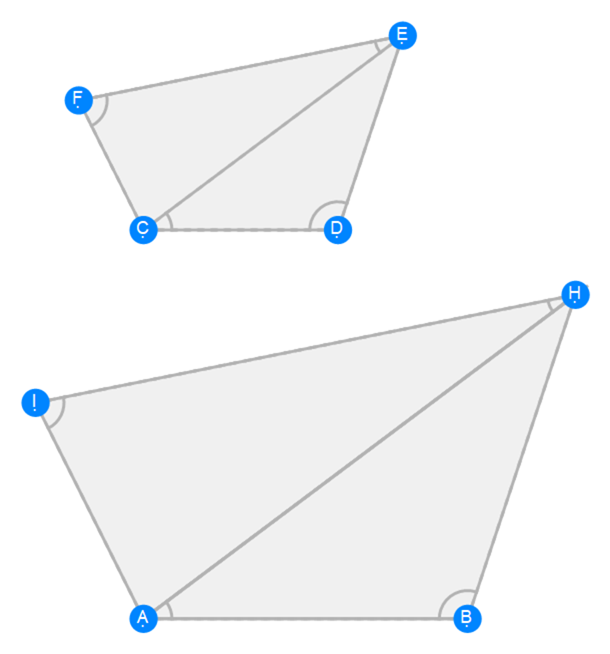
• Euclid Book 6 Proposition 19

  

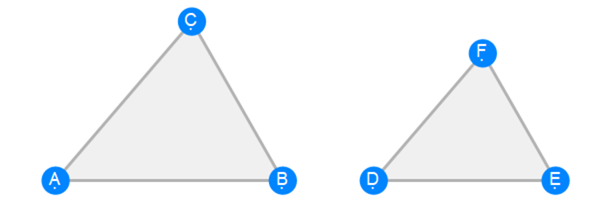
• Euclid Book 6 Proposition 20

  

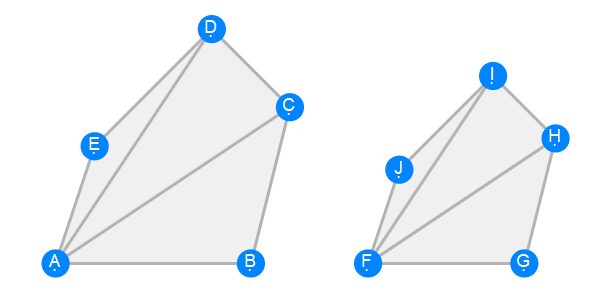
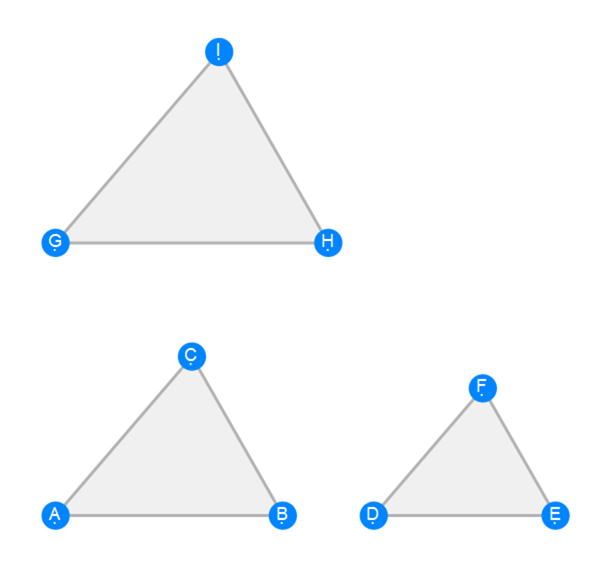
• Euclid Book 6 Proposition 21

  

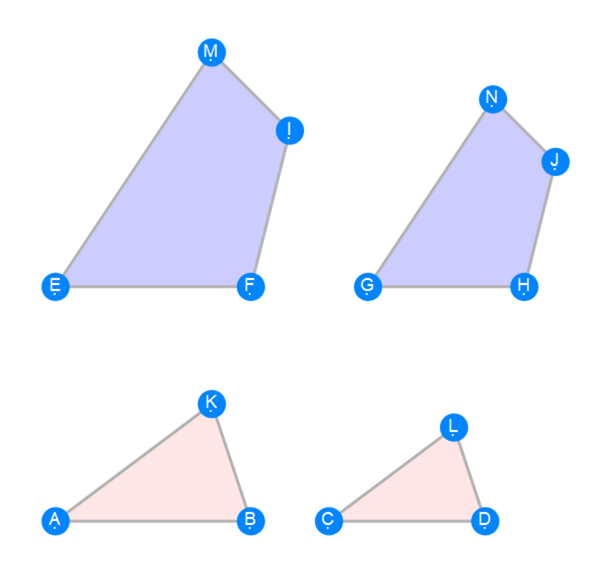
• Euclid Book 6 Proposition 22a

  

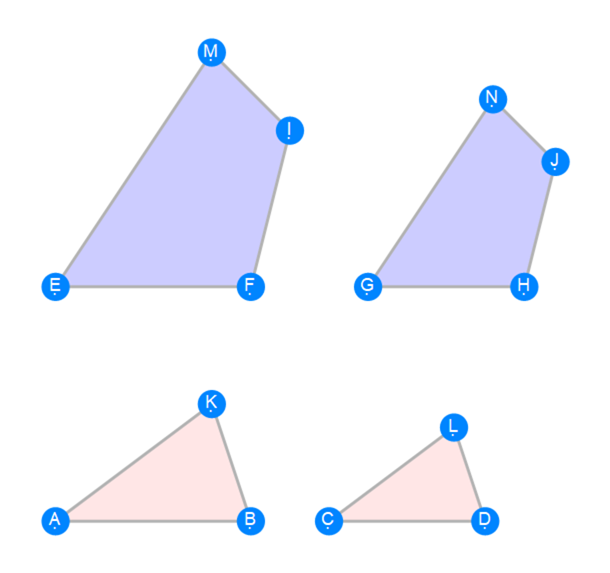
• Euclid Book 6 Proposition 22b

  

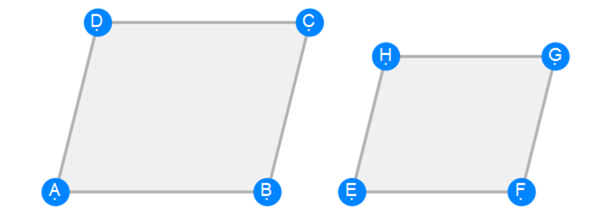
• Euclid Book 6 Proposition 23

  

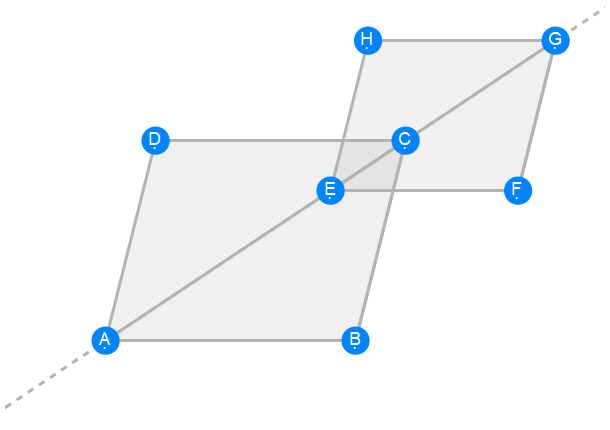
• Euclid Book 6 Proposition 24

  

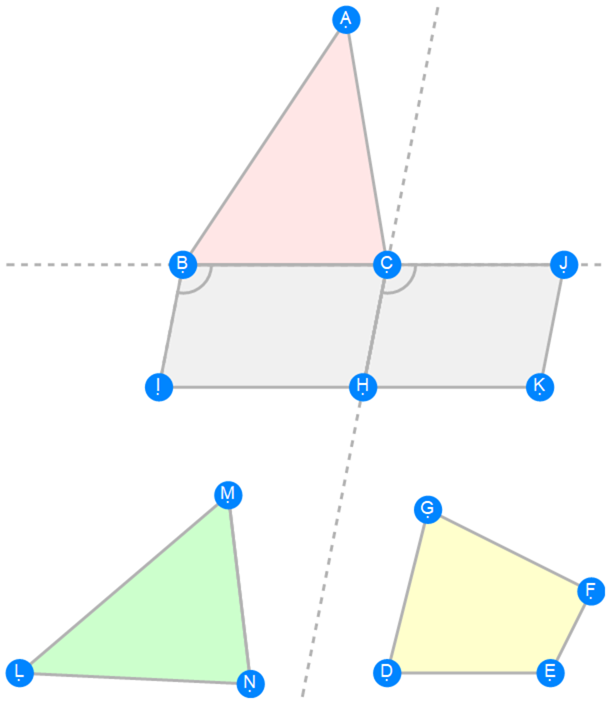
• Euclid Book 6 Proposition 25

  

• Euclid Book 6 Proposition 26

  

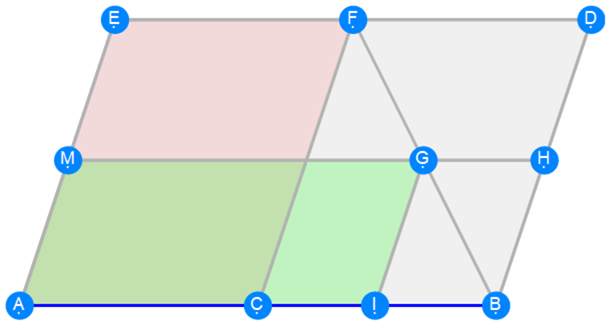
• Euclid Book 6 Proposition 27

  

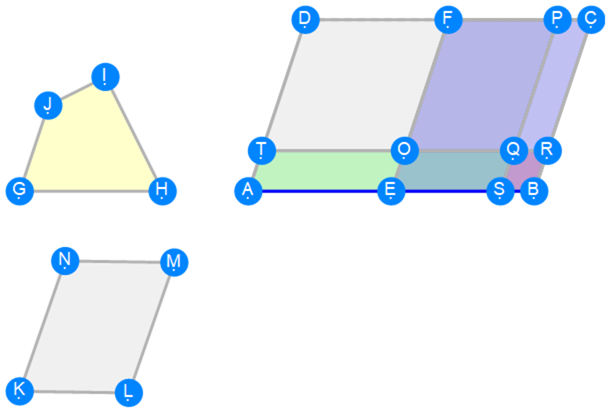
• Euclid Book 6 Proposition 28

  

• Euclid Book 6 Proposition 29

  

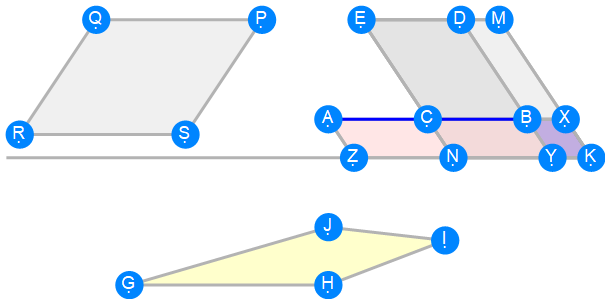
• Euclid Book 6 Proposition 30

  

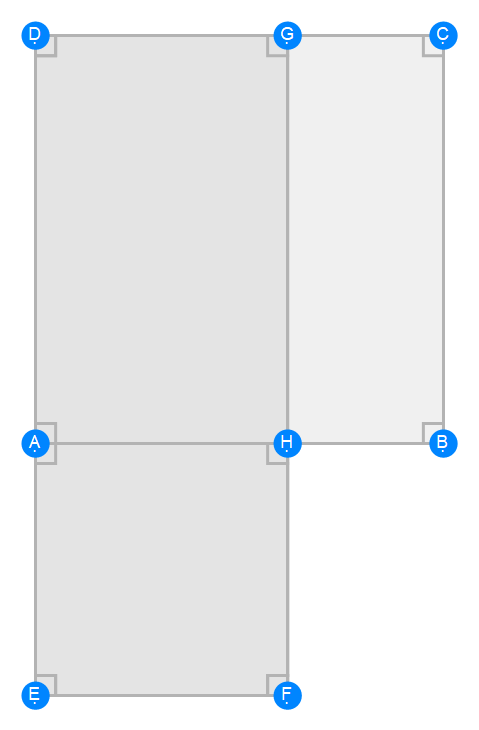
• Euclid Book 6 Proposition 31

  

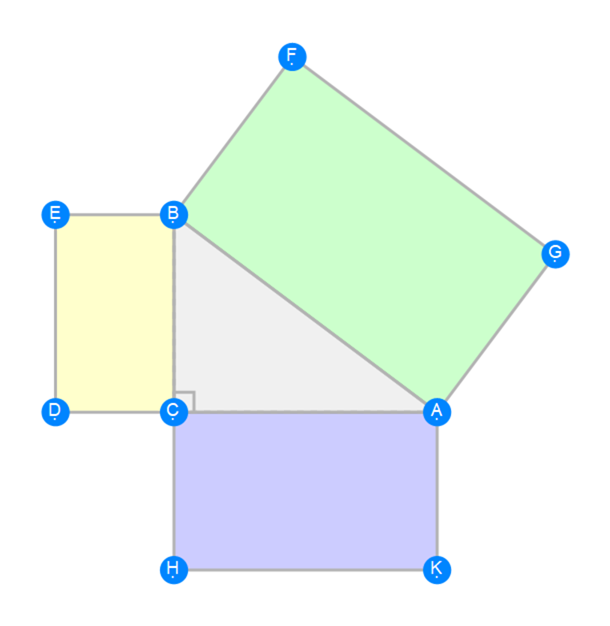
• Euclid Book 6 Proposition 32