Get data from WDR for South Korea
In[]:=
sk=ResourceData["Epidemic Data for Novel Coronavirus COVID-19","WorldCountries"]SelectFirst#Country==&,{-3;;}//Normal//First;
Calculate [active] infected population
In[]:=
infected=Query[#ConfirmedCases-(#RecoveredCases+#Deaths)&]@sk;
In[]:=
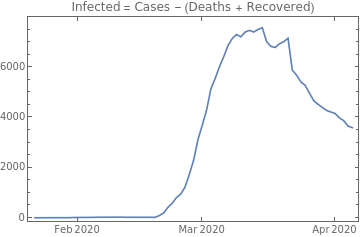
DateListPlot[{infected},PlotLabel"Infected = Cases - (Deaths + Recovered)"]
Out[]=
{day,value} for the active infected population
In[]:=
data=MapIndexed[{#2[[1]],#1}&,infected["Values"]];
Find a numerical solution based on SIR model
In[]:=
solI=ℐ/.ParametricNDSolve'[t]-β[t],ℐ'[t]β[t]-γℐ[t],ℛ'[t]γℐ[t],[0],ℐ[0]1,ℛ[0]0,{,ℐ},{t,0,90},{,β,γ}
ℐ[t]
ℐ[t]
Out[]=
ParametricFunction
Find fitting parameters manually
In[]:=
Manipulate[Plot[solI[nn,beta,gamma][t],{t,0,90},EpilogPoint@data],{{nn,17000,"Population"},10000,100000,Appearance"Labeled"},{{beta,.27,"β"},0,1,Appearance"Labeled"},{{gamma,.06,"γ"},0,.1,Appearance"Labeled"},SaveDefinitionsTrue]
Out[]=
Find fitting parameters automatically
In[]:=
fit=FindFit[data,solI[,β,γ][t],{{,10000},{β,.3},{γ,.02}},t]//Quiet
Out[]=
{16362.6,β0.27327,γ0.0570957}
In[]:=
Plot[solI[,β,γ][t]/.fit,{t,0,90},Epilog{Point@data}]
Out[]=
The so-called basic reproduction number (also called basic reproduction ratio)
In[]:=
R0=β/γ/.fit
Out[]=
4.78618