Birthday Paradox Probability Estimates
Birthday Paradox Probability Estimates
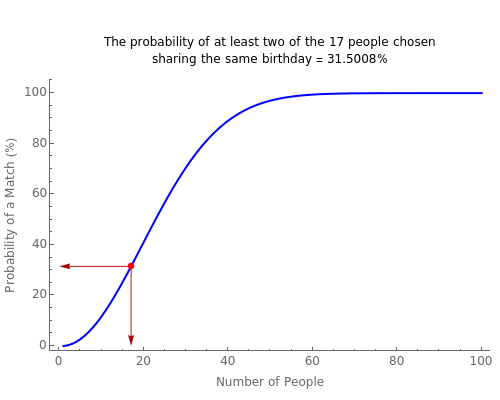
This Demonstration of the birthday problem shows the probability that at least two individuals share the same birthday assuming that there are 365 equally likely possible birthdays.
You may be surprised to find that if you randomly select 23 people there is just over a 50% probability that at least two of the individuals will share the same birthday. Move the slider to add more people and see how the probability increases. At around 57 people you should find the probability of a match reaches approximately 99%.
Details
Details
The formula for the probability of some people out of to share the same birthday is:
n
1-(365-n)!=1-n!
365!
n
365
365 |
n |
n
365
365 |
n |
References
References
[1] E. H. McKinney, "Generalized Birthday Problem," The American Mathematical Monthly, 73(4), 1966 pp. 385–387.
External Links
External Links
Permanent Citation
Permanent Citation
Scott R. Colwell
"Birthday Paradox Probability Estimates"
http://demonstrations.wolfram.com/BirthdayParadoxProbabilityEstimates/
Wolfram Demonstrations Project
Published: August 5, 2011