Bézier Curve by de Casteljau's Algorithm

r

1

2

3

t

As

r

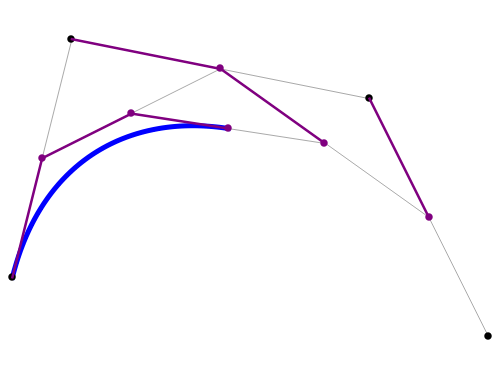
changes from 1 to 3 a sequence of linear interpolations shows how to construct a point on the cubic Bézier curve when there are four control points. The parameter

t

controls the proportion of the distance along an interpolating line. As

t

varies between 0 and 1 the entire curve is generated.

Details

For

n+1

control points,

p

0

,

p

1

,...,

p

n

, the Bézier curve can be constructed by the recurrence relation

r

B

i

(t)=(1-t)

r-1

B

i

(t)+t

r-1

B

i+1

(t)

where

1

B

i

=(1-t)

p

i

+t

p

i+1

is the linear interpolation between control points

p

i

and

p

i+1

. The recursion level

r

goes from 1 to

n

and

i

runs from 0 to

n-r

.

External Links

Bézier Curve (Wolfram MathWorld)

Permanent Citation

Bruce Atwood

"Bézier Curve by de Casteljau's Algorithm"
http://demonstrations.wolfram.com/BezierCurveByDeCasteljausAlgorithm/
Wolfram Demonstrations Project
Published: September 28, 2007