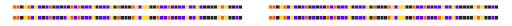Nature’s Compass: A visual exploration of hierarchy in biology and beyond
Nature’s Compass: A visual exploration of hierarchy in biology and beyond
Anyone who gets into science is, by nature, a bit of a curmudgeon. I was always that kid holding up class to argue with the teacher.
Luckily there are some benefits to being stubborn, which is that you occasionally figure something out that most people don’t understand, just by virtue of being unsatisfied with the current explanations.
It’s popular right now for intellectuals to use status, hierarchy, pecking order, whatever you want to call it, as an explanation for various human behavioral phenomenon. Jordan Peterson emphasizes its ubiquity in his book “12 Rules For Life”. He points out that people at the top of the hierarchy are healthier in various ways, suggesting to the reader to “aim up” and attempt to climb the ranks of society.
While compelling, this perspective left a bad taste in my mouth; I couldn’t shake the depressing feeling that the pie of well-being was fixed, and the only thing to do was grab as much for yourself as possible.
After some reflection and experimentation though, I’ve realized that in many cases hierarchy is not just some Malthusian scramble for resources, but it is a powerful steering mechanism for evolving systems, including human society.
Hierarchy in our culture is often debated in the realm of morality, but I think it actually has clear computational foundations. Building on Stephen Wolfram’s new model for biology: so-called adaptive cellular automaton, we can extract the computational essence of hierarchy. And in examining these foundations, we will learn that we ought to embrace hierarchy and not avoid it.
Our creatures
Our creatures
My core idea here, is that hierarchy is prominent at many levels in biology, from genomes to societies, and in cases where there is dependence between organisms, it functions as the compass for the group’s survival.
Using the Wolfram model, we can poke and prod computational critters to get to the heart of biological processes.
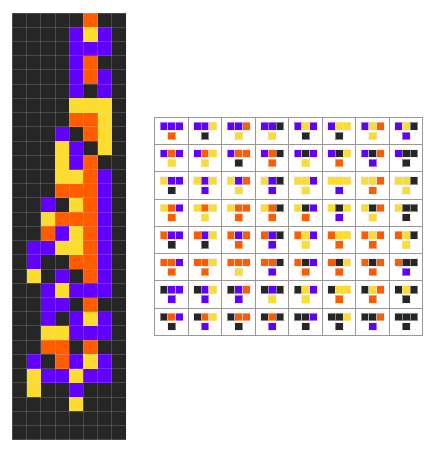
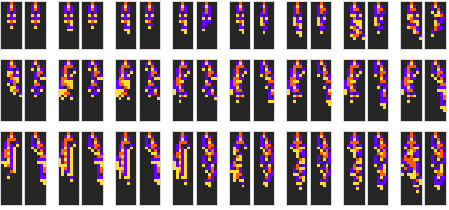
In Wolfram’s model, we have a set of updating rules that act on colored cells to produce a simple program that is meant to be an idealized organism:
Out[]=
We then just align each bottom box in the grid of rules horizontally to get a “gene”:
Out[]=
To evolve the organism, we recursively mutate the gene keeping only the mutations that result in longer or equal finite length, or in biological terms, higher fitness. One difference here in our model, is we’re only allowing length increases of at most one, this is to slow down evolution and allow us to better compare different approaches. Here we show the breakthrough automata after two-hundred and fifty steps of evolution:
Out[]=
And here is the corresponding evolution of the rules:
Out[]=
Hierarchical Evolution
Hierarchical Evolution
To explore the concept of hierarchy, we will use this exact setup, but instead of one automaton evolving, we have two automaton simultaneously evolving:
Out[]=
In an evolution we mutate both genes individually and simultaneously, randomly flipping a rule in each gene:
Out[]=
We repeat this process as in the normal evolution, with the difference being that if one of the automaton lives longer than the other, then that one replaces the other.
The most obvious example of this in biology is in populations evolving with sexual selection.
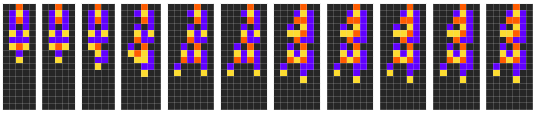
In sexually reproducing organisms, an individual from one sex is incentivized to find metrics of fitness in the other, because their offspring will share genes in the future. In the language of sociology, these metrics are symbols of status, and in this setup, the high-status females will only mate with the high-status males. This means that high-status, and therefore high-fitness genes have a higher probability of surviving. In our experiment, for understanding’s sake, we take this to the extreme and have the higher-fitness individual occupy the entire population of the next generation. Here is an example of our hierarchical evolution:
The most obvious example of this in biology is in populations evolving with sexual selection.
In sexually reproducing organisms, an individual from one sex is incentivized to find metrics of fitness in the other, because their offspring will share genes in the future. In the language of sociology, these metrics are symbols of status, and in this setup, the high-status females will only mate with the high-status males. This means that high-status, and therefore high-fitness genes have a higher probability of surviving. In our experiment, for understanding’s sake, we take this to the extreme and have the higher-fitness individual occupy the entire population of the next generation. Here is an example of our hierarchical evolution:
Out[]=
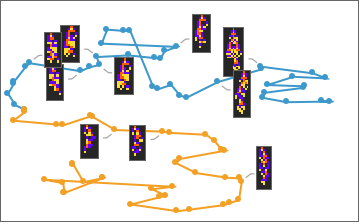
The patterns with green frames are ones where a breakthrough mutation was made, and that “male” was chosen. Notice that after a discovery is made, that pattern then replaces the other pattern resulting in two identical automaton on the next step. Plotting this evolution in “genome space” we get the following:
Out[]=
Here we are using a machine learning algorithm to reduce the “genome” into two dimensions. Notice how the organisms deviate from each other, and then, when a discovery is made, the less fit organism is “pulled” to the more fit one.
So how does hierarchical evolution compare to “normal” evolution?
We now run an evolution where each individual in the population evolves independently from each another. We can imagine this as the females mating equally with both males:
Out[]=
Basically, in doing individual evolutions we’re not allowing the current most fit organisms to dominate the gene pool. We can clearly see there is more variation between the organisms, but we can also see that they didn’t make it as far as the hierarchical group, and this is no accident.
Plotting the regular evolution in genome space we get:
Out[]=
So we can see that this group is searching the fitness landscape independently from one another, we do not see the “attraction” we observed in the hierarchical evolution.
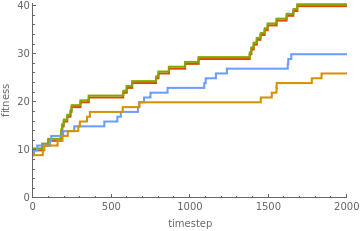
How much further did the hierarchical search get? Looking now only at the fitness (length), of each automaton, we get:
Out[]=
Visibly, the hierarchical pair is climbing significantly higher. Doing twenty iterations we get:
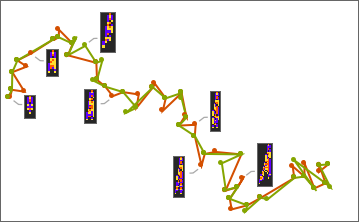
Clearly, the hierarchical approach is leading to faster evolution. Combining the genome plots with the fitness plots for the hierarchical population, we get:
Here the 2D plane corresponds to genome space, and the height at each point corresponds to the fitness of the organism. We can see it’s almost as if the two automaton are climbers belaying each other up the mountain.
We can think about each jump in height as when an organism discovers a way to become more fit. The high-status female (or male) observers would then recognize this, and mate with them. Because of that, the population is then “pulled” towards that individual. We only have two organisms here for visualization purposes, but in real life this is happening with many different organisms simultaneously.
In contrast, the non-hierarchical population, here in blue and orange, wander independently:
Said in a different way, hierarchical populations only search near the current best ideas. The more clustered the good ideas are, the better this will work. The universality of sexual selection and hierarchy in animal societies is a strong indication that good ideas tend to cluster in real-world evolutionary landscapes.
Zooming out, traditional explanations for the evolutionary benefit of sex emphasize that combining ideas allows evolution to move faster. While this no doubt makes sense, what we’re observing here offers an alternative explanation, which is that sharing genes gives the population the chance to self-evaluate, and therefore more effectively direct the evolutionary search.
To be clear, we are still assuming that each member of the group is acting selfishly.
But critically, this also benefits the group in the long-run. At a single generation, the pie is indeed fixed, but looked at over time, there is no telling what a species can achieve. The best thing about biology is that it is Turing-complete, it is infinitely creative and there are endless discoveries to be made. We’ll see later why there’s no reason to believe this doesn’t translate to human societies.
But critically, this also benefits the group in the long-run. At a single generation, the pie is indeed fixed, but looked at over time, there is no telling what a species can achieve. The best thing about biology is that it is Turing-complete, it is infinitely creative and there are endless discoveries to be made. We’ll see later why there’s no reason to believe this doesn’t translate to human societies.
We’ve been talking about these automaton as organisms, but they could also correspond to individual genes within an organism. For instance, it is known that when the human immune system is under attack from a virus, it mutates it’s own genome until it finds the right protein shape for catching that virus. It then removes all the other proteins and mass produces the winner. In our model here, the genes for the protein would be our automata and the selector would be the immune system.
Similarly, we can imagine genetic repair and replacement as an evaluation and selection of higher fitness genes. This is not far-fetched, given that it is believed that horizontal gene transfer in bacteria was originally evolved as a mechanism for gene repair. Meaning, the bacteria have some way of identifying there own damaged genes and replacing them with genes from other organisms. In this case, the automaton in question would be the replacement and damaged genes. The selectors would be biological machinery involved in the repair.
More generally, there is a movement happening in biology right now called, “The Fourth Synthesis”. Among other things, it is emphasizing the agency of low-level components in biology, which was originally minimized by the Neo-Darwinists, including the buffoon Richard Dawkins. For instance, there are now studies showing that the gene activation pattern of the parent can be passed on to the child, so-called epigenetic inheritance. What this means is that in principal, an organism could choose between two genes, within it’s lifetime, and pass that choice on to it’s child, which is very similar to our hierarchical evolution above.
Put simply, hierarchical evolution can happen at a much lower-level and across a shorter time frame than was previously thought. Our model predicts that systems are highly incentivized to lean into hierarchical evolution, which seems to agree with the findings of the fourth synthesis.
The symbolic layer of evolution
The symbolic layer of evolution
Our model of hierarchy thus far has abstracted away the notion of death and simply used the metric of fitness. But, I find it helpful to look at a model that’s even more bare bones, that simply starts by defining life and death. In doing this, we’ll see that hierarchy is really a symbolic layer on top of life and death. Evolution is then latching on to features that are associated with survival and finding mechanisms that allow organisms with those features to dominate the gene pool.
In our simpler model, we will have a branching population of organisms. The x-axis represents time and the y-axis corresponds to the “phenotype” of the organism. After a period of time, the organism “reproduces”, splitting into two separate organisms. The branching radius corresponds to variation between generations. We add some additional variation to that radius just so we can better visualize the population and avoid overlaps:
With this setup, we can already capture some essential features of evolution. For instance, we can imagine a more conservative population with a lower branching radius, or a lower “mutation rate”. Here the children are more like their parents:
Or we could decrease the lifetime, effectively increasing the reproduction rate and leading to a “faster-adapting” organism:
Notice how the organisms closer to the center are warmer colors, we will use this to distinguish phenotypes.
Now we can embed our population onto a “fitness ridge”. Here, if an organism lands outside of the ridge, they die:
Notice how the environment carves the phenotype of the population just like in evolution. The “purple organisms” we’re removed from the population by the change in the environment, leaving only the “orange organisms”. When the road widens again in a time of “energy-abundance” the purple organisms make a reappearance.
There is an important subtlety here which is that there are “potholes” that we didn’t show in the previous image:
Anytime an organism runs into one of the potholes during their lifetime (the horizontal line) they die. This is necessary to limit the population growth and add some randomness to the environment just like in the real world.
So, the above population is successfully navigating the fitness landscape. But we can look at situations where normal evolution struggles. Increasing the height of our ridge, or in other words, increasing the variation in the environment, we get:
So with a slightly larger variation in the ridge, the above population struggles. However, organisms with a higher branching radii, or “mutation rate”, can deal with this no problem:
This can be taken too far if the variation exceeds the width of fitness-space:
Generalizing here, the rate of variation in organisms will match the rate of variation in the environment, up to the width of the fitness space.
I suspect that this is the reason for the low mutation rate observed in biology. Given the presence of irreducibility, the effects of such a low-level change like a mutation, can be enormous. We can think about a branch here as a point mutation, with the potential for a huge jump away from your current phenotype. This is an extreme risk especially from the perspective of the individual organism. In contrast, starting from larger building blocks and combining them through sexual reproduction results in milder and more directed variation.
But at some point, if we increase the rate of change as well as the narrowness of the ridge enough, then there is no single level of variation that can navigate the landscape:
In evolutionary terms we can think of this as the variation and precision demanded from the environment. The environment up until step twenty is mellow and tolerant of many different phenotypes, like the period during the Cambrian explosion or the Dinosaur age. But a change causes a squeeze in phenotypic space, maybe the population gets exposed to a novel parasite, or there’s a sudden change in climate.
This squeeze means that most phenotypes will not work anymore, therefore only the high variance organisms can deal with the bank in the road. But, If you vary enough to be able to adapt to the change, then when you enter into the narrow section, you will be unable to be precise enough to “stay the course”.
Now one approach to deal with this is to find a mechanism for controlling your variation based on the stress-level of your environment. And as we highlighted above with the human immune system, this does in fact happen. Random mutation is not fully random in the sense that the rate is controlled by the organism in many cases.
And I’m sure we could get this to work in our model, but in going with our theme of hierarchy, I’m going to show a different approach. Namely, we will allow the population to determine the organism that is closest to the center of the road, the organism that has the most “orangeness”. Then, they will direct their offspring closer towards that “high-status individual”.
Here is what our procedure looks like up close:
Notice how the branches are now shooting towards the individual that is closest to the center of the plot. When they get to the middle they stabilize (with some randomness). Running our hierarchical evolution in that same harsh environment we see that it passes with flying colors:
In always trying to get to the center of the road, this population is able to pull more of its organisms above the bank, which gives it the momentum to navigate the dangerous narrow ridge. The reason this works, is there is some reducibility in the environment. Namely, organisms that are closer to the center of the road, or in our case more orange, always have a higher probability of survival. Organisms that are able to recognize and act on this reducibility, are the ones that survive. Over time, a symbolic layer on top of life and death is established. And it is the predictive capacity of this layer that enables the population to thrive.
The Largest Organisms To Ever Exist
The Largest Organisms To Ever Exist
Human civilization is the largest, most powerful organism to ever exist. It’s strength, specialization, is also its weakness: If one thing within the civilization goes wrong, the whole thing can collapse.
Over time, the surviving civilizations developed cultural tumor detectors in the form of religion, law and economy. The more you harvested, the more you got paid. If you were stealing, you were banished. If you were wise, you were protected. If you were spreading disease through promiscuity, you were outlawed. If you died in battle, your family was honored. If you weren’t taking your anger out on animals every Sunday, you were excommunicated. If you didn’t believe that there was a giant man in the sky that controlled every aspect of your life, from who will be the next king to when your dog will take his next shit... I think you get the point.
These immuno-cultural mechanisms were adapted and improved over time. Interestingly, the “Sunday animal anger” and the “giant man in the sky” ideas were both big hits, which speaks to the fact that it’s not always clear how these processes work.
The staying power of the status symbols like wealth, sense of humor, cleanliness, certain religious ideals like sexual conservatism, respect, and erudition are tremendous indications of their validity. And, given the fact that I’d prefer if our society didn’t collapse, I’ve become a status maximalist. I try to be the most rich, well-liked, well-read, noble, law-abiding, god-fearing (in a loose sense) man I can be.
I speak dramatically here to avoid boring myself and the reader, but I think that status maximalism, in most cases, is the way to go.
A strong sense of gratitude, humility and kindness, stemming in the West from Christianity, is a good indicator of the health of a system, but surprisingly seems to be an indicator of individual success as well. Nobody likes spitefulness I guess. The best opportunities I’ve got seemed to come when I was the most grateful.
People often try to get rich for themselves and be kind for the sake of others. I say, get rich for others, and be kind for your own sake. And long live the hierarchy!
Thank you, reader.
Willem
Willem