MAM2046W - Second year nonlinear dynamics
MAM2046W - Second year nonlinear dynamics
Section 2.1: Limit Cycles
Section 2.1: Limit Cycles
We’re going to start with an example here.
Taking the vector field in polar coordinates:
r
2
r
θ
and converting these to Cartesian coordinates:
x
3
x
2
y
y
3
y
2
x
we can plot the vector field in the Cartesian plane along with some trajectories.
In[]:=
eqns=SimplifySolveD+,t==+)),DArcTan,t==1,{x'[t],y'[t]}[[1]];startpoints=Flatten[Permutations[{1,1,-1,-1},{2}]#&/@{2,0.1},1];({x[t],y[t]}/.NDSolve[{x'[t]==(x'[t]/.eqns),y'[t]==(y'[t]/.eqns),x[0]==#[[1]],y[0]==#[[2]]},{x,y},{t,0,10}][[1]])&/@startpoints;Show[VectorPlot[Evaluate[{x'[t],y'[t]}/.eqns/.{x[t]->x,y[t]->y}],{x,-2,2},{y,-2,2}],ParametricPlot[%,{t,0,10},PlotStyle->{{Red,Thick},{Red,Thick},{Red,Thick},{Red,Thick},{Blue,Thick},{Blue,Thick},{Blue,Thick},{Blue,Thick}}],Graphics[Arrow[{#/.t->0,#/.t->0.01}]]&/@%,ImageSize->700]
2
x[t]
2
y[t]
(+)
(1-(2
x[t]
2
y[t]
2
x[t]
2
y[t]
y[t]
x[t]
Out[]=
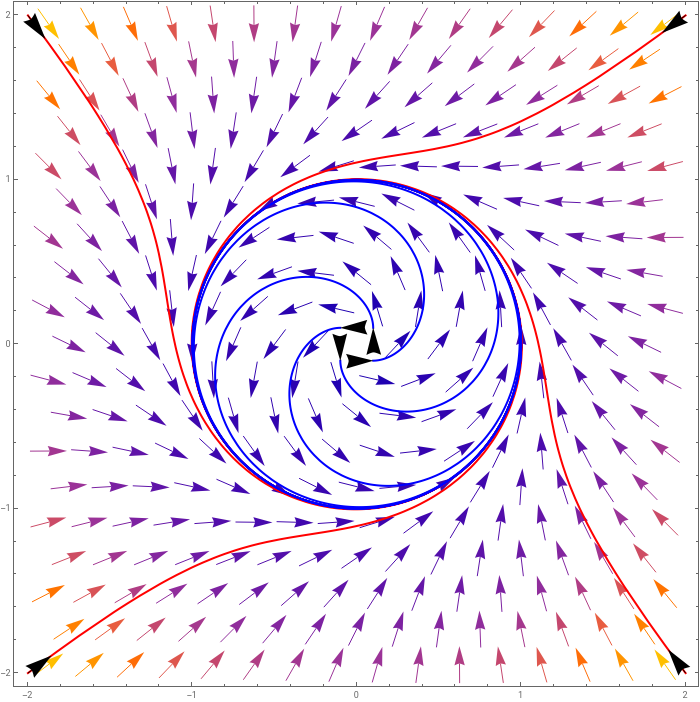
We see that this system has a center, at outside the center, then we spiral towards it. If we start inside the center then we also spiral towards it. The center seems to be attracting trajectories both outside it and inside it.
r=1.Ifwestart
This circular trajectory is called a limit cycle. The limiting behaviour of those trajectories spiraling in are the limit cycle. This is a stable limit cycle, but you can have unstable limit cycles (imagine just changing in the above), where the trajectories are repelled from it, and semi-stable limit cycles where only the inside or the outside flow towards the cycle, and the other flows away.
t->-t
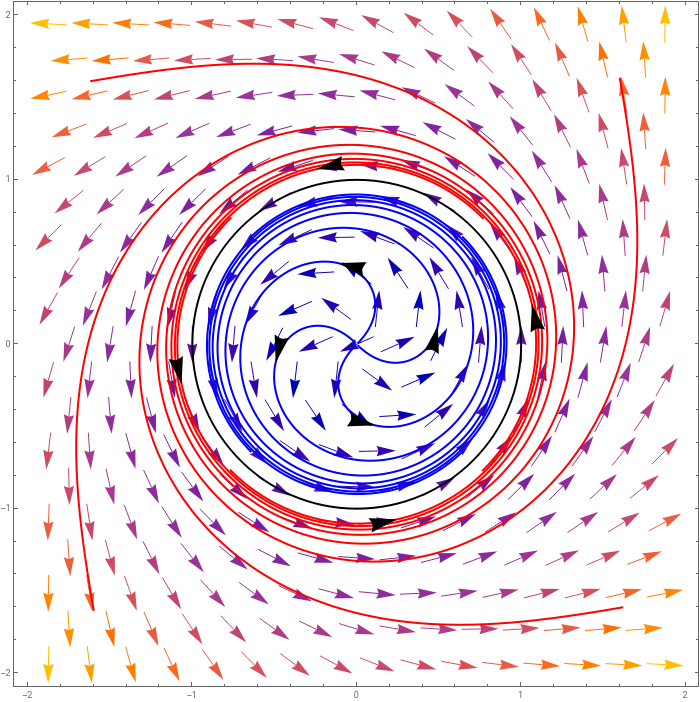
An example of a semi-stable limit cycle is given by the vector field
r
2
(1-r)
θ
In[]:=
eqns=SimplifySolveD+,t==,DArcTan,t==1,{x'[t],y'[t]}[[1]];startpoints=FlattenPermutations[{1,1,-1,-1},{2}]#&/@+0.06,0.01,1;({x[t],y[t]}/.NDSolve[{x'[t]==(x'[t]/.eqns),y'[t]==(y'[t]/.eqns),x[0]==#[[1]],y[0]==#[[2]]},{x,y},{t,0,11}][[1]])&/@startpoints;Show[VectorPlot[Evaluate[{x'[t],y'[t]}/.eqns/.{x[t]->x,y[t]->y}],{x,-2,2},{y,-2,2}],ParametricPlot[%,{t,0,11},PlotStyle->{{Red,Thick},{Red,Thick},{Red,Thick},{Red,Thick},{Blue,Thick},{Blue,Thick},{Blue,Thick},{Blue,Thick}}],Graphics[Arrow[{#/.t->1,#/.t->1.01}]]&/@%,Graphics[{Thick,Circle[{0,0},1]}],ImageSize->700]
2
x[t]
2
y[t]
2
(+)
-12
x[t]
2
y[t]
y[t]
x[t]
1
2
Out[]=
Any trajectory which starts within the limit-cycle of radius 1 is attracted to it, and any trajectory which starts outside the cycle is repelled from it.
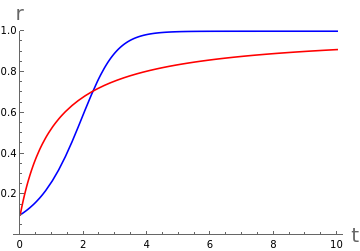
As an aside, take a look at the vector fields above (both cases) in polar coordinates and see if you can understand the phase diagram intuitively. The fact that the system is decoupled should allow you to understand what is going on quite clearly. In fact, in polar coordinates you can solve these systems exactly and see that the example of the stable fixed point goes towards the cycle much more quickly (in the long term) than in the semi-stable example. This isn’t a general principle of stable and semi-stable fixed points, but might be something that you wonder about from the trajectories above.
In[]:=
stable=r[t]/.DSolver'[t]==r[t](1-),r[0]==,r,t[[1]]semistable=r[t]/.DSolver'[t]==,r[0]==,r,t[[1]]Plot[{stable,semistable},{t,0,10},PlotRange->{0,1},PlotStyle->{Blue,Red},AxesLabel->Evaluate[Style[#,20]&/@{"t","r"}],PlotLegends{"stable example","semi-stable example"}]
2
r[t]
1
10
2
(1-r[t])
1
10
Out[]=
t
99+
2t
Out[]=
1+9t
10+9t
Out[]=
Exercise: For the above vector fields, try and plot for a number of different starting conditions.
x(t)
So how come we never saw these types of behaviour when we looked at linear systems last year? Remember we did have stable and unstable spirals, but nothing where we had solutions which spiralled towards a circle. There’s a very clear reason for this not being possible in a linear system.
Let’s say that we have some linear system given by
This then shows that in a linear system you couldn’t have a circle, and a spiral trajectory.
The Van Der Pol Oscillator
We’ve looked previously at driven and damped systems. They tend to be systems of the form
Check that the matrix of the coupled first order system of the above equation is given by:
Make sure that you can see why one is driven and one is damped.
Writing this as a coupled system we have
Think about the effect that this non-linear term might have.
Below is plotted the phase plane with some trajectories for this system:
While there is no circular solution here, there is a stable limit cycle which both trajectories starting inside it and those starting outside it are attracted to.
There’s a full lecture by Steven Strogatz here on the Van der Pol oscillator which is very good, though you don’t need to know all of the details for this course.