MAM2046W - Second year nonlinear dynamics

Section 2.2: Ruling out closed orbits

​
Strap in, things are about to get mathsy! We’re going to get into some slightly more complicated mathematical notation than we have before. You should have seen all of it, but I’ll try and explain it as well as possible as we go along.
​
Remember back last year we were able to show that dynamical systems in one dimension (ie. first order, no time-dependence) could not have oscillations?
​
We are going to prove something similar in two dimensions for a particular class of systems.
​
We already know that there do exist systems in two dimensions which do oscillate - ie. they have closed orbits. It turns out that a dynamical system in two dimensions which can be written in a particular way can never have closed orbits.
​
A system which can be written as:

x
=-
∂
x
V(x,y)

y
=-
∂
y
V(x,y)
for some
V(x,y)
cannot have closed orbits. We can actually write this in vector notation as:

x
=-∇V(x,y)
where ∇=(
∂
x
,
∂
y
).
​
Such systems are called gradient systems as ∇ is the gradient operator, and when applied to a function gives a vector which is the gradient of the function in the basis directions.
​
It can be stated that a gradient system cannot have closed orbits.
​
To prove this, let’s assume that we have a system which is a gradient system, but there is a closed orbit. Moving along the closed orbit, the value of the potential will change, but if we start and end at the same point, then the total change in the potential,
ΔV
, must be zero, as the potential is just a single-valued function of
xandy
.
​
If you walk a little way along the path (say from time 0 to time t) of the closed orbit, you can calculate how much V has changed by doing a path integral:
ΔV=
t
∫
0
dV
dt
t
If you walk around the whole path, which has, say period
T,then
this will give
ΔV=
T
∫
0
dV
dt
t
which we know from the above argument has to be zero on the left hand side. But let’s look at the right hand side. V itself is a function of
xandy
which along a path are themselves functions of t, so we can write:
dV
dt
=
∂V
∂x
dx
dt
+
∂V
∂y
dy
dt
=
∂
x
V

x
+
∂
y
V

y
=∇V.

x
so the above integral is
ΔV=
T
∫
0
(∇V.

x
)t
but for a gradient system we have that

x
=-∇V(x,y)
so that:
ΔV=-
T
∫
0
(

x
.

x
)t=-
T
∫
0

|x
2
|
t
where remember

x
isthe
vector rate of change of
xandy
along the path. So long as we aren’t at a fixed point, then this can’t be zero, and therefore because we have a square on the right hand side inside the integral, the right hand side can’t be zero. But we know that the left hand side is zero, so we have a contradiction. So it is impossible to have a path (which isn’t just a trivial fixed point) for which
ΔV=0
which rules out any closed orbits in a gradient system.
​
Now we can look at an example and prove that because it is a gradient system, it can’t have closed orbits. For instance:

x
=siny

y
=xcosy
This can clearly be written like

x
=-∇V(x,y),forV=-xsiny
​
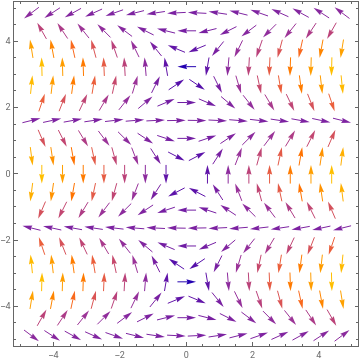
Plotting the vector field for this example we see
In[]:=
VectorPlot[{Sin[y],xCos[y]},{x,-5,5},{y,-5,5}]
Out[]=
Which in this part of the phase plane doesn’t have any closed orbits, and you should be able to convince yourselves that in fact in no part of the phase plane could it have any (look at the periodicity in the y-direction in the phase plane, and what happens as you scale
x.
​
In general if we have a system of the form

x
=f(x,y)

y
=g(x,y)
Then if this is a gradient system we can ‘partially’ integrate:
-
∂
x
V(x,y)=f(x,y)
-
∂
y
V(x,y)=g(x,y)
And if these both give the same
V(x,y)then
we have a gradient system. Try this with

x
=
2
y
+ycosx

y
=2xy+sinx
Note that we have said that being a gradient system implies that there are no closed orbits, but we haven’t said anything about the implication the other way. There can indeed be non-gradient systems which also have no closed orbits, and this can often be proved in a similar way.
​
Take the example

x
=y

y
=-x-
3
y
This is clearly not a gradient system, but we can write an energy function (you shouldn’t be able to see this from the above equations immediately):
E=
1
2
(
2
x
+
2

x
)=
1
2

2
x
+
2
y

where

E
=x

x
+y

y
=xy+y-x-
3
y
=-
4
y
=-
4

x
<=0
and it’s only zero for a fixed point.
​
What this means is that for any trajectory which isn't a fixed point, the energy of our system is decreasing. In fact this is the dynamical system for a damped harmonic oscillator
(

x
+
3

x
+x=0)
, so it makes sense that the energy of the system always decreases.
​
Considering a closed cycle (we will use closed cycle/orbit interchangeably) in this system
ΔE
around the cycle must be zero, for the same reason as with ΔV above. We can write the change as:
ΔE=
T
∫
0

E
t=-
T
∫
0
4

x
t<=0
So we have that
ΔE=0
and
ΔE<=0
which is a contradiction, so we can’t have closed cycles in this system.
​
Liapunov/Lyapunov functions
​
This is the first time in this course, or the previous one we have mentioned the name Lyapunov, but it will come up a number of times as we go on, in particular when we get on to chaos.
​
In the previous example we were able to show the absence of closed cycles by finding an energy function which always decreased along non-fixed-point trajectories. In fact we can generalise this that any system for which we can find a positive function,
V(x)
, of the phase space coordinates away from a fixed point at
*
x
:
V(x)=
>0,forx!=
*
x
0,forx=
*
x
and where the rate of change of
V(x)isnegativealongtrajectories:

V
=
<0,forx!=
*
x
0,forx=
*
x
then we can say that there are no closed orbits and
*
x
willbe
globally asymptotically stable. This means that wherever you start in this system, you will always end up at
*
x
. That is:
x(t)->
*
x
ast->∞
​
​
As a true aside, there is something similar that shows up in high energy theoretical physics (in particular quantum field theory) called a c-theorem, but we are not going to go into that here...
​
Dulac’s criterion
​
We’re going to show one other way to prove that a system can’t have any closed orbits.
​
To show this we will have to use Green's theorem. I’m going to write it out in words, which is going to seem super complicated, but we will break it down after and see what it means:
​
​
This last part means that we take the vector at the boundary, and take the component of it in the direction normal to the boundary and then integrate that along the boundary - moving counterclockwise.
​
​
which in 2d is equal to
ie. is a scalar quantity. The integral of this over some region in 2d is:
​
​
Let’s just look at a quick example of this. Taking the vector field
and taking some region given in blue below, we plot the vector field, some region R, and the unit normal to the boundary of the region given by the black arrows:
​
The scalar field
Which we now overlay on top of the above plot as a heat map (ie the colours indicating values between -1 and 1).
​
OK, so that’s Green’s theorem, which is incredibly powerful, but we aren’t going to prove it here. It’s probably a lot to take in so don’t stress about it too much for the moment. We are however going to use it.
​
Now on to Dulac’s criterion
​
Let’s say that we have some vector field describing a dynamical system
​
​
Note for a moment in the above expression which things are vectors and which are scalars. We can write it out purely in terms of scalars as:
​
​
​
​
The right hand side can be written as:
​
​
​
Given a vector field:
If you take
​
​
Note that naively it looks like there might be closed orbits, but zooming into the region around the origin gives:
ie. an ingoing spiral. Check that this is the case by linearising the system.
​
What is the intuition behind Dulac’s criterion?
​
​
​
​
OK, so next we are going to move on to showing that there are closed orbits....
​
Next Page
​
Homepage