
You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
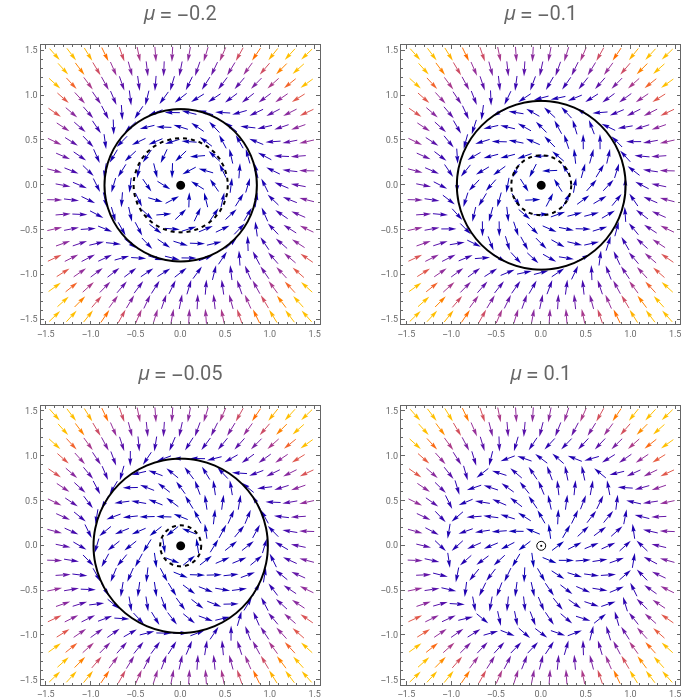 |
Subcritical Hopf bifurcation happens at μ=0 |
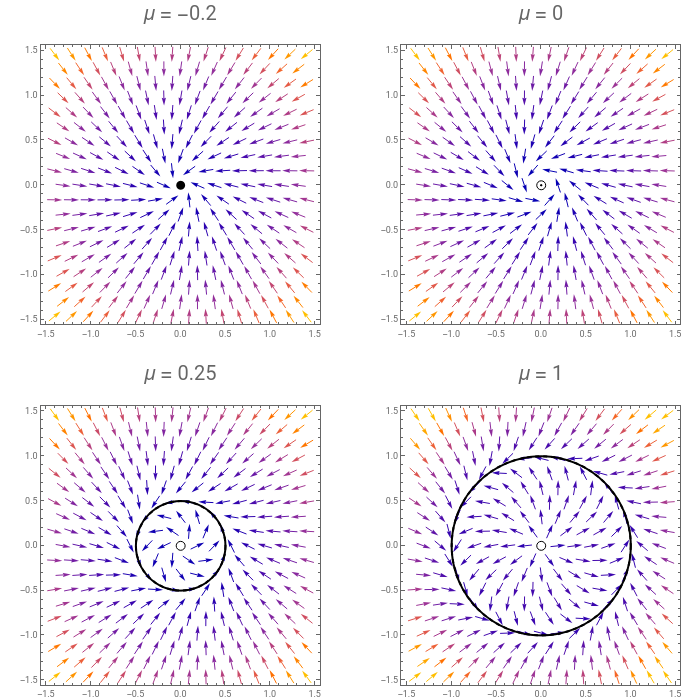 |
Supercritical Hopf Bifurcation occurs at μ=0 |
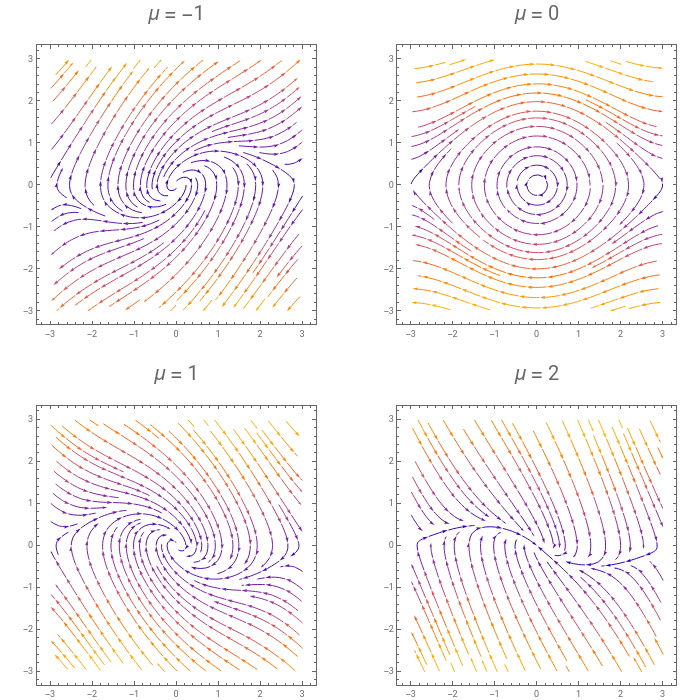 |
Degenerate Hopf bifurcation happens at μ=0.Centers appear at μ=0, before and after we have stable and unstable spirals |

You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »