MAM2046W - Second year nonlinear dynamics
MAM2046W - Second year nonlinear dynamics
Section 3.6: Poincaré maps
Section 3.6: Poincaré maps
We’re now going to introduce one of the key methods which will be needed for studying chaos later in the course. It’s a way to get a picture of what is happening in a phase portrait in potentially higher dimensional systems where just looking at the phase portrait as we have studied it so far is going to be too complicated.
We’re going to start off with an example and see how we can generalise. We’re going to take a relatively simple system, of the form:
r
2
r
θ
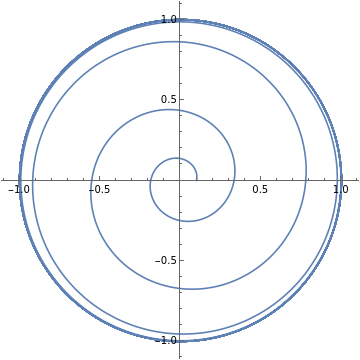
and let’s start off with initial condition . We can easily plot the trajectory for this flow as we can actually solve this system analytically:
θ(0)=0,r(0)=0.1
r=∫t⟹r(t)=(-1)+1
1
r(1-)
2
r
0.1
t
2
0.1
2t
θ
In[]:=
r[t_]=(-1)+1;θ[t_]=5t;ParametricPlot[{r[t]Cos[θ[t]],r[t]Sin[θ[t]]},{t,0,20}]
0.1
t
E
2
0.1
2t
E
Out[]=
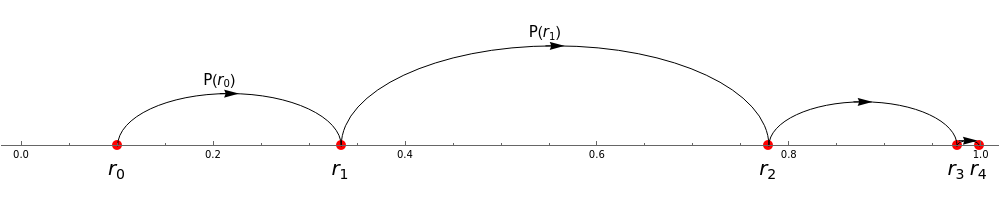
We can ask what we would see if we were just sitting on the positive x-axis. Every we would see the path whizz past again. We will call the positive x-axis the surface of section, and label it In general we will be interested in creating some surface (which in this case is actually just a line, but in higher dimensions it can be a surface, or hypersurface), and asking about how a trajectory intersects with this surface. It’s important also that the trajectories don’t flow along the surface, but pass through it. Let’s see what happens from the point of view of the surface in this case.
2π
5
S.
S
We start on the surface at position =0.1. On the next pass through, we have been travelling for time t=, so we are now at
r
0
2π
5
r
1
2π
5
0.1
2π
5
2
0.1
4π
5
On the next rotation we are at
r
2
4π
5
0.1
4π
5
2
0.1
8π
5
We define a map which takes us from to:
P
r
i
r
i+1
r
i+1
r
i
So we can imagine that this map takes a point on and maps it to a new point on
S
S:
In[]:=
p1=(-1)+1/.t->Range[0,4];points=Partition[Riffle[p1,p1][[2;;-2]],2];lab={"P()","P()","P()","P()"};ShowListPlot[{#,0}&/@p1,Axes->{True,False},PlotStyle->{PointSize[0.01],Red}],GraphicsCircle{Mean[#],0},,{0,π},GraphicsArrowheads[0.015],ArrowMean[#]-0.01,,Mean[#]+0.01,&/@points,GraphicsStyleTextlab[[#]],Mean[points[[#]]]-0.01,0.03+,15&/@Range[Length[points]-2],Show[Graphics[Style[Apply[Text,#]&/@Partition[Riffle[{"","","","","",""},{#,-0.05}&/@p1],2],20]]],AspectRatio->0.2,ImageSize->1000,PlotRange->{-0.1,0.3}
0.1
t
E
2
0.1
2t
E
2π
5
r
0
r
1
r
2
r
3
#[[2]]-#[[1]]
2
#[[2]]-#[[1]]
2
#[[2]]-#[[1]]
2
points[[#]][[2]]-points[[#]][[1]]
2
r
0
r
1
r
2
r
3
r
4
r
5
Out[]=
Clearly this will carry on forever and the points will get closer and closer together as we go around more and more times.
Congratulations, you have just seen your first Poincaré map, though this isn’t the usual way that it’s presented. This is really to make sure that we can see why it’s a map.
One could think about doing this as a cobweb diagram. To get this we need the mapping P(r) explicitly, but this is just the same as plugging in instead of 0.1 into our equation, and asking what is the position after time :
r
i
2π
5
r
i+1
r
i
2π
5
2
r
i
4π
5
So therefore:
P(r)=-1+1
2π
5
r
2
r
4π
5
Plotting this, with =0.1 we get the following cobweb diagram, where we have plotted both and we bounce between the two of them.
r
0
P(r)andr
In[]:=
p1=(-1)+1/.t->Range[0,5];Sort[Join[{{p1[[1]],0}},Partition[points=Riffle[p1,p1][[2;;-2]],2],Partition[points=Riffle[p1,p1[[2;;]]][[2;;-2]],2]]];ShowPlot-1+1,r,{r,0,1.5},PlotRange->{0,1.5},AxesLabel->Evaluate[Style[#,20]&/@{"","=P()"}],Graphics[{Red,Thick,Line[%]}],Graphics[{Red,Thick,Arrow[%[[;;4]]]}],ImageSize->500,AspectRatio->1
0.1
t
E
2
0.1
2t
E
2π
5
r
2π
5
E
2
r
4π
5
E
r
i
r
i+1
r
i
Again, this is an illustration of the Poincaré map for this system.
Let’s take a step back and think about what we’ve got here. We took a system where we could define some surface (in this case actually a line) where the trajectories passed through. It happened to be in a relatively simple periodic way in this case, but it doesn’t have to be. We could then define something about the relative positions that the trajectory passed through the surface. This is the map from one pass through to the next, and is what we call the Poincaré map. Each point on the surface gets mapped to another point on the surface. We saw that there was a fixed point on the map, and this corresponds to the stable limit cycle.
Let’s look at another example, this time of the driven system:
for some positive driving frequency ω. We can turn this into a two-dimensional autonomous system given by:
So more generally:
This whole system actually models a sinusoidally forced resistor-capacitor system, and what the stable limit cycle tells us here is that it we will move towards a regular forced oscillation, however the system may have started off.
Stability of the limit cycle
OK, now taking this and plugging it into the above equation we have:
Remember that the right hand side was essentially a matrix operation on the starting vector (away from the fixed point). We can do this again to get:
and in fact we can iterate it any number of times to get:
We can think of the Floquet multipliers as telling you how quickly a small perturbation from the orbit will grow or shrink. When you are in higher dimensions, it also tells you the direction that you will be growing/shrinking. Thus, for a two dimensional system, with a one dimensional surface of sections, we have a single Floquet multiplier which tells us how fast we will move towards/away from the limit cycle. In fact, in that case the Floquet multiplier will just be given by:
We have to be very careful here not to get confused with the normal type of linear stability analysis where we have some instability growing or shrinking exponentially. Remember we have a map here which can be thought of as a discrete set of steps. The λ tells you about how you grow each time you pass through the surface, so these are a discrete set of jumps. Let’s go back to the case above and start close to the limit cycle:
The Floquet multiplier in this case is:
then on the next iteration we will be at
and on the next at
Looks good to me!
In fact in this case, because the Poincaré map is a straight line, the linearisation is exact for any starting value.
So just don’t think that the linear term gives you some continuous time behaviour of perturbations away from or towards the fixed point, we are talking about iterated maps here.