​
Solving equations

(*1*)​​Solve[x^2+2x-5==0,x]
Out[]=
{x-1-
6
},{x-1+
6
}
In[]:=
​​Solve[x^2+1*y-5==0,y]
Out[]=
{{y5-
2
x
}}
In[]:=
Solve[x^2+ax-a^2==0,x](*withparameters*)​​Solve[x^2+ax-a^2==0,a]
Out[]=
x
1
2
(-a-
5
a),x
1
2
(-a+
5
a)
Out[]=
a
1
2
(x-
5
x),a
1
2
(x+
5
x)
In[]:=
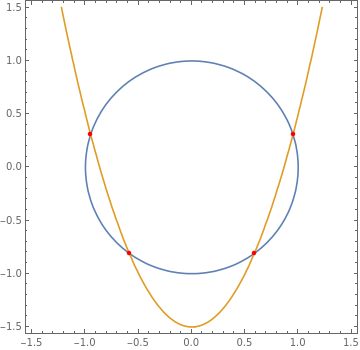
pts=Solve[x^2+y^2==1&&y-2x^2+3/2==0,{x,y}](*systemofequations:intersectionpointsofacircleandaparabola*)
Out[]=
x-
1
2
1
2
(5-
5
)
,y
1
4
(-1-
5
),x
1
2
1
2
(5-
5
)
,y
1
4
(-1-
5
),x-
1
2
1
2
(5+
5
)
,y
1
4
(-1+
5
),x
1
2
1
2
(5+
5
)
,y
1
4
(-1+
5
)
In[]:=
​​Show[{ContourPlot[{x^2+y^2==1,y-2x^2+3/2==0},{x,-1.5,1.5},{y,-1.5,1.5}],Graphics[{Red,PointSize[Medium],Point[{x,y}/.pts]}]}]
Out[]=
In[]:=
​​Solve[(x^4-1)(x^4-4)==0,x,Complexes]​​Solve[(x^4-1)(x^4-4)==0,x,Reals]​​Solve[(x^4-1)(x^4-4)==0,x,Integers]
Out[]=
{x-1},{x-},{x},{x1},{x-
2
},{x-
2
},{x
2
},{x
2
}
Out[]=
{x-1},{x1},{x-
2
},{x
2
}
Out[]=
{{x-1},{x1}}

​
Derivative

In[]:=
f[x_]:=Sin[x^2]+Exp[-4x]​​f[x]
Out[]=
-4x

+Sin[
2
x
]
In[]:=
f'[x]
Out[]=
-4
-4x

+2xCos[
2
x
]
In[]:=
D[f[x],x]
Out[]=
-4
-4x

+2xCos[
2
x
]
In[]:=
g[x_,y_]:=Sin[x^2]+Exp[-4y]​​g[x,y]
Out[]=
-4y

+Sin[
2
x
]
In[]:=
g'[x,y]
Out[]=
′
g
[x,y]
In[]:=
D[g[x,y],x]​​D[g[x,y],y]
Out[]=
2xCos[
2
x
]
Out[]=
-4
-4y


​
Differentional equations

In[]:=
DSolve[y'[x]+y[x]==4Sin[x],y[x],x]
Out[]=
{{y[x]
-x


1
+2(-Cos[x]+Sin[x])}}
In[]:=
​​DSolve[y''[x]+2y'[x]==Exp[-x],y[x],x]
Out[]=
y[x]-
-x

-
1
2
-2x


1
+

2

In[]:=
​​DSolve[{y'[x]+y[x]==4Sin[x],y[0]==0},y[x],x](*withboundaryconditions*)
Out[]=
{{y[x]-2
-x

(-1+
x

Cos[x]-
x

Sin[x])}}
In[]:=
​​DSolve[y'[x]+xy'[x]^2==1,y,x](*nonlineardifferantialequation*)
Out[]=
yFunction{x},

1
+
1
2
2
1+4x
-2ArcTanh[
1+4x
]-Log[x],yFunction{x},

1
+
1
2
-2
1+4x
+2ArcTanh[
1+4x
]-Log[x]
In[]:=
DSolve[{2y'[x]+z'[x]==4z[x]-x,y[x]-z[x]==-4},{y[x],z[x]},x](*systemsoflinearequations*)
Out[]=
y[x]-
4
3
+6
1
864
(-357+36x)+
4x/3


1
,z[x]
8
3
+6
1
864
(-357+36x)+
4x/3


1

In[]:=
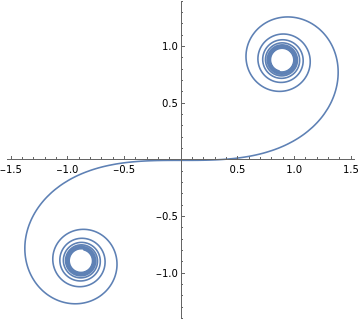
DSolve[{x'[s]==Cos[t[s]],y'[s]==Sin[t[s]],t'[s]==s,x[0]==0,y[0]==0,t[0]==0},{x,y,t},s];(*Cornuspiral*)
In[]:=
ParametricPlot[Evaluate[{x[s],y[s]}/.%],{s,-10,10}]
Out[]=

​
Integral

In[]:=
Integrate[x^2+Sin[x],x](*integral*)
Out[]=
3
x
3
-Cos[x]
In[]:=
Integrate[1/(x^3+1),{x,0,1}](*definiteintegral*)
Out[]=
1
18
2
3
π+Log[64]
In[]:=
​​Integrate[1/(x^3+1),{x,0,1}](*Integralsinterpretationistheareabeneeththeplot*)​​Plot[1/(x^3+1),{x,0,1},FillingAxis]
Out[]=
1
18
2
3
π+Log[64]