498 Example: Showing 7 is a Congruent Number via Addition on an Elliptic Curve over the Reals

From Ezra Brown's paper Three Fermat Trails to Elliptic Curves, we have the following Key Lemma: n is a congruent number if and only if there exists a rational point on the elliptic curve
2
y
=
3
x
-
2
n
x
such that x is a rational square with even denominator. Recall that a rational number n is said to be congruent if there exists a right triangle with rational sides (including hypotenuse) whose area is n. Using the idea of elliptic curve addition, here is a way to show that n = 7 is a congruent number and find a rational right triangle whose area is 7. The code below can be modified to check if any other rational number n is congruent.
In[]:=
Clear[n,x,X,Y,Z]
In[]:=
n=7;

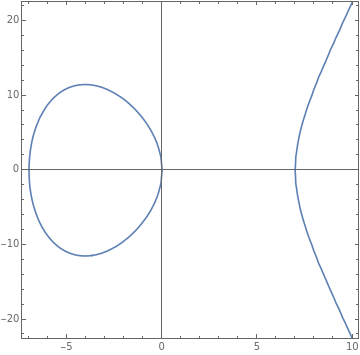
Plot the elliptic curve
2
y
=
3
x
-
2
n
x

In[]:=
ContourPlot[
2
y

3
x
-
2
n
x,{x,-10,10},{y,-25,25},AxesTrue,AspectRatio1,PlotRange{-25,25}]
Out[]=

Define Elliptic Curve Addition Algebraically with ∞ = {∞,∞}

In[]:=
EllAdd[xP_,yP_,xQ_,yQ_,n_]:=IfxP∞,{xQ,yQ},IfxQ∞,{xP,yP},​​IfxPxQ&&yP-yQ,{∞,∞},IfxP==xQ&&yP==yQ,​​
2
3
2
xP
-
2
n
2yP
-2xP,-yP+
3
2
xP
-
2
n
2yP
xP-
2
3
2
xP
-
2
n
2yP
-2xP,
2
yQ-yP
xQ-xP
-xP-xQ,-yP+
yQ-yP
xQ-xP
xP-
2
yQ-yP
xQ-xP
-xP-xQ​​
Find a rational point on the elliptic curve by testing points with rational x-coordinate to see if the corresponding y-coordinate is rational. To get the y-coordinate, solve the elliptic curve equation for y, to get y = g(x), i.e. y =
±
3
x
-
2
n
x
. Here, n = 7. As an example, there are rational x - values that lead to rational y - values of zero!
In[]:=
g[x_]:=
3
x
-49x
In[]:=
Solve[g[x]0,x]
Out[]=
{{x-7},{x0},{x7}}
Let's try with integer values for x, starting with x = -7 up to x = 0 for the left part of the elliptic curve!
In[]:=
TableForm[Table[{x,g[x]},{x,-7,0}],TableHeadings->{None,{"x","y = g(x)"}}]
Out[]//TableForm=
x
y = g(x)
-7
0
-6
78
-5
2
30
-4
2
33
-3
2
30
-2
3
10
-1
4
3
0
0
Now let's try the right half of the elliptic curve, with integer values from x = 7 to x = 30.
In[]:=
TableForm[Table[{x,g[x]},{x,7,30}],TableHeadings->{None,{"x","y = g(x)"}}]
Out[]//TableForm=
x
y = g(x)
7
0
8
2
30
9
12
2
10
510
11
6
22
12
2
285
13
2
390
14
7
42
15
4
165
16
12
23
17
4
255
18
15
22
19
2
1482
20
6
195
21
14
42
22
9570
23
4
690
24
2
3162
25
120
26
16302
27
6
510
28
14
105
29
6
638
30
25530
Check to make sure the point (25,120) is on the elliptic curve. If so, then find more rational points on this elliptic curve by using elliptic curve addition to add the point to itself. If we find a rational point such that the x-coordinate is a perfect square with even denominator, then by the Key Lemma, we know that 7 is a congruent number. Also, from Brown's paper, the rational right triangle (i.e. all sides are rational, including the hypotenuse) that has area 7 will be given by
{X,Y,Z}={
x+7
-
x-7
,
x+7
+
x-7
,2
x
}
.
In[]:=
2
120

3
25
-49*25
Out[]=
True
In[]:=
P={25,120}
Out[]=
{25,120}
In[]:=
P=EllAdd[P[[1]],P[[2]],P[[1]],P[[2]],n]
Out[]=

113569
14400
,
17631503
1728000

In[]:=
P[[1]]
Out[]=
337
120
Since the x-coordinate of the rational point on the elliptic curve is a perfect square with even denominator, it follows from the Key Lemma that 7 is congruent!
In[]:=
x=P[[1]]
Out[]=
113569
14400
Find the sides of the rational right triangle whose area is 7.
In[]:=
{X,Y,Z}=
x+n
-
x-n
,
x+n
+
x-n
,2
x

Out[]=

35
12
,
24
5
,
337
60

In[]:=
2
X
+
2
Y

2
Z
Out[]=
True
In[]:=
1
2
X*Y
Out[]=
7