You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
PLAY Interpolation !
PLAY Interpolation !
Mit diesem Modul untersuchen wir das Verhalten von Interpolationspolynomen. Wir wollen eine gegebene Funktion auf einem Intervall durch ein Polynom möglichst gut approximieren. Die Funktion könnte beispielsweise sehr kompliziert sein oder durch experimentelle Daten gegeben sein, so daß uns nur wenige Auswertungen an bestimmten Stützstellen ,,...,∈[a,b] vorliegen. Aus den Wertepaaren wird nun Polynom (x) berechnet - der sogenannte Interpolant.Der Fehler des Interpolanten lässt sich darstellen durch die Formel wobei die n+1-te Ableitung von ist und ausgewertet wird an einer bestimmten (unbekannten) Zwischenstelle ∈[a,b]. Die Funktion ist ein Polynom, welches nur von den Positionen der Stützstellen abhängt.Die Frage ist nun unter welchen Umständen wir mit (x) eine besonders gute Approximation für unsere Funktion erhalten? Offenbar können wir den Fehler klein halten, in dem wir Stützstellen wählen, durch welche die Funktion einen minimalen Wert annimmt. Der tatsächliche Fehler hängt dann aber noch von der n+1-ten Ableitung von ab.Auf dem Spielfeld unten lässt sich dieser Umstand interaktiv verstehen.
f:[a,b]
f
x
0
x
1
x
n
(,f()),i=0,1,...n
x
i
x
i
p
n
f(x)-(x)=ω(x)()
p
n
1
(n+1)!
(n+1)
f
ξ
x
(n+1)
f
f
ξ
x
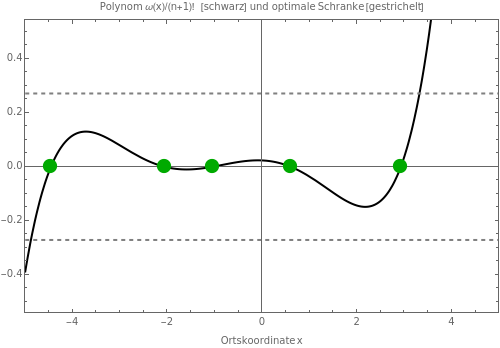
ω(x)
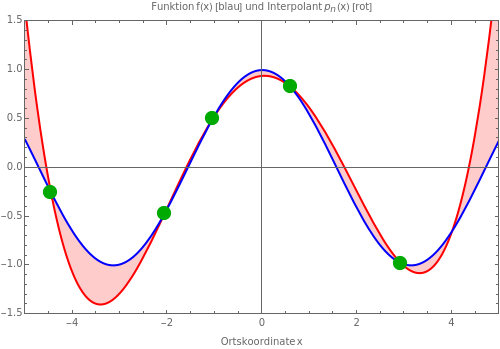
p
n
f(x)
ω(x)
f
Out[]=
| |||||||||||||||||||||
◼ Im Modus ‘frei’ kannst du in beiden Plots die Position der Stützstellen beliebig verschieben.
Gelingt es dir Stützstellen zu finden, bei denen das Polynom nur Werte innerhalb des optimalen Bereichs (gestrichelte Linien) annimmt?
Deine Stützstellen kannst du mit den tatsächlich optimalen Positionen (Tschebyscheff-Stützstellen) im Modus ‘optimal’ vergleichen.
◼ Offenbar werden verschiedene Funktionen selbst mit optimalen Stützstellen nicht gleich gut approximiert.
Findest du zu einer festen Funktion Stützstellen, die einen kleineren Fehler erzeugen als Tschebyscheff-Stützstellen?
In der oberen rechten Ecke wird der integrale (-)Fehler sowie die maximale Abweichung für den aktuellen Fall angezeigt.
Gelingt es dir Stützstellen zu finden, bei denen das Polynom
ω(x)
Deine Stützstellen kannst du mit den tatsächlich optimalen Positionen (Tschebyscheff-Stützstellen) im Modus ‘optimal’ vergleichen.
◼ Offenbar werden verschiedene Funktionen selbst mit optimalen Stützstellen nicht gleich gut approximiert.
Findest du zu einer festen Funktion Stützstellen, die einen kleineren Fehler erzeugen als Tschebyscheff-Stützstellen?
In der oberen rechten Ecke wird der integrale (
1
L
© M.Torrilhon / M.Frank (2013)