You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
Out[]=
PLAY Komplexe Ebene !
PLAY Komplexe Ebene !
IndiesemModulbetrachtenwirZahleninderkomplexenEbene,alsoZahlenderFormz=x+y∈wobei=.Hierbeigilt,dassr=|z|=Abs(z)ist.ImModus'mitnWurzelnderkomplexenZahl'betrachtenwirdiePolynomgleichung=zfürw,z∈undeinenfestenWertn∈,n≥1undfragenuns,welcheLösung(en)dieseGleichungüberhat.AusderlinearenAlgebrawissenwir,dassdasPolynom-z=0höchstensnNullstellenhabenkann.AberwiesehendieLösungenw∈aus,sodass=zerfülltist?DieslässtsichaufdemSpielfelduntensowohlgrafischalsauchinZahlendarstellen.
-1
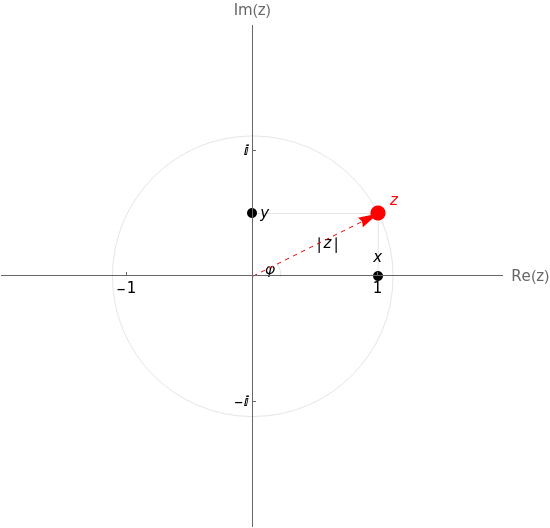
undx,y∈.ImModus'komplexeZahl'wirdfüreinebeliebigeZahlz∈ihrRealteil(Re(z)=x),ihrImaginärteil(Im(z)=y)undihrabsoluterWertangezeigt.AußerdemwirddasArgumentvonzberechnet,alsoderWinkelφderinderDarstellungvonzinPolarkoordinatenvorkommt,alsoz=rφ
n
w
n
w
n
w
Out[]=
| ||||||||||||||||||||||||
© M.Torrilhon / B.Schmidtmann (2014)