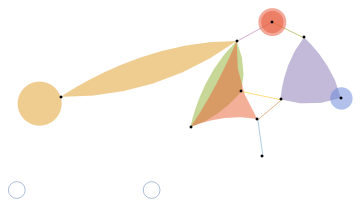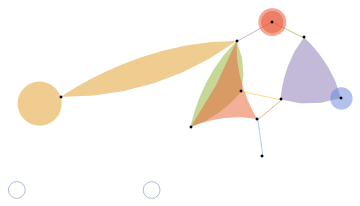Basic Examples 
(5)
 

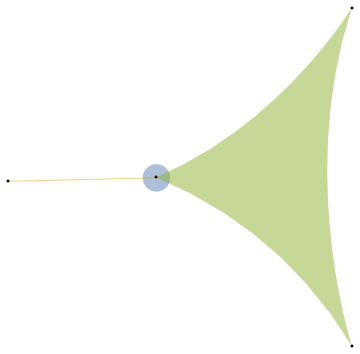
Symmetries:
In[209]:=
h=
Hypergraph
@{{1},{1,2},{1,3,4}}
Out[209]=
In[212]:=
EdgeSymmetry[h]
Out[212]=
{{1}{},{1,2}{Cycles[{{1,2}}]},{1,3,4}{Cycles[{{1,2}}],Cycles[{{1,3}}]}}
———
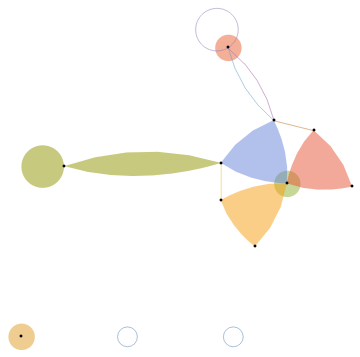
Hypergraph:
In[268]:=
h1=
RandomHypergraph
[{10,{{2,0},{3,1},{5,2},{4,3}}}]
Out[268]=
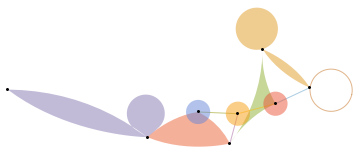
In[269]:=
h2=
RandomHypergraph
[{10,{{2,0},{3,1},{5,2},{4,3}}}]
Out[269]=
In[270]:=
h1+h2
Out[270]=
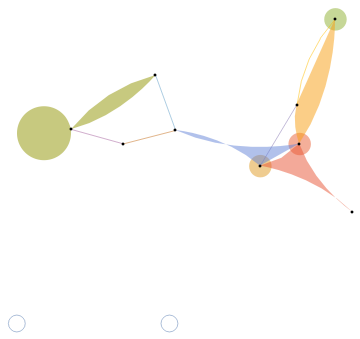
In[271]:=
h1**h2//TraditionalForm
Out[271]//TraditionalForm=
———
Hypergraph adjacency tensor:
In[272]:=
hg=
CanonicalHypergraph
@
RandomHypergraph
[{10,{{2,0},{3,1},{5,2},{4,3}}}]
Out[272]=
In[273]:=
AdjacencyTensor
@%
Out[273]=
SparseArray
Specified elements: 12
Dimensions: {11,11,11}

In[274]:=
CanonicalHypergraph
@
AdjacencyHypergraph
[%]
Out[274]=
In[241]:=
IsomorphicHypergraphQ[%,%%%]
Out[241]=
True
———
Hypergraph incidence matrix:
In[242]:=
CanonicalHypergraph
@
RandomHypergraph
[{10,{{2,0},{3,1},{5,2},{4,3}}}]
Out[242]=
In[243]:=
HypergraphIncidenceMatrix
@%
Out[243]=
SparseArray
Specified elements: 22
Dimensions: {8,14}

In[244]:=
CanonicalHypergraph
@
IncidenceHypergraph
[%]
Out[244]=
HyperMatrix: