WOLFRAM NOTEBOOK

Wolfram quantum framework for analog QPUs: QuEra Aquila case

Wolfram Quantum Team
quantum AT wolfram.com
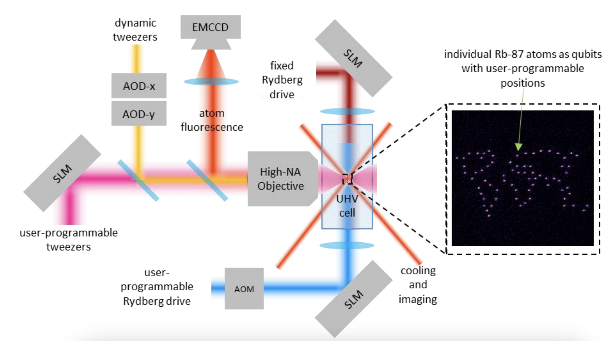
Analog quantum processing units (quantum annealers) use continuous variables for optimization tasks, such as finding global minima. Gate-based quantum computers use discrete quantum gates to manipulate qubits for versatile quantum algorithms, including factorization, simulation, and optimization. One example of analog Quantum Processing Units (QPUs) is Aquila, which is a neutral-atom QPU from QuEra Computing, with up to 256 qubit. Aquila is also available on Amazon Braket, which is accessible using AWS service connect from a Wolfram notebook. In this computational essay, we will focus on some examples from QuEra's recent white paper, and do the simulation using quantum functionalities of Wolfram quantum framework, and also show how to send queries to Aquila, using Amazon Braket.
The Hamiltonian for QuEra system of atoms is given by (after RWA):
H(t)
∑
j
Ω
j
(t)
2
i
ϕ
j
(t)
e
g
j
r
j
+
-i
ϕ
j
(t)
e
r
j
g
j
|-
∑
j
Δ
j
(t)
n
j
+
∑
j<k
V
jk
n
j
n
k
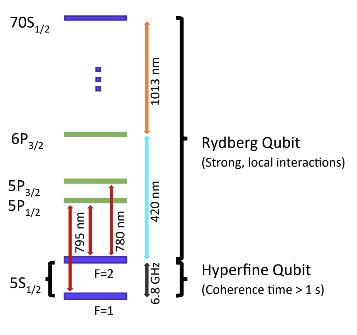
where
Ω
is the the Rabi frequency,
ϕ
the laser phase, and
Δ
the detuning of the driving laser field coupling the ground states
g
j
and excited Rydberg state
r
j
of the j-th atom.
V
jk
C
6
x
j
-
x
k
6
|
represents the van der Waals interaction between atom-j and atom-k, while is
n
j
r
j
r
j
the number operator of j-th site (more info on actual values of
C
6
can be found in QuEra webpages).
We have defined the corresponding Hamiltonian as follows:
AquilaHamiltonian[sites, {Ω, Δ, ϕ}]
, where it takes sites as a list of atom positions,
{{
x
1
,
y
1
},{
x
2
,
y
2
},...}
, with each position in μm,
Ω
is the the Rabi frequency,
ϕ
the laser phase, and
Δ
the detuning of the driving laser field.

Setup

Single atom

Let’s consider the single atom dynamics.

Rabi Oscillation (Ω=constant, Δ=0 and ϕ=0)

Ramsey Protocol (Ω as two pulses, Δ=constant, ϕ=0)

Floquet Protocol (Ω=const., Δ=const. Sin[ω t], and ϕ=0)

Spin echo

Two atoms

Multi-atoms: ordered phases

Multi atoms: Blockaded Rabi Oscillations

Multi atoms: quantum scars

Maximum independent set on unit disk graphs

This part is related to Section 6 of the QuEra white paper.
Let’s first analyze the Maximum independent set on unit disk graphs, classically.
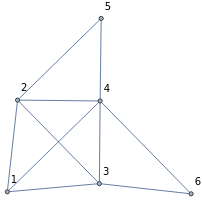
Create a King’s graph with a 30% random dropout:
In[]:=
SeedRandom[1337];​​kingGraph=VertexDelete[#,RandomSample[VertexList[#],Round[.3VertexCount[#]]],VertexCoordinates->AssociationThread[VertexList[#],GraphEmbedding[#]]]&@DiskGraph[3];
Show the King’s graph:
In[]:=
labels=Thread[VertexList[kingGraph]->Range[Length@VertexList[kingGraph]]];​​Graph[kingGraph,VertexLabelslabels]
Out[]=
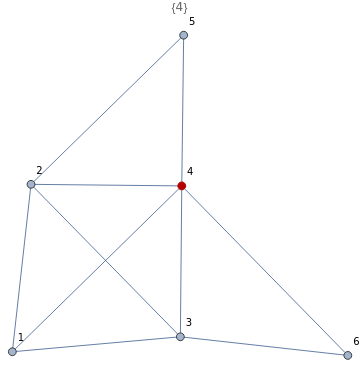
Find an independent vertex set of the King’s graph with a maximum number of vertices:
In[]:=
mis=Lookup[labels,#]&/@FindIndependentVertexSet[kingGraph,Infinity,All]
Out[]=
{{1,5,6},{2,6},{3,5},{4}}
Highlight them in the graph:
In[]:=
ListAnimate[Table[HighlightGraph[kingGraph,VertexList[kingGraph][[i]],VertexLabels->labels,PlotLabel->i],{i,mis}]]
Out[]=
Now, using a quantum algorithm, we will try to find those max independent vertices (in our case, it will be qubits 1, 3, 7 and 8, in a quantum system with 11 qubits).
Create the corresponding 2D lattice, with the distance of 5μm
In[]:=
sitesKG=5.VertexList[kingGraph];
Create the corresponding parameters of the Hamiltonian and plot them:
In[]:=
{Ω,Δ,ϕ}=AquilaDrive[{0,.3,1.9,tf=2.2},{0,15,15,0},{-30,-30,80,80},{0}];​​Plot[Evaluate@{Ω,Δ,ϕ},{t.,0,tf},PlotRange->All,PlotLegends->{"Ω","Δ","ϕ"}]
Find the time-dependent quantum state:
Final Rydberg population per site at a given time:
Let’s calculate if all maximal independent sets have high probability in quantum version. To do so, we will multiply their Rydberg population as a measure. If quantum algorithm works fine, then the measure for that set should be close to one (or high enough). If not, then it means we won’t be able to find some solutions.
Using classical results, visualize what maximal independent sets are more likely to be obtained from quantum algorithm:
Plot Rydberg population per sites over time:
Final Rydberg population

AWS

In this section, we will send a query to QuEra Aquila, using Amazon Braket.
Site population:
Bit-string population
Send the job to QuEra Aquila:
Given preSequence with all 1 (meaning the initial preparation was done correctly)
[make sure I understand what does that mean, given the preSequence are not all 1111...]
Different of population between theory and experimental values for each site

Initialization

Install quantum paclet:
Function to generate Analog Hamiltonian Simulation (AHS) for Braket:
Wolfram Cloud

You are using a browser not supported by the Wolfram Cloud

Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.


I understand and wish to continue anyway »

You are using a browser not supported by the Wolfram Cloud. Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.