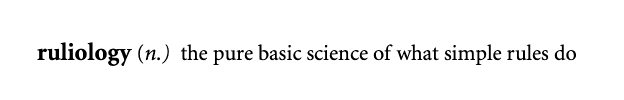Introduction to the Wolfram Model and Ruliology

Hatem Elshatlawy

Wolfram Research

Ruliology

Ruliology, is a term that is coined by Stephen Wolfram, which means the pure basic science of what simple rules do and how different rules can lead to diverse and complex behaviors.

WPP High-level Overview Summary

WPP Backstory & NKS Summary

When Stephen was writing a new kind of science studying the computational paradigm, and the computational universe of simple programs. He identified two key empirical observations:

Pattern matching and substitution is a minimal model for almost everything.

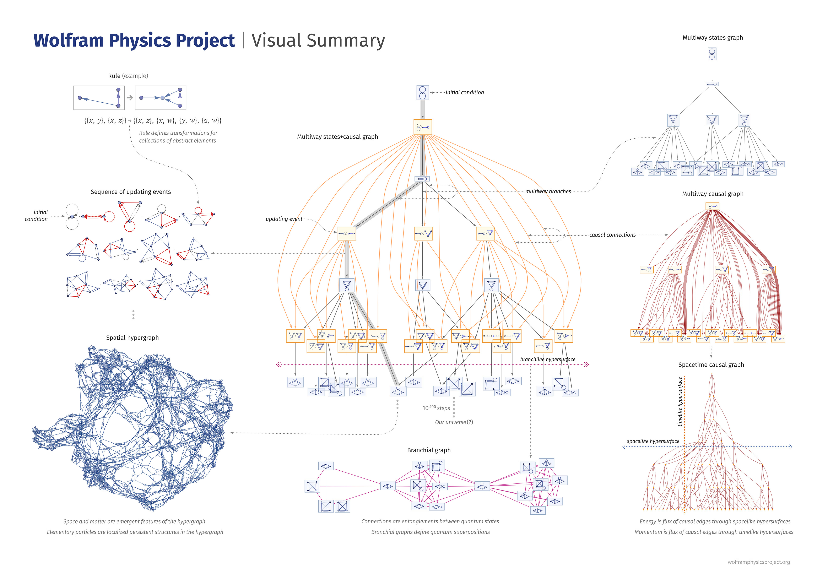
High-level overview summary of the Wolfram Model

Here, we think of the evolution of this model as corresponding to a computation, where the system starts from an initial state, follows its rules, in effect carrying out a computation to generate a sequence of states.

Out[]=

Each (directed) hyperedge corresponds to an (ordered or an unordered) relation between abstract elements, allowing us to represent the hypergraph itself as an finite collection of such relations.

Figure: A hypergraph transformation rule , represented internally as a set substitution system {{x,y},{y,z}}{{w,y},{y,z},{z,w},{x,w}}.

The dynamics of a Wolfram model system are then defined in terms of rewriting rules.

Figure: The hypergraphs obtained during the first 10 steps of evolution of the set substitution system {{x,y},{y,z}}{{w,y},{y,z},{z,w},{x,w}}

Figure: The hypergraph obtained after 14 steps of evolution of the set substitution system {{x,y},{y,z}}{{w,y},{y,z},{z,w},{x,w}}

The Wolfram model represents a discrete framework that proposes structures such as continuous spacetime geometries which may potentially emerge from large-scale limits of the underlying discrete structures. Furthermore, the evolution of these structures is dictated by various forms of rewriting rules, such as those based on graphs, hypergraphs, or strings. To illustrate this, a Wolfram model hypergraph can be represented abstractly as a finite collection of ordered or unordered relations (hyperedges) between labelled nodes, as defined below.

One can then define the dynamics of a Wolfram model system in terms of hypergraph rewriting rules as follows:

At its core, the Wolfram model, is a discrete spacetime formalism in which the continuum structure of a manifold emerges as the large scale limit of a discrete causal network and the causal network is generated in a very natural and algorithmic way from diagrammatic rewriting rules.

So we’re ultimately trying to develop an explicitly computable / constructivist foundations for physics, based upon discrete spacetime.

◼

Parallels to causal set theory, causal dynamical triangulation, spin networks / spin foams in loop quantum gravity, etc.

◼

Parallels also to constructivism and intuitionism in the foundations and philosophy of mathematics.

Multiway Systems, Causal Graphs, Branchial Graphs, and the Concept of the Multicomputation

Figure: Adapted from Multicomputation: A Fourth Paradigm for Theoretical Science https://writings.stephenwolfram.com/2021/09/multicomputation-a-fourth-paradigm-for-theoretical-science/

If one looks at the history of theoretical science, one can identify just three major modeling paradigms that have been developed over the course of scientific history---each of them leading to dramatic progress.

In the ordinary computational paradigm the typical setup is to have a system that evolves in a series of steps by repeatedly applying some particular rule.

But our models (for some rules) they are not deterministic that is multiple choices of substitutions are possible, which yield different results. Usually, we just pick one possibility and ignore the rest, but the MW system explores all possible choices at once.

Starting from A, the next state has to be BBB. But now there are two possible ways to apply the rules, one generating AB and the other BA. And if we trace both possibilities we get what we call a multiway system---whose behavior we can represent using a multiway graph:

And It’s not really difficult to construct multiway system models. There are multiway Turing machines. There are multiway systems based on rewriting not only strings, but also trees, graphs or hypergraphs. There are also multiway systems based on numbers. And all kind of multiway systems.

Combinatorially, a multiway system is simply a directed, acyclic graph of states, determined by abstract rewriting rules that inductively generate a (potentially infinite) multiway evolution graph, together with a partial order on the rewrite rule applications, determined by their causal structure.

Causal Graphs

States are connected through events. But how are events connected? Given two events the key question to ask is whether they are causally related. Does one event depend on the other—in the sense that all or part of its input comes from the output of the other event?

If we want to focus on causal relationships, we can get a multiway causal graph that represents possible causal relationships between events. We can add this dependency information to the evolution graph by putting orange lines between events that are causally related:

A “causal network”, is a directed, acyclic graph in which every vertex corresponds to an application of an update rule (i.e. an update “event”), and in which the directed edge A → B exists if and only if:

In (B) ∩ Out (A) = ∅

i.e. the input for event B makes use of hyperedges that were produced by the output of event A.

Branchial Graphs

Causal graphs capture relationships between events at different steps in the evolution of a system, branchial graphs capture relationships between states on different branches at a given step.

Branchial graphs effectively show common ancestry between multiway states for; in other words, vertices A and B are connected by an undirected edge in the branchial graph if and only if they share a common ancestor C in the multiway evolution graph.

Causal Invariance

A multiway system is “causal invariant” if and only if the causal networks generated by following all paths through the multiway system are (eventually) isomorphic as directed, acyclic graphs.

Multicomputation

It’s important to emphasize that the multicomputational paradigm is at its core not about particular histories, but about the evolution of all possible histories. And in most cases it won’t have things to say about particular histories. But instead what it will describe is what an observer sampling the whole multicomputational process will perceive.

The Ruliad (A formal necessity...)

Now instead of looking at all possible ways a given rule can update these rewrite systems, imagine the structure of spaces created by applying all possible rules. Instead of just forming a multiway graph in which we do all possible updates with a given rule, we form a rulial multiway graph in which we follow not only all possible updates, but also all possible rules.

Here’s illustrative figure of rulial multiway graphs for Turing machines with various numbers of states and colors {s, k}:

This image presented can be considered as a rough, finite approximation of the Ruliad. The complete Ruliad encompasses the exploration of infinite limits across all conceivable rules, initial conditions, and steps. Here the nodes and edges are not specific to any single entity. Nodes can represent various entities such as hypergraphs, strings, or states, while the edges signify the myriad potential causal connections between those entities.

A conceptual definition of the Ruliad:

here, for example, is a rulial multiway system made with 2-state 2-color Turing machines:

As another example, consider a multiway system based on numbers, in which the rules multiply by each possible integer:

Here’s what happens starting with 1 (and truncating the graph whenever the value exceeds 100):

The pictures here can be thought of as coarse finite approximations to the ruliad. The full ruliad involves taking the infinite limits of all possible rules, all possible initial conditions and all possible steps. Needless to say, this is a very complicated thing to do.

HoTT & How to think about the Ruliad mathematically?

“Deriving” Mathematical Spaces from Paths between Paths

Multiway systems are types, the states of the MW are terms, and the rules of MW are type constructors.
paths are then proofs, homoptopies between paths are proofs of proofs and so on.
where multiway rules corresponding to type constructors, completion rules corresponding to homotopies

The Homotopy Hypothesis

The multiway evolution graph corresponding to the first 8 steps in the nondeterministic evolution history of the string substitution rule A → AB, starting from the two character initial condition AA.

Every path in this multiway evolution graph corresponds to a proof of a proposition, as shown here for the
particular case of a proof of the proposition that AA → ABBBABBB, subject to the axiom
A → AB.

A multiway evolution graph with a red highlighted path between vertices
AA and ABBBABBB, corresponding to a proof of the proposition AA → ABBBABBB, subject to the string substitution axiom A → AB

The same multiway evolution graph showing multiple highlighted paths (red and yellow) between vertices AA and ABBBABBB,
illustrating the existence of multiple proofs of the proposition AA → ABBBABBB.

In a category theory interpretation, transformations between states in the original multiway graph are like ordinary morphisms (1-morphisms). But when we’re making transformations between “proof paths”, this is like 2-morphisms. And just as we can add transformations between proofs, we can also add transformations between proofs-between-proofs, and so on. The result is that we can build up a whole hierarchy of higher and higher categories, eventually ending with an ∞-category

Grand Overview:

In a sense, the Wolfram Model provides a computational realization of pre-geometric structures in physics and the mathematical framework of HoTT provides the formal foundation for these structures

Implications of the Ruliad & The Central Role of the Observer

The ruliad contains everything that is computationally possible. So why then do we have the perception that the universe has specific laws, and that definite things happen in it?

The world seems to us the way it does because we’re observers of the kind we are. But what ultimately is an observer? And how, for example, can we make a general model of one, as we now have general models (like Turing machines) for computational systems?

As a basic physical example, consider a gas pressure sensor based on a piston. Within the gas, individual molecules move around in complicated and seemingly random ways, hitting the piston in all kinds of configurations. But the piston “reduces out” all those details, responding just to the aggregate force of all the molecules, the same one of which can be realised in potentially infinitely many ways. The main point is that we can describe what’s going on more formally by saying that “observations by the piston” identify all the different detailed configurations of molecules, preserving only information about their aggregate force, forgetting the finer details.

The crucial feature of observers seems to be that the observer is always ultimately some kind of “finite mind” that takes all the complexity of the world and extracts from it just certain “summary features” that are relevant to the “decisions” it has to make. Observers like us have two basic characteristics: first, that they are computationally bounded, and second, that they are persistent in time.

In the end, the ruliad involves infinite rules, infinite initial conditions, and infinite time. But any way of sampling the ruliad effectively involves making particular choices about how we take those infinite limits. And that’s pretty much like the fact that as entities embedded within the ruliad, we have to make particular choices about how to sample it. One can imagine an observer very different from us (say some kind of alien intelligence) who would sample different aspects of the ruliad, and deduce totally different laws...

What’s an Observer essentially, an equivalencing machine.

(Second-order cybernetics):

Second-order cybernetics is based on the idea that no science is possible from a ‘view from nowhere’ in which one can view reality unveiled as it were. One has to consider a standpoint, or perspective, or frame from which the universe is viewed. Without it (i.e. the viewer), there is no view. The Ruliad as it stands, is abstractly defined as a view from nowhere: a totality. To carry out scientific exploration in the Ruliad, we must include a system, an observer, capable of sampling the space.

QM & the sequentialization of Time

The Limits of Ruliology: The Impossibility of Seeing the Ruliad from the Outside

[Norman Rockwell, “The Art Critic”]

Philosophy is an attempt to express the infinity of the universe in terms of the limitations of language.
A. N. Whitehead

If philosophy is an attempt to express the infinity of the universe in terms of the limitations of language, Ruliology is likewise an attempt to express that infinity in the somewhat less limited framework of the representations of computationally-bounded observers that are embedded within it.

Of course, the Ruliad is not something that we could ever directly observe, and nor is it presented as such. It is an abstract entity. However, inasmuch as it is abstract, it exists as representation in the mind of an agent and so inherits the limitations.

A fundamental theory, that is this fundamental, cannot possibly be expected to make direct predictions of the sort that the critics clearly desire. But what it can do is locate them in a web of theories, and moreover it can suggest entirely new kinds of theory that would then themselves make predictions when properly worked out in the manner appropriate for less fundamental approaches. The task of physics, indeed, is to figure out where in the Ruliad we are located. Ruliology is not then, a replacement of physics, but a way of making sense of it. What we have described is, then, not a theory of physics in the ordinary at all. It is a pre-physical framework for any possible theory of physics and should not be analysed (or critiqued) in the same terms as orthodox physical theories.