1.1 Principal Component Analysis

1.1.1 Principal Component

In[]:=
X=N[{{1,2},{2.2,3},{4,10}}];X//MatrixForm
Out[]//MatrixForm=
1.
2.
2.2
3.
4.
10.
In[]:=
std[data_]:=Module[{datatr=Transpose[data]},Transpose[N[Table[Standardize[datatr[[i]]],{i,1,Length[datatr]}]]]];
In[]:=
Xstd=std[X];Xstd//MatrixForm
Out[]//MatrixForm=
-0.927173
-0.688247
-0.132453
-0.458831
1.05963
1.14708
In[]:=
MatrixPlot[Xstd]//Binarize
Out[]=
In[]:=
n=3;
In[]:=
S=(Xstd//Transpose).Xstd/(n-1);MatrixForm[S]
Out[]//MatrixForm=

1.
0.957186
0.957186
1.

In[]:=
Covariance[Xstd]
Out[]=
{{1.,0.957186},{0.957186,1.}}
In[]:=
Eigenvalues[S]
Out[]=
{1.95719,0.042814}
In[]:=
Eigenvectors[S]
Out[]=
{{-0.707107,-0.707107},{0.707107,-0.707107}}
In[]:=
pc=Xstd.Eigenvectors[S];pc//MatrixForm
Out[]//MatrixForm=
0.168946
1.14227
-0.230784
0.418101
0.0618385
-1.56038
In[]:=
MatrixPlot[pc]//Binarize
Out[]=
In[]:=
z=PrincipalComponents[Xstd];MatrixForm[z]
Out[]//MatrixForm=
1.14227
0.168946
0.418101
-0.230784
-1.56038
0.0618385
In[]:=
Map[Reverse[#]&,z]//MatrixForm
Out[]//MatrixForm=
0.168946
1.14227
-0.230784
0.418101
0.0618385
-1.56038
In[]:=
Correlation[z]//MatrixForm
Out[]//MatrixForm=

1.
0.
0.
1.

In[]:=
pc.Inverse[Eigenvectors[S]]Xstd
Out[]=
True

1.1.2 Singular Value Decomposition

In[]:=
{u,s,v}=SingularValueDecomposition[Xstd];
In[]:=
u//MatrixForm
Out[]//MatrixForm=
0.57735
0.57735
0.57735
0.211325
-0.788675
0.57735
-0.788675
0.211325
0.57735
In[]:=
s//MatrixForm
Out[]//MatrixForm=
1.97848
0.
0.
0.292623
0.
0.
In[]:=
u.s//MatrixForm
Out[]//MatrixForm=
1.14227
0.168946
0.418101
-0.230784
-1.56038
0.0618385

1.1.3 Karhunen-Loeve Decomposition

In[]:=
KL=KarhunenLoeveDecomposition[Transpose[Xstd],StandardizedTrue][[1]]//Transpose;MatrixForm[KL]
Out[]//MatrixForm=
1.14227
0.168946
0.418101
-0.230784
-1.56038
0.0618385
In[]:=
Join[z,First[z]]
Out[]=
{{1.14227,0.168946},{0.418101,-0.230784},{-1.56038,0.0618385},1.14227,0.168946}
In[]:=
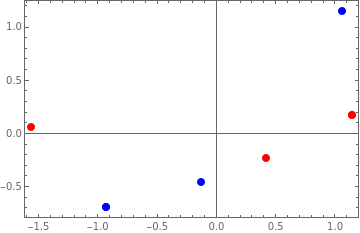
p0=Show[{ListPlot[Join[z,{First[z]}],PlotRangeAll,PlotStyle{PointSizeLarge,Red},AspectRatio0.65],ListPlot[Join[Xstd,{First[Xstd]}],PlotRangeAll,PlotStyle{PointSizeLarge,Blue},AspectRatio0.65]},PlotRangeAll,FrameTrue]​​
Out[]=

1.1.4 PCA and Total Least Square

In[]:=
EigenvectorsX=Transpose[{Transpose[Eigenvectors[S]][[2]],{0,0}}]
Out[]=
{{-0.707107,0},{-0.707107,0}}
In[]:=
XstdX=z.PseudoInverse[EigenvectorsX]
Out[]=
{{-0.80771,-0.80771},{-0.295642,-0.295642},{1.10335,1.10335}}
In[]:=
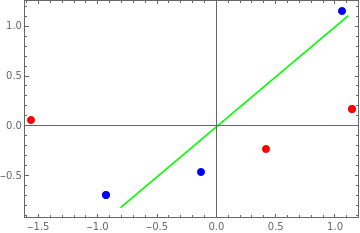
p1=Show[{p0,ListPlot[XstdX,JoinedTrue,PlotStyleGreen]}]
Out[]=
In[]:=
{x,y}=Transpose[Xstd];
In[]:=
obj=Apply[Plus,Table[
2
Δx
i
+
2
(y[[i]]-α(x[[i]]-
Δx
i
)-β)
,{i,1,n}]];

1.1.5 Image Compression

1.1.6 Color Image Compression

1.1.7 Image Compression in Python

Test
〉
In[]:=
5+6
Source
https://plot.ly/ipython-notebooks/principal-component-analysis/
http://dilloncamp.com/projects/pca.html
Setup
〉
In[]:=
from sklearn.decomposition import PCA
from sklearn.preprocessing import normalize
import scipy.io as sio
import matplotlib.image as image
import pandas as pd
import matplotlib.pyplot as plt
Load images
〉
In[]:=
#Image is stored in MATLAB dataset
X = sio.loadmat('D:\\ex7faces.mat')
X = pd.DataFrame(X['X'])
#Normalize data by subtracting mean and scaling
X_norm = normalize(X)
Run PCA
〉
In[]:=
#Set pca to find principal components that explain 99%
#of the variation in the data
pca = PCA(.99)
#Run PCA on normalized image data
lower_dimension_data = pca.fit_transform(X_norm)
#Lower dimension data is 5000x353 instead of 5000x1024
lower_dimension_data.shape
Reconstruct images
〉
In[]:=
#Project lower dimension data onto original features
approximation = pca.inverse_transform(lower_dimension_data)
#Approximation is 5000x1024
approximation.shape
#Reshape approximation and X_norm to 5000x32x32 to display images
approximation = approximation.reshape(-1,32,32)
X_norm = X_norm.reshape(-1,32,32)
Display Images​
The following code displays the original images next to their 99% of variation counterparts. Because of how matplotlib displays images, the pictures may be rotated. If you really want to fix this, you can transpose each row of X_norm and approximation using a for loop.
〉
In[]:=
for i in range(0,X_norm.shape[0]):
X_norm[i,] = X_norm[i,].T
approximation[i,] = approximation[i,].T
fig4, axarr = plt.subplots(3,2,figsize=(8,8))
axarr[0,0].imshow(X_norm[0,],cmap='gray')
axarr[0,0].set_title('Original Image')
axarr[0,0].axis('off')
axarr[0,1].imshow(approximation[0,],cmap='gray')
axarr[0,1].set_title('99% Variation')
axarr[0,1].axis('off')
axarr[1,0].imshow(X_norm[1,],cmap='gray')
axarr[1,0].set_title('Original Image')
axarr[1,0].axis('off')
axarr[1,1].imshow(approximation[1,],cmap='gray')
axarr[1,1].set_title('99% Variation')
axarr[1,1].axis('off')
axarr[2,0].imshow(X_norm[2,],cmap='gray')
axarr[2,0].set_title('Original Image')
axarr[2,0].axis('off')
axarr[2,1].imshow(approximation[2,],cmap='gray')
axarr[2,1].set_title('99% variation')
axarr[2,1].axis('off')
plt.show()