4.4 Robust Regression Models
4.4 Robust Regression Models
4.4.1 Local Regression (loess)
4.4.1 Local Regression (loess)
In[]:=
session=StartExternalSession["Python"]
Out[]=
ExternalSessionObject
Test
In[]:=
5+6
Out[]=
11
In[]:=
wind=Import["E:\\wind.dat"]//Flatten;
In[]:=
ozone=Import["E:\\ozone.dat"]//Flatten;
In[]:=
data=Transpose[{wind,ozone}];
In[]:=
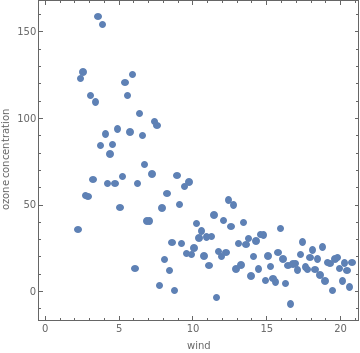
pdata=ListPlot[data,AspectRatio1,PlotRangeAll,AxesOrigin{0,0},PlotStylePointSize[0.02],FrameTrue,FrameLabel{"wind","ozone concentration"}]
Out[]=
In[]:=
T=Compile[{u},If[Abs[u]<1,(1-Abs[u]^3)^3,0]];ww=Compile{{i,_Integer},{x,_Real},{xx,_Real,1},{q,_Integer}},TAbs[xx〚i〛-x]Sort[Abs[xx-x]]q;
In[]:=
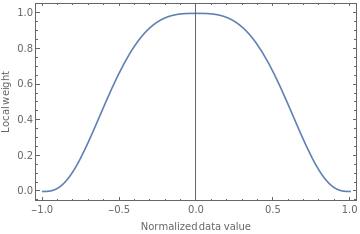
Plot[T[u],{u,-1,1},FrameTrue,FrameLabel{"Normalized data value","Local weight"}]
Out[]=
In[]:=
localRegress[data_,localpols_,α_,λ_]:=Module[{xx,ff,a,b,n,x,q,xwei,y},{xx,ff}=data;a=Min[xx];b=Max[xx];n=Length[xx];x=Range[a,b,(b-a)/(localpols-1)];q=Floor[αn];xwei={#,Table[ww[i,#,xx,q],{i,n}]}&/@x;Interpolation[{#〚1〛,Normal[LinearModelFit[data,y^Range[0,λ],y,Weights#〚2〛+10^-15]]/.y#〚1〛}&/@xwei]]
In[]:=
{fit1,fit2}={localRegress[data,20,0.9,1],localRegress[data,20,0.9,2]};
In[]:=
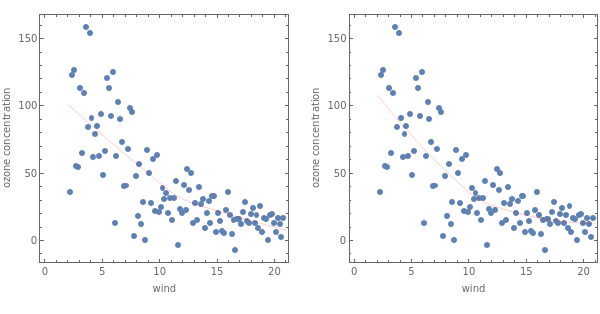
GraphicsGrid[{Map[Show[{pdata,Plot[#[x],{x,2,21},PlotStyle{Thin,Red}]//Quiet}]&,{fit1,fit2}]}]
Out[]=
In[]:=
Export["E:\\wind.mtx",{wind}];
In[]:=
Export["E:\\ozone.mtx",{N[ozone]}];
In[]:=
import numpy as np
import pandas as pd
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
import scipy
import matplotlib.pyplot as plt
import seaborn as sns
In[]:=
import numpy as np
import pandas as pd
import scipy
def loc_eval(x, b):
"""
Evaluate `x` using locally-weighted regression parameters.
Degree of polynomial used in loess is inferred from b. `x`
is assumed to be a scalar.
"""
loc_est = 0
for i in enumerate(b): loc_est+=i[1]*(x**i[0])
return(loc_est)
def loess(xvals, yvals, alpha, poly_degree=1):
"""
Perform locally-weighted regression on xvals & yvals.
Variables used inside `loess` function:
n => number of data points in xvals
m => nbr of LOESS evaluation points
q => number of data points used for each
locally-weighted regression
v => x-value locations for evaluating LOESS
locsDF => contains local regression details for each
location v
evalDF => contains actual LOESS output for each v
X => n-by-(poly_degree+1) design matrix
W => n-by-n diagonal weight matrix for each
local regression
y => yvals
b => local regression coefficient estimates.
b = `(X^T*W*X)^-1*X^T*W*y`. Note that `@`
replaces `np.dot` in recent numpy versions.
local_est => response for local regression
"""
# Sort dataset by xvals.
all_data = sorted(zip(xvals, yvals), key=lambda x: x[0])
xvals, yvals = zip(*all_data)
locsDF = pd.DataFrame(
columns=[
'loc','x','weights','v','y','raw_dists',
'scale_factor','scaled_dists'
])
evalDF = pd.DataFrame(
columns=[
'loc','est','b','v','g'
])
n = len(xvals)
m = n + 1
q = int(np.floor(n * alpha) if alpha <= 1.0 else n)
avg_interval = ((max(xvals)-min(xvals))/len(xvals))
v_lb = max(0,min(xvals)-(.5*avg_interval))
v_ub = (max(xvals)+(.5*avg_interval))
v = enumerate(np.linspace(start=v_lb, stop=v_ub, num=m), start=1)
# Generate design matrix based on poly_degree.
xcols = [np.ones_like(xvals)]
for j in range(1, (poly_degree + 1)):
xcols.append([i ** j for i in xvals])
X = np.vstack(xcols).T
for i in v:
iterpos = i[0]
iterval = i[1]
# Determine q-nearest xvals to iterval.
iterdists = sorted([(j, np.abs(j-iterval)) \
for j in xvals], key=lambda x: x[1])
_, raw_dists = zip(*iterdists)
# Scale local observations by qth-nearest raw_dist.
scale_fact = raw_dists[q-1]
scaled_dists = [(j[0],(j[1]/scale_fact)) for j in iterdists]
weights = [(j[0],((1-np.abs(j[1]**3))**3 \
if j[1]<=1 else 0)) for j in scaled_dists]
# Remove xvals from each tuple:
_, weights = zip(*sorted(weights, key=lambda x: x[0]))
_, raw_dists = zip(*sorted(iterdists, key=lambda x: x[0]))
_, scaled_dists = zip(*sorted(scaled_dists,key=lambda x: x[0]))
iterDF1 = pd.DataFrame({
'loc' :iterpos,
'x' :xvals,
'v' :iterval,
'weights' :weights,
'y' :yvals,
'raw_dists' :raw_dists,
'scale_fact' :scale_fact,
'scaled_dists':scaled_dists
})
locsDF = pd.concat([locsDF, iterDF1])
W = np.diag(weights)
y = yvals
b = np.linalg.inv(X.T @ W @ X) @ (X.T @ W @ y)
local_est = loc_eval(iterval, b)
iterDF2 = pd.DataFrame({
'loc':[iterpos],
'b' :[b],
'v' :[iterval],
'g' :[local_est]
})
evalDF = pd.concat([evalDF, iterDF2])
# Reset indicies for returned DataFrames.
locsDF.reset_index(inplace=True)
locsDF.drop('index', axis=1, inplace=True)
locsDF['est'] = 0; evalDF['est'] = 0
locsDF = locsDF[['loc','est','v','x','y','raw_dists',
'scale_fact','scaled_dists','weights']]
# Reset index for evalDF.
evalDF.reset_index(inplace=True)
evalDF.drop('index', axis=1, inplace=True)
evalDF = evalDF[['loc','est', 'v', 'b', 'g']]
return(locsDF, evalDF)
import pandas as pd
import scipy
def loc_eval(x, b):
"""
Evaluate `x` using locally-weighted regression parameters.
Degree of polynomial used in loess is inferred from b. `x`
is assumed to be a scalar.
"""
loc_est = 0
for i in enumerate(b): loc_est+=i[1]*(x**i[0])
return(loc_est)
def loess(xvals, yvals, alpha, poly_degree=1):
"""
Perform locally-weighted regression on xvals & yvals.
Variables used inside `loess` function:
n => number of data points in xvals
m => nbr of LOESS evaluation points
q => number of data points used for each
locally-weighted regression
v => x-value locations for evaluating LOESS
locsDF => contains local regression details for each
location v
evalDF => contains actual LOESS output for each v
X => n-by-(poly_degree+1) design matrix
W => n-by-n diagonal weight matrix for each
local regression
y => yvals
b => local regression coefficient estimates.
b = `(X^T*W*X)^-1*X^T*W*y`. Note that `@`
replaces `np.dot` in recent numpy versions.
local_est => response for local regression
"""
# Sort dataset by xvals.
all_data = sorted(zip(xvals, yvals), key=lambda x: x[0])
xvals, yvals = zip(*all_data)
locsDF = pd.DataFrame(
columns=[
'loc','x','weights','v','y','raw_dists',
'scale_factor','scaled_dists'
])
evalDF = pd.DataFrame(
columns=[
'loc','est','b','v','g'
])
n = len(xvals)
m = n + 1
q = int(np.floor(n * alpha) if alpha <= 1.0 else n)
avg_interval = ((max(xvals)-min(xvals))/len(xvals))
v_lb = max(0,min(xvals)-(.5*avg_interval))
v_ub = (max(xvals)+(.5*avg_interval))
v = enumerate(np.linspace(start=v_lb, stop=v_ub, num=m), start=1)
# Generate design matrix based on poly_degree.
xcols = [np.ones_like(xvals)]
for j in range(1, (poly_degree + 1)):
xcols.append([i ** j for i in xvals])
X = np.vstack(xcols).T
for i in v:
iterpos = i[0]
iterval = i[1]
# Determine q-nearest xvals to iterval.
iterdists = sorted([(j, np.abs(j-iterval)) \
for j in xvals], key=lambda x: x[1])
_, raw_dists = zip(*iterdists)
# Scale local observations by qth-nearest raw_dist.
scale_fact = raw_dists[q-1]
scaled_dists = [(j[0],(j[1]/scale_fact)) for j in iterdists]
weights = [(j[0],((1-np.abs(j[1]**3))**3 \
if j[1]<=1 else 0)) for j in scaled_dists]
# Remove xvals from each tuple:
_, weights = zip(*sorted(weights, key=lambda x: x[0]))
_, raw_dists = zip(*sorted(iterdists, key=lambda x: x[0]))
_, scaled_dists = zip(*sorted(scaled_dists,key=lambda x: x[0]))
iterDF1 = pd.DataFrame({
'loc' :iterpos,
'x' :xvals,
'v' :iterval,
'weights' :weights,
'y' :yvals,
'raw_dists' :raw_dists,
'scale_fact' :scale_fact,
'scaled_dists':scaled_dists
})
locsDF = pd.concat([locsDF, iterDF1])
W = np.diag(weights)
y = yvals
b = np.linalg.inv(X.T @ W @ X) @ (X.T @ W @ y)
local_est = loc_eval(iterval, b)
iterDF2 = pd.DataFrame({
'loc':[iterpos],
'b' :[b],
'v' :[iterval],
'g' :[local_est]
})
evalDF = pd.concat([evalDF, iterDF2])
# Reset indicies for returned DataFrames.
locsDF.reset_index(inplace=True)
locsDF.drop('index', axis=1, inplace=True)
locsDF['est'] = 0; evalDF['est'] = 0
locsDF = locsDF[['loc','est','v','x','y','raw_dists',
'scale_fact','scaled_dists','weights']]
# Reset index for evalDF.
evalDF.reset_index(inplace=True)
evalDF.drop('index', axis=1, inplace=True)
evalDF = evalDF[['loc','est', 'v', 'b', 'g']]
return(locsDF, evalDF)
In[]:=
import numpy as np
In[]:=
from numpy import array, matrix
In[]:=
from scipy.io import mmread, mmwrite
In[]:=
xv=mmread('E:\\wind.mtx')
In[]:=
xvals=xv[0]
In[]:=
yv=mmread('E:\\ozone.mtx')
In[]:=
yvals=yv[0]
In[]:=
regsDF, evalDF = loess(xvals, yvals, alpha=.9, poly_degree=1)
In[]:=
l_x=evalDF['v'].values
l_x
l_x
Out[]=
NumericArray
In[]:=
Normal[%]
Out[]=
{2.13423,2.30148,2.46873,2.63597,2.80322,2.97046,3.13771,3.30495,3.4722,3.63945,3.80669,3.97394,4.14118,4.30843,4.47568,4.64292,4.81017,4.97741,5.14466,5.3119,5.47915,5.6464,5.81364,5.98089,6.14813,6.31538,6.48263,6.64987,6.81712,6.98436,7.15161,7.31885,7.4861,7.65335,7.82059,7.98784,8.15508,8.32233,8.48958,8.65682,8.82407,8.99131,9.15856,9.3258,9.49305,9.6603,9.82754,9.99479,10.162,10.3293,10.4965,10.6638,10.831,10.9983,11.1655,11.3328,11.5,11.6672,11.8345,12.0017,12.169,12.3362,12.5035,12.6707,12.838,13.0052,13.1725,13.3397,13.5069,13.6742,13.8414,14.0087,14.1759,14.3432,14.5104,14.6777,14.8449,15.0122,15.1794,15.3467,15.5139,15.6811,15.8484,16.0156,16.1829,16.3501,16.5174,16.6846,16.8519,17.0191,17.1864,17.3536,17.5208,17.6881,17.8553,18.0226,18.1898,18.3571,18.5243,18.6916,18.8588,19.0261,19.1933,19.3606,19.5278,19.695,19.8623,20.0295,20.1968,20.364,20.5313,20.6985,20.8658}
In[]:=
u=%;
In[]:=
l_y=evalDF['g'].values
l_y
l_y
Out[]=
NumericArray
Fig.4.4.4 Local regression with polynomial of first degree
In[]:=
regsDF, evalDF = loess(xvals, yvals, alpha=.9, poly_degree=2)
regsDF, evalDF = loess(xvals, yvals, alpha=.9, poly_degree=2)
In[]:=
l_x=evalDF['v'].values
l_x
l_x
In[]:=
l_y=evalDF['g'].values
l_y
l_y
4.4.2 Expectation Maximization
4.4.2 Expectation Maximization
The result of the parameter values
In[]:=
from numpy import array, matrix
from scipy.io import mmread, mmwrite
from numpy import array, matrix
from scipy.io import mmread, mmwrite
In[]:=
caki=mmread('E:\cuki.mtx')
In[]:=
import numpy as np
from sklearn.mixture import GaussianMixture
from sklearn.mixture import GaussianMixture
In[]:=
gmm=GaussianMixture(n_components=2).fit(caki)
In[]:=
labels=gmm.predict(caki)
labels
labels
4.4.3 Maximum Likelihood Estimation
4.4.3 Maximum Likelihood Estimation
In[]:=
from numpy import array, matrix
from scipy.io import mmread, mmwrite
from numpy import array, matrix
from scipy.io import mmread, mmwrite
In[]:=
xcaki=mmread('E:\zcuki.mtx')
ycaki=mmread('E:\ycuki.mtx')
ycaki=mmread('E:\ycuki.mtx')
In[]:=
import numpy as np
from scipy.optimize import minimize
import scipy.stats as stats
from scipy.optimize import minimize
import scipy.stats as stats
In[]:=
def regressLL(params):
a0 = params[0]
a1 = params[1]
a2 = params[2]
sd = params[3]
yPred=a0+ a1*xcaki**0.5+a2*xcaki
logLik = -np.sum( stats.norm.logpdf(ycaki, loc=yPred, scale=sd) )
return(logLik)
a0 = params[0]
a1 = params[1]
a2 = params[2]
sd = params[3]
yPred=a0+ a1*xcaki**0.5+a2*xcaki
logLik = -np.sum( stats.norm.logpdf(ycaki, loc=yPred, scale=sd) )
return(logLik)
In[]:=
initParams=np.array([1,2,0,1])
In[]:=
results = minimize(regressLL, initParams, method='nelder-mead')
In[]:=
results.x
4.4.4 RANSAC for Linear Models
4.4.4 RANSAC for Linear Models
In[]:=
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/rasbt/'
'python-machine-learning-book-2nd-edition'
'/master/code/ch10/housing.data.txt',
header=None,
sep='\s+')
df.columns=['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT','MEDV']
X = df[['LSTAT']].values
y = df['MEDV'].values
df = pd.read_csv('https://raw.githubusercontent.com/rasbt/'
'python-machine-learning-book-2nd-edition'
'/master/code/ch10/housing.data.txt',
header=None,
sep='\s+')
df.columns=['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT','MEDV']
X = df[['LSTAT']].values
y = df['MEDV'].values
In[]:=
np.savetxt('E:\\daTaX.txt',X,fmt='%.5e')
In[]:=
np.savetxt('E:\\daTay.txt',y,fmt='%.5e')
In[]:=
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import RANSACRegressor
from sklearn.linear_model import RANSACRegressor
In[]:=
ransac=RANSACRegressor(LinearRegression(),max_trials=100,min_samples=50,loss='absolute_loss',residual_threshold=5.0,random_state=0).fit(X,y)
In[]:=
inlier_mask=ransac.inlier_mask_
In[]:=
np.savetxt('E:\\maskedX.txt',X[inlier_mask],fmt='%.5e')
In[]:=
np.savetxt('E:\\maskedy.txt',y[inlier_mask],fmt='%.5e')