Graph states (also known as cluster states) are a specific class of multi-qubit entangled states that are defined based on graphs. Each vertex of the graph corresponds to a qubit, and the edges represent entanglement between the qubits. Graph states are foundational to the one-way quantum computing model (measurement-based quantum computing), where quantum computation is achieved through a sequence of adaptive measurements on an initial graph state. Using
QuantumCircuitOperator[{"Graph",
Graph
[…]}]
, one can create a circuit that generates the corresponding quantum graph state.
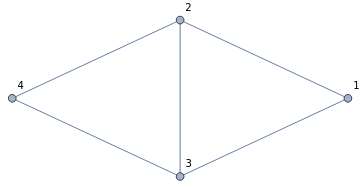
Generate a random graph with 4 vertexes and 5 edges:
In[62]:=
g=RandomGraph[{4,5},VertexLabels->Automatic]
Out[62]=
Create the corresponding quantum circuit:
In[63]:=
qc=QuantumCircuitOperator[{"Graph",g}]
Out[63]=
QuantumCircuitOperator
​

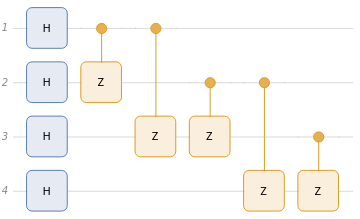
Circuit diagram:
In[64]:=
qc["Diagram"]
Out[64]=
Show that the circuit acting on a register state creates the expected quantum cluster/graph state:
In[65]:=
ψf=qc[]
Out[65]=
QuantumState
Pure state
Qudits: 4
Type: Vector
Dimension: 16
Picture: Schrödinger
​

In[66]:=
ψf==QuantumState[{"Graph",g}]
Out[66]=
True
Show qubits connected via an edge are entangled:
In[73]:=
QuantumEntangledQ[ψf,{#1,#}]&@@@EdgeList[g]
Out[73]=
{True,True,True,True,True}
Given a vertex of the graph, find list of vertices adjacent to it:
In[67]:=
verAdj=Transpose[Through[{VertexList,AdjacencyList}[g]]]
Out[67]=
{{1,{2,3}},{2,{1,3,4}},{3,{1,2,4}},{4,{2,3}}}
Now let's find stabilizers, which simply are are a set of operators that represents the symmetries of a quantum state. Given above the list of vertices and their adjacencies, one can find corresponding stabilizer, which can be obtain by Pauli-X on vertex and Pauli-Z on adjacencies.
Return stabilizer list:
In[68]:=
stabilizers=QuantumOperator[{"X"->#1,"Z"->#2}]&@@@verAdj
Out[68]=
QuantumOperator
Picture: Schrödinger
Arity: 3
Dimension: 8→8
Qudits: 3→3
,QuantumOperator
Picture: Schrödinger
Arity: 4
Dimension: 16→16
Qudits: 4→4
,QuantumOperator
Picture: Schrödinger
Arity: 4
Dimension: 16→16
Qudits: 4→4
,QuantumOperator
Picture: Schrödinger
Arity: 3
Dimension: 8→8
Qudits: 3→3

Apply above list of stabilizers and show that the result (graph state being transformed by a stabilizer) is still the same as the original state (that is why it is called stabilizer):
In[69]:=
Thread[Through[stabilizers[ψf]]==ψf]
Out[69]=
{True,True,True,True}