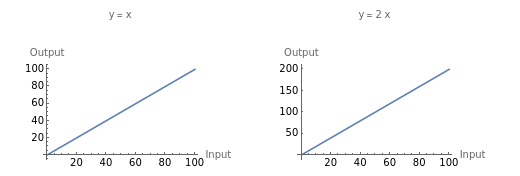
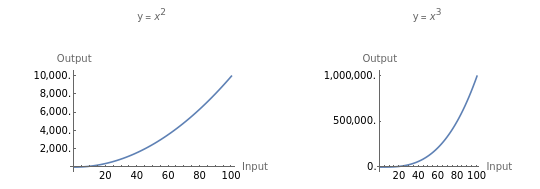
In what follows we will use the default values shown above of 900 initial cases, a cycle length in days of 8.3 and a target value of 45,000 cases where the number of days to reach the target is 46.844. This is a stylized illustration with arbitrary limits intended to demonstrate how the complexity of exponential relationships among many variables may be simplified to answer a specific question.
Below, in blue, is a plot of the equation which produces a result (the vertical axis showing the number of days to reach the target) from the two inputs, cycle length and initial cases. The plot is curved because the equation which produces it involves exponents. On top, in goldenrod, is a flat plot of the 45,000 case target, with a static value on the vertical axis of 46.844 days. The static plot “slices” the blue plot along a red line which represents all the combinations of initial cases and cycle length which may be combined to produce 46.844 days.
What, you may ask, does this do for us?