What is “Fair”? - Part I
[Note: some graphics below are interactive so browser speed will be important]
The essence, indeed the very beginning, of any scientific argument is definition. Axioms and first principles rest on defining what a thing means. Imagine if the process were reversed. We start by announcing The Truth and then define what “Truth” means. For instance, we say that a bowling ball thrown out the window on the tenth floor of a building will float toward the sky. We then define “floating to the sky” as the ball crashing to the ground. I suppose...
The experiment
The experiment
What follows is ambitious. In one light it could be just a variation of, and equally silly as, the bowling ball example. A different, and more charitable, perspective might be that what appears below sheds light on the way our society is organized.
We will assume that anchoring one’s thinking to physical reality has merit. Get rid of the bowling ball. Take a coin and flip it a few times. What you get is the twin reality that (a) it will fall down to the ground; and (b) it will rest with "Heads" facing up about half the time. Somewhat like the bowling ball, a coin is an object you may send airborne and you want to predict what will happen next. The standard definition of a coin includes (a) it is two sided (can't land on its edge) and (b) it is "fair" in that the weight on each side is distributed evenly so that the coin itself is neutral about how it lands, making either side equally (50%) probable. Thus, "fair" is defined as "equi-probable." Every human soul of good intent wants the world and life in general to be "fair." The nagging question that follows us everywhere is: How do we get that outcome?
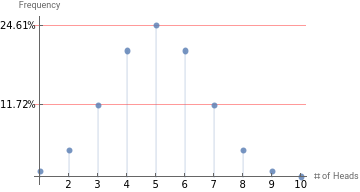
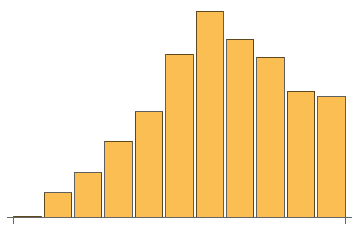
Having now connected physical reality and probability, let's introduce the political economy in which many people on a crowded planet try to live together peacefully. To do that (and to bypass without ignoring some mathematical formalities) we will examine a series of experiments. In each experiment we simultaneously flip ten people into the air and see what happens in each time. Thus, the series of experiments may be seen as repeated trials of the same experiment with ten coins substituted for ten people to minimize the hospitalization. We use the coin as an abstraction but as we go through this it is important to remember it is YOU that is in the air along with nine of your closest friends. We will also arbitrarily assume that landing with “Head” facing up is a good thing. To dramatize and personalize it slightly, assume that coming to rest with “Head” facing up is equivalent to “landing on your feet” just as “tails” is beneath the coin when it is “Head’s up”. Below we run the experiment ten times and, not surprisingly, the result is five heads out of ten most of the time, but not all of the time. The importance of this feature should become clear later, but here is a hint: not all outcomes are equal because not everyone can land on their feet. Below 5 heads occurs just under 25% of the time and either 3 or 7 occur a little less than 12% of the time.
We will assume that anchoring one’s thinking to physical reality has merit. Get rid of the bowling ball. Take a coin and flip it a few times. What you get is the twin reality that (a) it will fall down to the ground; and (b) it will rest with "Heads" facing up about half the time. Somewhat like the bowling ball, a coin is an object you may send airborne and you want to predict what will happen next. The standard definition of a coin includes (a) it is two sided (can't land on its edge) and (b) it is "fair" in that the weight on each side is distributed evenly so that the coin itself is neutral about how it lands, making either side equally (50%) probable. Thus, "fair" is defined as "equi-probable." Every human soul of good intent wants the world and life in general to be "fair." The nagging question that follows us everywhere is: How do we get that outcome?
Having now connected physical reality and probability, let's introduce the political economy in which many people on a crowded planet try to live together peacefully. To do that (and to bypass without ignoring some mathematical formalities) we will examine a series of experiments. In each experiment we simultaneously flip ten people into the air and see what happens in each time. Thus, the series of experiments may be seen as repeated trials of the same experiment with ten coins substituted for ten people to minimize the hospitalization. We use the coin as an abstraction but as we go through this it is important to remember it is YOU that is in the air along with nine of your closest friends. We will also arbitrarily assume that landing with “Head” facing up is a good thing. To dramatize and personalize it slightly, assume that coming to rest with “Head” facing up is equivalent to “landing on your feet” just as “tails” is beneath the coin when it is “Head’s up”. Below we run the experiment ten times and, not surprisingly, the result is five heads out of ten most of the time, but not all of the time. The importance of this feature should become clear later, but here is a hint: not all outcomes are equal because not everyone can land on their feet. Below 5 heads occurs just under 25% of the time and either 3 or 7 occur a little less than 12% of the time.
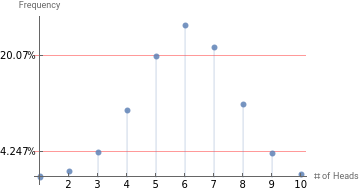
Can we redefine “fair”? Of course we can. It is just a simple matter of weighting the coin. Suppose we decide that “fair” means that for most experiments of ten simultaneous coin flips we get six heads. No problem, we add some weight in just the right place and below we see the outcome. If you were previously in the group landing on your feet five times most often, that outcome now occurs less frequently. It is even less if you were in the group previously enjoying three heads in every toss of ten.
Imagine that each set of ten people are “groups” and each group competes for resources with an uncertain outcome in each competition (flip) of Nature’s coin. It is easy to see how the group favored with the most times landing on their feet would become the target of envy for those less fortunate groups. (Enter politics.)
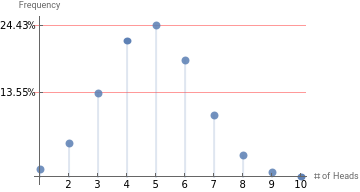
Since our coin flip is “win” or “lose” and therefore a zero sum game (to give to one means take from another), we can simplify to only look at one probability, p. Since all probabilities about a particular event MUST add up to one, the probability of the only remaining outcome must be 1-p (a 60% probability of heads MUST mean a 40% probability of tails). Below you can put your thumb on probability’s scale by moving the slider and choosing the probability you most desire, a choice that will influence the outcome for either your favored group or a group you wish to punish. (Now would be a good time to start thinking about to whom you might give money to accomplish this for you.)
Since our coin flip is “win” or “lose” and therefore a zero sum game (to give to one means take from another), we can simplify to only look at one probability, p. Since all probabilities about a particular event MUST add up to one, the probability of the only remaining outcome must be 1-p (a 60% probability of heads MUST mean a 40% probability of tails). Below you can put your thumb on probability’s scale by moving the slider and choosing the probability you most desire, a choice that will influence the outcome for either your favored group or a group you wish to punish. (Now would be a good time to start thinking about to whom you might give money to accomplish this for you.)
The reality of life
The reality of life
We now make an important assumption, one that is entirely reasonable and universally true: There is NO certainty. There is randomness in any system, therefore in all of life. Hence, it is impossible to remove all risk from life. A corollary to this rule is that anyone who claims to keep you free from risk is, at best, overstating.
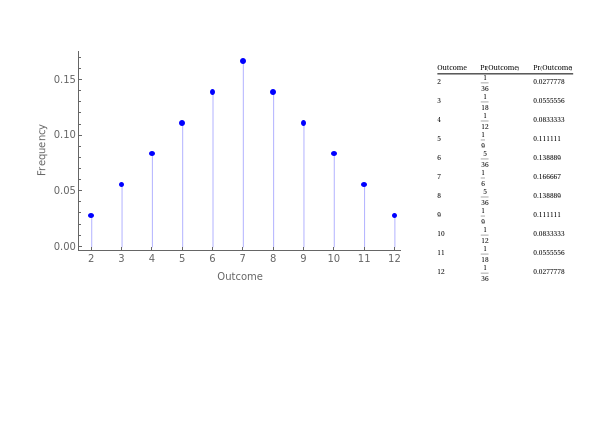
Binary (win-lose, yes-no, one-zero, black-white) examples are easy to model. However, life is more complex. Many situations offer you more options and therefore more outcomes. Dice were invented to handle that. For dice, “fair” is defined as a six sided object (cube), uniform size and shape of all sides and its overall weight distributed evenly throughout. We complicate it by each side having a different number of “pips” providing different “scores” associated with each side landing face up. Below you see the probability of each outcome resulting from throwing a pair of dice. You are now (approximately) playing craps.
Binary (win-lose, yes-no, one-zero, black-white) examples are easy to model. However, life is more complex. Many situations offer you more options and therefore more outcomes. Dice were invented to handle that. For dice, “fair” is defined as a six sided object (cube), uniform size and shape of all sides and its overall weight distributed evenly throughout. We complicate it by each side having a different number of “pips” providing different “scores” associated with each side landing face up. Below you see the probability of each outcome resulting from throwing a pair of dice. You are now (approximately) playing craps.
The most familiar way to create “loaded” dice is to add weight to one side. This method of rigging the game is popular if one wants to cheat at craps because the dice look the same if not examined closely. We are not interested in subterfuge here. To illustrate the concept of “unfair” we will use another method to engineer dice for different outcomes. We will change the taper along four sides such that one end is larger than the other. (There are several assumptions that make what follows work which are described at this link.) This makes the dice into a geometric shape known as a “frustum,” just the sort of word you will want to work into conversation at a cocktail party.
At this stage we could humanize the outcome by imagining you are glued to one side or another and your fate rests on whether you land on the die or the die lands on you. Hopefully, the abstraction is not too great, and you just view life as based on probabilities. True or False: The sum of the choices you make multiplied by their probabilities represent where you end up in life? Throwing dice, indeed throwing a large number of them (ever been married?) at one time repeatedly is a bit scary but a pretty accurate metaphor for life. Indeed, computer simulations have been used for a long time to model life. A particularly sterile one of these may be explored at this link.
Below you can modify the taper and the number of rolls to produce probabilities for various outcomes.
At this stage we could humanize the outcome by imagining you are glued to one side or another and your fate rests on whether you land on the die or the die lands on you. Hopefully, the abstraction is not too great, and you just view life as based on probabilities. True or False: The sum of the choices you make multiplied by their probabilities represent where you end up in life? Throwing dice, indeed throwing a large number of them (ever been married?) at one time repeatedly is a bit scary but a pretty accurate metaphor for life. Indeed, computer simulations have been used for a long time to model life. A particularly sterile one of these may be explored at this link.
Below you can modify the taper and the number of rolls to produce probabilities for various outcomes.
Good vs. Evil
Good vs. Evil
Earlier I urged the reader to keep in mind that all outcomes are not equal. We will now generalize our coin and dice metaphors to consider that. Doing so will require taking a few things on faith but will save you from a calculus refresher. Either way, please accept that there is a mechanism which describes tradeoffs we face quite nicely. That mechanism is known as a parametric plot of a parabola.
Suppose that we go through life making choices. Some are good, some are bad. We measure those choices by the outcome we get, either good things or bad things. Suppose further that we combine those choices in myriad ways to achieve a total, if complex, outcome we call “Life”. We do our best to “optimize” by choosing the right amounts and combinations of good and bad, when we know the difference.
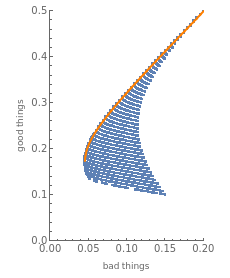
Clearly, we wish to choose only that which delivers good things but fate (probability) intervenes so what Life hands us is a mixed bag. Often we make decisions about what we choose based on a trade-off between payoff and the probability of that payoff. We can get a lower paying job with high security or we can be self-employed with, at the extremes, the possibility of higher income or poverty. Each of us “blends” those choices to form what may be considered a “portfolio” of choices which represents our life. A very famous insight (Markowitz, 1952) described this eloquently for investing. It holds that there is an “efficient frontier” that places decisions properly optimized to balance risk and return along the orange curve trending toward the southwest corner of the plot you see below. Behind that curve are blue dots, each representing a sub-optimal, inefficient choice. Along that curve is a continuum of efficient choices, each representing a different preference for either a risky, more lavish life northeast on the curve or a safer more modest life on the southwest end. Your life is one of the dots on the plot below.
Suppose that we go through life making choices. Some are good, some are bad. We measure those choices by the outcome we get, either good things or bad things. Suppose further that we combine those choices in myriad ways to achieve a total, if complex, outcome we call “Life”. We do our best to “optimize” by choosing the right amounts and combinations of good and bad, when we know the difference.
Clearly, we wish to choose only that which delivers good things but fate (probability) intervenes so what Life hands us is a mixed bag. Often we make decisions about what we choose based on a trade-off between payoff and the probability of that payoff. We can get a lower paying job with high security or we can be self-employed with, at the extremes, the possibility of higher income or poverty. Each of us “blends” those choices to form what may be considered a “portfolio” of choices which represents our life. A very famous insight (Markowitz, 1952) described this eloquently for investing. It holds that there is an “efficient frontier” that places decisions properly optimized to balance risk and return along the orange curve trending toward the southwest corner of the plot you see below. Behind that curve are blue dots, each representing a sub-optimal, inefficient choice. Along that curve is a continuum of efficient choices, each representing a different preference for either a risky, more lavish life northeast on the curve or a safer more modest life on the southwest end. Your life is one of the dots on the plot below.
Who cares?
Who cares?
How does all of this relate? If we agree that life and the world involve complex, partially random, choices rendering a very large number of outcomes (about 7.5 billion at the moment) called people, and if we agree that probability governs those choices and outcomes, we need to establish a RULE about who shall decide. Will it be the individual or the group? We have evidence of what happens under the different conditions. At the extremes, respectively, we have the United States in the early 19th century and Venezuela today.
In the middle we find the USA today or perhaps Sweden. Britain just went through political turmoil over too much of the group in Brussels deciding for them. Small, localized, rebellions are taking place today (April, 2021) over groupthink controlling the choices and movement of the population during a flu virus outbreak.
In the middle we find the USA today or perhaps Sweden. Britain just went through political turmoil over too much of the group in Brussels deciding for them. Small, localized, rebellions are taking place today (April, 2021) over groupthink controlling the choices and movement of the population during a flu virus outbreak.
Measurement
Measurement
Now, here is the punchline: Every one of the choices made by billions of humans either required or actually benefited from measurement. Those who prosper are those who can measure the difference between choices. Sometimes the choice resists measurement. Some measurement involves different choices over time. Sometimes choice measurement is dynamic or operating on moving targets or interdependent choices. Often the measurement is non-linear, perhaps requiring approximation. No one said making choices is easy. But the most important part, the reason any of those measurements or approximations are even close to accurate, is that those measurements are made by the person most affected, the one who must make the choice and live with the consequences.
The last graphic was a static representation, a snapshot of one set of choices at a particular time. In real life the graphic is a representation of the sort of choice matrix everyone on the planet faces every second of every day. Watching the shape of that graphic change in real time as the decision-making heart of society pulses is to grasp the true meaning of the words "all outcomes are not equal." Contemplate the impossibility of a central authority “optimizing” by simultaneously making all those calculations for billions of people.
The last graphic was a static representation, a snapshot of one set of choices at a particular time. In real life the graphic is a representation of the sort of choice matrix everyone on the planet faces every second of every day. Watching the shape of that graphic change in real time as the decision-making heart of society pulses is to grasp the true meaning of the words "all outcomes are not equal." Contemplate the impossibility of a central authority “optimizing” by simultaneously making all those calculations for billions of people.
It is the rich diversity of outcomes, managed for better or worse, by the individuals most affected - themselves - which make our world vibrant, prosperous and interesting. The alternative is management by committee deciding what is “fair.” This results in a new definition of “fair” by people who think they can teach bowling balls to fly.
What “fair” is not
What “fair” is not
Enough for now. We have not yet discovered what “fair” is. We have only discovered what it is not for the individual. We have much work to do. Suppose, unlike coins, people are connected to each other. Is there a “fair” for the group? How is that achieved? Are there circumstances when a clean definition of “fair” is irrelevant? Who gets to decide? Are there conditions when measurement is never required? If some group wants “fair” for itself or some other favored group, how much is that group willing to pay to achieve that end? Is it moral to form a political party to elect people empowered to take an excess of “fair” from one person and give that excess to another? If so, how long can that Robin Hood operation survive?
Heady questions, all... [to be continued]
Heady questions, all... [to be continued]