Tutorial super rápido do Mathematica (que também serve para o Wolfram)
MA311 - Prof. Ricardo M. Martins
O comando abaixo resolve equações. Observe que é preciso usar == (dois sinais de igual) para o Mathematica entender que se trata de uma equação, se usar só um sinal de igual ele vai entender que você está atribuindo valor).
​Muito importante: no Mathematica, para executar uma linha, você precisa apertar shift+enter e não só enter.
Resolvendoequações
In[]:=
Solve[x^2+x-10,x]
Out[]=
x
1
2
(-1-
5
),x
1
2
(-1+
5
)
Quando usamos um só sinal de igual acontece isto:
In[]:=
a=3
Out[]=
3
Agora a variável “a” tem o valor de 3, e você pode fazer contas com ela:
In[]:=
a+2
Out[]=
5
Podemos também resolver equações de forma numérica (usando técnicas que você aprenderá no curso de Cálculo Numérico):
In[]:=
NSolve[x^3-9==0,x]
Out[]=
{{x-1.04004-1.80141},{x-1.04004+1.80141},{x2.08008}}
Pegando só as soluções reais:
In[]:=
NSolve[x^3-9==0,x,Reals]
Out[]=
{{x2.08008}}
Podemos resolver sistemas de equações. Abaixo fazemos um exemplo “analítico” e outro numérico.
In[]:=
Solve[{x+y==2,x-y==8},{x,y}]
Out[]=
{{x5,y-3}}
In[]:=
NSolve[{x^3+2*y==2,x-x*y+y^2==8},{x,y}]
Out[]=
{{x-0.845403-1.90706,y-3.30985-1.4234},{x-0.845403+1.90706,y-3.30985+1.4234},{x0.672622-1.45102,y2.97212-0.54283},{x0.672622+1.45102,y2.97212+0.54283},{x-1.42264,y2.43965},{x1.7682,y-1.76419}}
Só as soluções reais :
In[]:=
NSolve[{x^3+2*y==2,x-x*y+y^2==8},{x,y},Reals]
Out[]=
{{x-1.42264,y2.43965},{x1.7682,y-1.76419}}
​
Plotando gráficos
Para plotar gráficos, o Mathematica tem uma série de comandos. O mais simples deles é o Plot, ou Plot3D, conforme o gráfico seja em R2 ou R3.
In[]:=
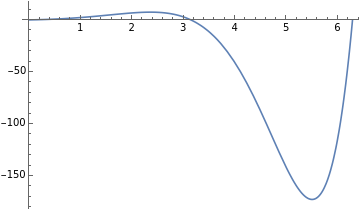
Plot[Exp[x]*Sin[x],{x,0,2*Pi}]
Out[]=
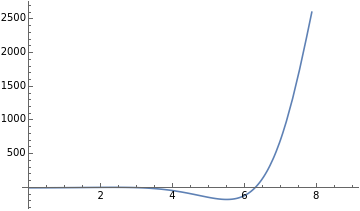
Em alguns gráficos, o eixo y fica “grande” demais, então podemos limitar os eixos. Este é um comando muito útil.
In[]:=
Plot[Exp[x]*Sin[x],{x,0,9}]
Out[]=
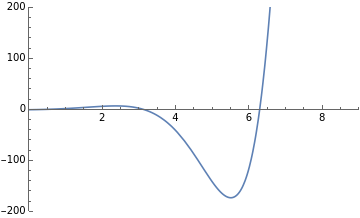
In[]:=
Plot[Exp[x]*Sin[x],{x,0,9},PlotRange{{0,9},{-200,200}}]
Out[]=
Gráficos em 3D são feitos com o comando abaixo. Note que no caso de funções z=f(x,y), você só coloca f(x,y). Precisa também indicar o intervalo de x e de y. No caso abaixo, o domínio é um retângulo.
In[]:=
Plot3D[x^2+2*y^2*Cos[x],{x,-1,1},{y,-2,3}]
Out[]=
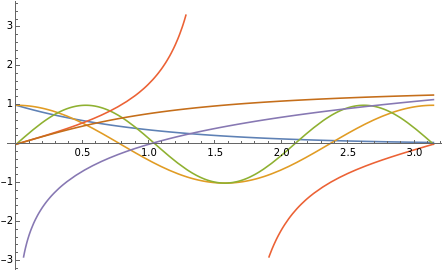
Abaixo vamos plotar várias funções em um mesmo sistema de eixos. Para isto, é só usar a notação de conjunto dentro do Plot. As funções mais “comuns” tem notação bem natural, com a ressalva de que a primeira letra é maiúscula e sempre em inglês. Quando plotamos vários gráficos, o uso de legendas é muito útil, e também está no comando abaixo.
In[]:=
Plot[{Exp[-t],Cos[2t],Sin[3t],Tan[t],Log[t],ArcTan[t]},{t,0,Pi},PlotLegendsLineLegend["Expressions"]]
Out[]=
exp(-t)
cos(2t)
sin(3t)
tan(t)
log(t)
-1
tan
(t)

Derivadas e integrais

O comando D[f,x] calcula a derivada de f com respeito a x. O comando Integrate[g,x] calcula a integral de g com respeito a x.
In[]:=
D[t*Sin[t],t]
Out[]=
tCos[t]+Sin[t]
A derivada de segunda ordem pode ser calculada com D[f,t,t], a de terceira ordem com D[f,t,t,t] e assim em diante.
In[]:=
D[Exp[t]*Cos[t],t,t,t]
Out[]=
-2
t

Cos[t]-2
t

Sin[t]
Para integrarmos, também é simples. Tanto se a integral for definida como se ela for indefinida.
In[]:=
Integrate[x^5,x]
Out[]=
6
x
6
Para a integral definida, por exemplo de 0 a 2, é só colocar {t,0,2} no comando.
In[]:=
Integrate[t^3,{t,0,2}]
Out[]=
4
Equações diferenciais!
Especificamente para equações diferenciais, o Mathematica tem duas formas de trabalhar: analiticamente e numericamente. O comando DSolve resolve (ou tenta resolver) analiticamente equações diferenciais. Já o NDSolve resolve numericamente. Para fazer gráficos, o NDSolve é muitas vezes mais adequado. Observo que o DSolve às vezes usa expressões de funções integrais no meio da resposta, então é preciso cuidado para interpretar os resultados.
Solução geral de uma EDO. Dá para usar normalmente a notação y’[x], observando o uso de [‘s ao invés de (‘s. As constantes vão aparecer com nomes c1, c2, etc.
In[]:=
DSolve[y''[x]+y'[x]Sin[x],y,x]
Out[]=
yFunction{x},

2
+
1
2
(-2
-x


1
-Cos[x]-Sin[x])
Para resolver um PVI, basta adicionar as condições inicia, lembrando de usar a notação de conjunto. O sol1 na linha de baixo é só para dar um nome a esta linha, para usarmos depois.
In[]:=
sol1=DSolve[{y''[x]+y'[x]Sin[x],y[0]==1,y'[0]==2},y,x]
Out[]=
yFunction{x},-
1
2
-x

(5-8
x

+
x

Cos[x]+
x

Sin[x])
Abaixo fazemos o gráfico da solução obtida acima. A parte y[x]/.sol1 faz o seguinte: ela substitui y[x] pelo y[x] obtido no comando anterior, ou seja, pela solucao da equação. O intervalo em que queremos ver a solucao é o [0,30], e no caso do somando DSolve, podemos esticar este intervalo o quanto quisermos.

Soluções numéricas para EDOs

Veja agora o caso abaixo. O Mathematica não consegue resolver esta equação analiticamente.
Teremos que partir para uma solução numérica, com o comando NDSolve. Abaixo resolvemos a equação para t no intervalo [1,3].
Com a solução numérica, temos os valores da função y(t) para todos os valores de t entre 1 e 3. Se quisermos saber y(2), por exemplo, o comando é
Para plotar estes valores, usamos novamente o comando Plot:
Vamos resolver mais uma EDO numericamente. O intervalo de solução é [0,10].
Se formos plotar o gráfico da solução da EDO acima entre 0 e 4*Pi (note que 4*Pi é maior que 12), acontecerá o seguinte:
O gráfico acima está errado. O erro? Nossa solução do NDSolve só é válida entre 0 e 10, que foi o intervalo que pedimos para ele. Então não podemos usar um intervalo maior para ver o gráfico. Podemos corrigir isto resolvendo num intervalo maior, ou então usando o DSolve (quando possível), como fazemos abaixo:
Veja como o gráfico abaixo (correto) é diferente do gráfico acima (errado). Cuidado ao usar softwares!
Vamos obter a solução analítica.
Plotando esta solução, vemos que bate com o resultado numérico quando fizemos da forma certa.
Transformada de Laplace
Abaixo os dois comandos fundamentais para calcular transformadas de Laplace. O t,s no final diz que a entrada é uma função de t e a saída é uma função de s (as variáveis tradicionais).
Agora a transformada inversa:
Sistemas de equações diferenciais
Por último, soluções de sistemas de equações diferenciais, que veremos mais para frente. O único detalhe diferente dos anteriores é que quando temos um sistema, por exemplo envolvendo x’[t] e y’[t], iremos plotar a solução também como uma curva parametrizada.
Encontrada a solução, podemos plotar normalmente como funções “independentes”, x[t] e y[t]:
Ou então podemos plotar como uma curva parametrizada, o que faz mais sentido para sistemas autônomos.
Note que para sistemas não-lineares de equações, raramente o DSolve vai funcionar, e teremos que partir para o NDSolve se quisermos plotar as soluções.
O comando abaixo, tentativa de resolver usando o DSolve, no meu computador, não teve retorno após alguns minutos rodando..
Se usarmos o NDSolve, a solução numérica é calculada.
Podemos plotar as soluções individualmente..
.. ou então podemos plotar como uma curva parametrizada.
Enfim, é isto. O Help do Mathematica é muito bom, e lá vocês conseguirão muitas outras informações. Recomendo também o link abaixo, sobre o DSolve:
https://reference.wolfram.com/language/tutorial/DSolveWorkingWithDSolve.html