You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
Elementary Functions Class Problems
Elementary Functions Class Problems
1
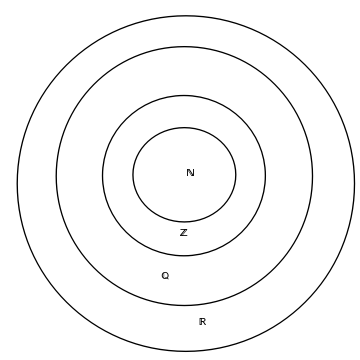
.Given the sets of Natural Numbers, Integers, Rationals and Reals create a diagram that illustrates the containment of these sets.
2
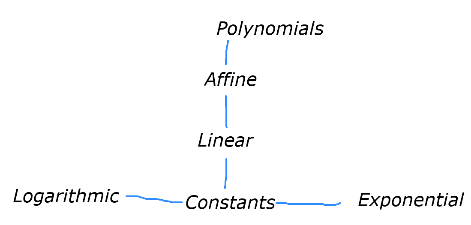
.Consider Constant Functions, Linear Functions, Affine Functions, Polynomials, Exponential Functions, and Logarithmic Functions. Just as with the number sets above, create a diagram of containment that illustrates intersections of these sets of functions.
3
.Consider the function P on the Cartesian plane that is the input being tuples of real numbers that sends the tuple (x,y) to the result x+2y in . Show that this function is linear. That is that for all real numbers it satisfies:
()
2
x,y,,,,,anda
x
1
x
2
y
1
y
2
3
.1
.P(+,+)=P(,)+P(,)
x
1
x
2
y
1
y
2
x
1
y
1
x
2
y
2
3
.1
.1
.P(+,+)=++2(+)=+2++2=P(,)+P(,)
x
1
x
2
y
1
y
2
x
1
x
2
y
1
y
2
x
1
y
1
x
2
y
2
x
1
y
1
x
2
y
2
3
.2
.P(ax,ay)=aP(x,y)
3
.2
.1
.P(ax,ay)=ax+2ay=a(x+2y)=aP(x,y)
4
.Determine the number of Variables, The degree, and the coefficients of the following polynomials.
4
.1
.4
2
x
4
.1
.1
.1 variable, degree 1, [4]
4
.2
.x+y
4
.2
.1
.2 variables, degree 1, [1,1]
4
.3
.2
2
x
3
y
4
.3
.1
.2 variables, degree 5, [2]
4
.4
.2
x
2
y
4
.4
.1
.2 variables, degree 2, [1,2,1]
4
.5
.(x-y)(+xy+)
2
x
2
y
4
.5
.1
.2 variables, degree 3, [1,1]
4
.6
.(x+y)(x-y)+
2
y
4
.6
.1
.1 variable, degree 1, [1]
5
.Find the roots of the following polynomials:
5
.1
.x-1
5
.1
.1
.1
5
.2
.(x-1)(x+2)(x-3)
5
.2
.1
.1,-2,3
5
.3
.2
x
5
.3
.1
.-2,2
5
.4
.(x-3)(+3x+9)
2
x
5
.4
.1
.3
5
.5
.(x+2)(-2x+4)
2
x
5
.5
.1
.-2
6
.Determine if is an exponential function
2*
x
3
6
.1
.It is not let , then but
g(x)=2*
x
3
g(0+0)=2*=2
0+0
3
g(0)*g(0)=4
7
.Determine if 2log(x) is a logarithmic function.
7
.1
.It is. Let . Notice that
f(x)=2log(x)
f(xy)=2log(xy)=2(log(x)+log(y))=2log(x)+2log(y)=f(x)+f(y)
8
.Consider (y) as a binary function on x and y. Determine whether this function is associative or commutative(symmetric).
log
x
8
.1
.The question asks whether ((z))=(y)(z) and if (y)=(x)We can see by examples that this is not the case.
log
x
log
y
log
log
x
log
x
log
y
In[]:=
Log[Log[100,10],10]
Out[]=
-
Log[10]
Log[2]
In[]:=
Log[Log[100,Log[10,10]]]
Out[]=
-∞
In[]:=
Log[10,100]
Out[]=
2
In[]:=
Log[100,10]
Out[]=
1
2
9
.Consider as a binary function on x and y. Determine whether this function is associative or commutative(symmetric).
y
x
9
.1
.The question asks whether = and if =
We can see by examples that this is not the case:
z
()
y
x
()
z
y
x
y
x
x
y
We can see by examples that this is not the case:
In[]:=
(2^3)^4
Out[]=
4096
In[]:=
2^(3^4)
Out[]=
2417851639229258349412352
In[]:=
2^3
Out[]=
8
In[]:=
3^2
Out[]=
9