Elementary Functions.

Special sets of Numbers.

Further in the class we will talk a bit more in detail on general sets and their operations, but to start it will be important to identify a few special number sets and the numbers that comprise them.
For the purpose of this section you may think of a set as a collection of objects, in this case numbers.

The Natural Numbers ()

Denoted by the double-struck-N, the natural numbers are the numbers that we usually use to count. So numbers such as 1, 2, 3, and so on belong on this set.
Depending on the person, textbook, or site that you are interacting with they are going to differ on whether or not the number 0 belongs to the set. For the purpose of this class we will consider that the natural numbers () start with the number 0. So if we were to list them out they would start as 0,1,2,3,4,5,...

The Integer Numbers ()

Denoted by the double-struck-Z (by their name in German [Zal]), the integer numbers are composed by all the natural numbers as above, but also their negatives.
If we were to list out the integers () we would get something like 0,1,-1,2,-2,3,-3,4,-4,...

The Rational Numbers 

Denoted by the double-struck-Q (for quotients) the rational numbers are composed by all numbers that can be expressed as a ratio, or a fraction, of two integers. Namely every number of the form
p
q
where both
p
and
q
are both integers and
q!=0
.
Listing this numbers is possible but quite less intuitive so we will not attempt such task, but we will note some examples.
Note that all integers are also members of the rational numbers. Indeed every integer
n
can be expressed as the fraction
n
1
.
We can also express rational numbers using decimal expansion, such as
1
2
=0.5
. We will note also that those numbers with a repeating decimal expansion will be rational numbers. For example
1
3
=0.3333...
which to avoid ambiguity we will write as
0.
3
(with an overbar on top of the repeating digits) is a rational number. The same occurs with
1
6
=0.1
6
with a repeating 6 at the end of its decimal expansion. The repeating numbers don’t have to be just one, but could be two or more. For example 1.1
75
=
58
33
is another example of a rational number.

The Real Numbers

Denoted by the double-struck-R, the real numbers are the numbers that appear in the number line. The reals () include all the rational numbers as well, but they also include numbers whose decimal expansion is non-repeating. For example, π, the number used to represent the ratio the circumference of a circle and its diameter, is a real number that is not a rational number. The decimal expansion of π begins as 3.14159...
There are some measures for which we will not go too much into detail about, in which we can say that there are more real numbers that are not rational (which we call irrational) rather than rational, which is something that may come up as surprising. But we can construct all types of numbers with non-repeating decimal expansions such as
0.1001000100001000001...
These kinds of procedures can be done with almost any possible combination of numbers imaginable, so having taking this into account should ease the readers mind about these sort of esoteric mathematical facts.
◼
  • https://youtu.be/xnOyr-avXAw

    • Functions

    We will consider mainly functions that go from  to  in this section. We will start with basic functions such as constants, linear, and affine functions, continue with polynomials and finish with a couple transcendental equations .

    Constant Functions

    ◼
  • There is not much we have to say about constant functions on  that we have not already covered before. Constant functions don’t really depend on the argument and it always return the same real number.
    • ◼
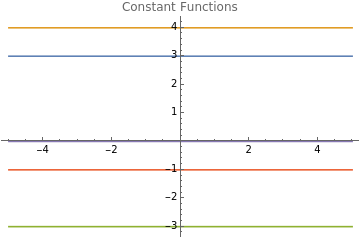
  • All constant functions of one variable over the number line look like a horizontal line
    • Out[]=
    3
    4
    -3
    -1
    0
    ◼
  • All constant functions of two variables over the real plane look like horizontal planes.
    • Out[]=
    5
    -3
    0

    Linear Functions

    ◼
  • A linear function f on  is a function that satisfies
    • ◼
  • f(ax)=af(x)
    , and
    • ◼
  • f(x+y)=f(x)+f(y)
    for all
    a,x,y∈
    • ◼
  • We can summarize the above as
    • ◼
  • f(ax+y)=af(x)+y
    for all
    a,x,y∈
    ,
    • ◼
  • All linear functions on  are of the form
    ​
    f(x)=ax

    for some real number
    a
    .
    • ◼
  • For example
    • ◼
  • f(x)=2x
    • ◼
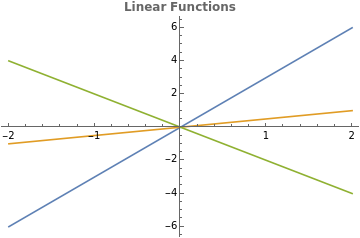
  • All linear functions of one variable look like a line through the origin when they are plotted
    • Out[]=
    3x
    x
    2
    -2x
    ◼
  • All linear functions of two variables look like a plane that goes through the origin.
    • ◼
  • Note how the examples below all intersect at the origin.
    • Out[]=
    2x-4y
    x+y
    6x
    4y
    0
    ◼
  • The sum of linear functions is a linear function.
    • ◼
  • The product of a linear function and a real number is a linear function
    • ◼
  • The composition of linear functions is a linear function
    • ◼
  • https://youtu.be/kBhQB1CcR7w

    • Affine functions

    ◼
  • An affine function on  is a function consisting of a linear function plus a constant.
    • ◼
  • In general they are functions of the form
    ​
    f(x)=ax+b
    for some real numbers
    a
    ,
    b
    .
    • ◼
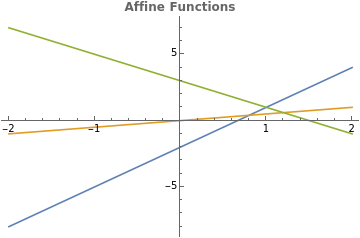
  • All affine functions in one variable over the real numbers look like lines in the Cartesian plane (without necessarily having to cross the origin).
    • Out[]=
    3x-2
    x
    2
    -2x+3
    ◼
  • All affine functions in two variables over the Cartesian plane look like planes in space (without necessarily having to cross the origin).
    • Out[]=
    2x-3y+1
    3x+2
    3-y
    0
    ◼
  • The sum of affine functions is an affine function.
    • ◼
  • The product of an affine function and a real number is an affine function.
    • ◼
  • The composition of affine functions is an affine function.
    • ◼
  • https://youtu.be/kfPCDQPnyf4

    • Polynomials

    Monomials

    Definition of polynomial

    ◼
  • Polynomials are functions that consist of a finite sum of monomials.
    • ◼
  • The following are graphs of different polynomials in one variable

    • Polynomials in several variables

    ◼
  • SImilar to polynomials in one variables, a polynomial in several variables is either a monomial, or a sum of different monomials
    • ◼
  • As we can see polynomials are more flexible than linear and affine functions in terms of the points that can be part of their graph.
    • ◼
  • Nevertheless, polynomials are also harder to work with than linear and affine functions.
    • ◼
  • https://youtu.be/D9qPrsK1lQ8

    • Summation and Product Notation

    Summation Notation

    ◼
  • https://youtu.be/IIkJm8xhzZc

    • Product Notation

    ◼
  • https://youtu.be/lVTVLzcydhI

    • Exponentials

    ◼
  • An exponential is a function that breaks sums into products. In other words:
    f(x + y) = f(x) f(y)
    • ◼
  • This gives us a few properties: Assume that f is an exponential function
    • ◼
  • hi
    • ◼
  • Pf: let x be st f(x) is negative. Then
    • ◼
  • https://youtu.be/BBsvxAjWHfw

    • Logarithms

    ◼
  • This gives us a few properties:

    • Binary Functions

    The most common binary functions on  are addition, subtraction, multiplication and division. There are several others, but we will just focus on these few.

    Properties of General Binary Functions

    ◼
  • There are 2 very common properties of of binary functions on a set.
    • ◼
  • Associativity
    • ◼
  • Symmetry
    • ◼
  • Associativity is the property that lets us do calculations in any order. To be precise, a binary function f is associative if
    • ◼
  • The above may seem partially daunting at first, but let us simplify it using shorthand binary notation.
    • ◼
  • Perhaps it would look even more familiar if we substitute f for an operation symbol such as ⊗
    • ◼
  • Examples of associative functions include addition, and multiplication.
    • ◼
  • For instance (3+4)+7 = 7+7 = 14, and 3+(4+7)= 3+11 = 14.
    • ◼
  • Non examples include division and subtraction
    • ◼
  • For instance (8-4)-2 = 4-2 = 2, while 8-(4-2) = 8 - 2 = 6
    • ◼
  • Written in shorthand notation this is just
    • ◼
  • or with operation symbols
    • ◼
  • As before, addition and multiplication will be examples of symmetric binary functions on 
    • ◼
  • For instance 3×4 = 12 and 4×3 =12
    • ◼
  • Non examples include subtraction and division
    • ◼
  • For instance 4/2 = 2 and 2/4 = 0.5

    • Other properties of Binary Functions

    ◼
  • We say that a binary function f has an identity element if there is an argument  such that
    • ◼
  • For example, 0 is an identity element for addition, and 1 is an identity element for multiplication.
    • ◼
  • Some functions that are not commutative(symmetric) have partial identities or partial inverses. That is, identity elements that work as identities on only one of the inputs.

    • Additional comments

    ◼
  • There are whole textbooks, semester-long or even year-long courses, and even researches whose whole lifework are dedicated to the study of functions that satisfy associativity, having identity elements and having inverses. (Group Theory)
    • ◼
  • There is also a big area of mathematics that studies functions that are associative, have identities, have inverses and are commutative. (Commutative Algebra)
    • ◼
  • Throughout your career you will find and even construct all types of functions and you should think about any kind of properties that they possess to ease your way through working with them.