Relations & Functions

◼
  • When we started to study first order logic and quantification we saw a bit of relations and functions on a set. We actually have a more general notion for these in general. Let us start with Relations

    • Relations

    Intro and Examples

    ◼
  • Formally a relation is a tuple
    (
    A
    1
    ,
    A
    2
    ,...,
    A
    n
    ,R)
    where
    A
    i
    is a set for each
    i∈{1,2,3,...n}
    and
    R⊆
    A
    1
    
    A
    2
    ...
    A
    n
    =
    n
    ∏
    i=1
    A
    i
    . When the sets are clear by context, we usually just denote the relation by R.
    • ◼
  • For the following assume that
    R⊆
    A
    1
    
    A
    2
    ...
    A
    n
    • ◼
  • In general if
    (
    a
    1
    ,...,
    a
    n
    )∈R
    we write
    R(
    a
    1
    ,...,
    a
    n
    ).
    • ◼
  • We call n the arity of R If n =1 we call R a unary relation, if n = 2 we call R a binary relation.
    • ◼
  • Sometimes if R is a binary relation we write
    a
    1
    R
    a
    2
    instead of
    R(
    a
    1
    ,
    a
    2
    )
    . So for example instead of writing
    <=(3,4)
    we write
    3<=4
    • ◼
  • If all
    A
    i
    are equal to a set A then we sometimes say R is a relation over A.
    • ◼
  • Examples:
    • ◼
  • Even = {n∈: ∃k 2k = n}, a unary relation corresponding to the even numbers in 
    • ◼
  • Disc =
    {(x,y)∈
    2
    
    :
    2
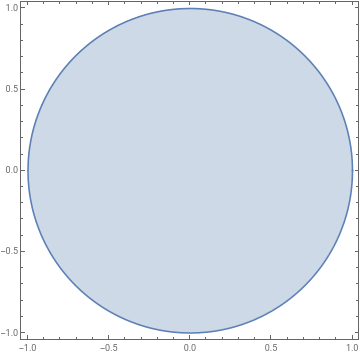
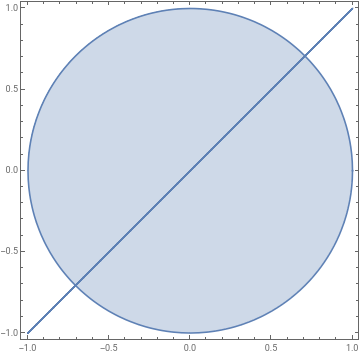
    x
    +
    2
    y
    <=1}
    , the unit disc. It can be represented as
    • Out[]=
    ◼
  • Disc(1,0)
    • ◼
  • Disc(0,0)
    • ◼
  • Disc(0,1)
    • ◼
  • Disc(0.5,0.5)
    • ◼
  • Disc(-1,0)
    • ◼
  • Disc(-0.5,0.5)
    • ◼
  • Disc(0.1,0.1), Disc(0.01,0.01), Disc(0.001,0.001))...
    • ◼
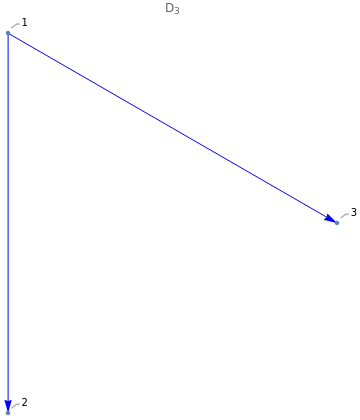
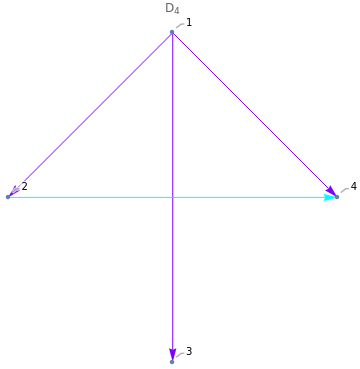
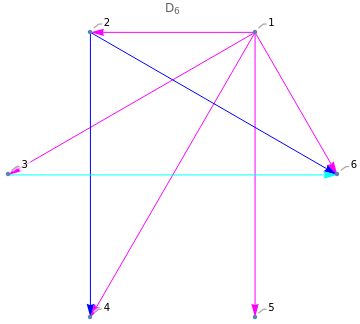
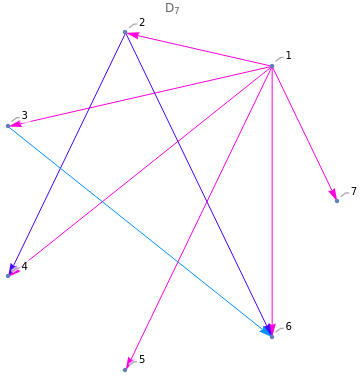
  • D
    n
    =(j,k)∈
    2
    
    :jdivideskandk<=n
    . A representation for D3 through D10 can be seen below, where an edge is drawn between related numbers.Note that j divides k if there is an m such that j*m = k. In here we are just using the definition that j divides k if there is an integer c such that
    cj=k
    .
    • ​
    Out[]=
    ◼
  • D
    3
    (1,3)
    but we do not have
    D
    3
    (3,1)
    ​ In general
    D
    3
    ={(0,0),(1,1),(1,2),(1,3),(2,2),(3,3)}
    • ◼
  • D
    5
    (2,4)
    • ◼
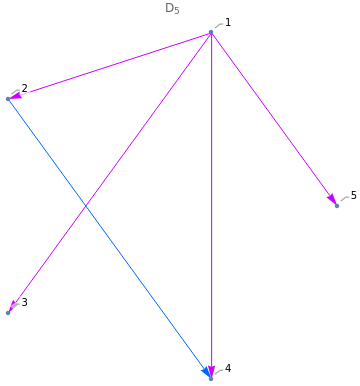
  • Div =
    ⋃
    n∈
    D
    n
    • ◼
  • Sum =
    {(x,y,z)∈
    3
    
    :x+y=z}
    , partially represented below.
    • Out[]=
    ◼
  • Sum(1,1,2)
    • ◼
  • Sum(3,4.53,7.53)
    • ◼
  • NK = {(firstName,
    lastName)∈
    2
    Words
    =WordsWords:firstNamelastNameis
    a
    founderofKibo}
    • ◼
  • Leq =
    {(n,m)∈
    2
    
    :n<=m}
    • ◼
  • Auth = {(x,y)∈ NamesBook Titles: where x is an author of book y}
    • ◼
  • Desc =
    {(x,y)∈
    2
    People
    :xisy'sdescendant}
    • ◼
  • Let X be any set, then Diag =
    {(x,x)∈
    2
    X
    :x=x}
    • ◼
  • Let X be any set Subs = {(A,B)∈(X): A⊆B}
    • ◼
  • Samel = {(x,y) ∈
    2
    Words
    :xandystartwiththesameletter
    }
    • ◼
  • Samel(name,number)
    • ◼
  • Samel(fox,facility)
    • ◼
  • Almost everything can be represented as a relation, and to some extent Mathematics is the study of relations.

    • Parts and properties of a Binary Relation

    ◼
  • Let R⊆AB be a binary relation, then we have the following:
    • ◼
  • The Domain of R
    Dom(R)={a∈A:Thereisb∈Bwith(a,b)∈R}
    • ◼
  • So for example,
    Dom(
    D
    3
    )={0,1,1,1,2,3}={0,1,2,3}
    • ◼
  • Dom(Disc)={x∈:∃y(x^2+y^2)<=1}={x∈:-1<=x<=1}
    • ◼
  • “J.K. Rowling”∈Dom(Auth)
    • ◼
  • The Image of R
    Img(R)={b∈B:Thereisa∈Awith(a,b)∈R}
    • ◼
  • Img(
    D
    3
    )={0,1,2,3}
    • ◼
  • Img(Disc)={x∈:-1<=x<=1}
    • ◼
  • “Harry Potter and the prisoner of Azkaban”
    ∈Img(Auth)
    • ◼
  • If we consider Dom(R)⋃Img(R) = U then we can interpret R as a relation over U.
    • ◼
  • We isolate three important properties of binary relations over a set A.
    • ◼
  • We say that R is reflexive if
    {(a,a)∈
    2
    A
    }⊆R
    • ◼
  • Disc is not reflexive because (1,1) is not in Disc
    • ◼
  • D
    n
    is not reflexive because
    (n+1,n+1)∉
    D
    n
    • ◼
  • Div is reflexive Let n∈. then there is a natural number (in fact n works) where (n,n)
    ∈
    D
    n
    so (n,n)∈Div
    • ◼
  • We say that R is symmetric if
    (a,b)∈R
    implies that
    (b,a)∈R
    • ◼
  • Disc is symmetric: Let x, y ∈ and assume Disc(x,y). Then
    2
    x
    +
    2
    y
    <=1
    . But this means that
    2
    y
    +
    2
    x
    <=1
    . Then by definition Disc(y,x)
    • ◼
  • D
    3
    is not symmetric: since
    D
    3
    (1,3)
    but we do not have
    D
    3
    (3,1)
    • ◼
  • We say that R is transitive if
    (a,b)∈R
    and
    (b,c)∈R
    implies
    (a,c)∈R
    • ◼
  • Disc is not transitive Because Disc(1,0) and Disc(0,1) but we do not have Disc(1,1)
    • ◼
  • Leq in  is transitive Let n,m,k ∈ such that
    n<=m
    and
    m<=k
    . Then we have n
    <=k
    .
    • ◼
  • Let X={1,0} and we take (X,X,R) where R = {(0,1),(1,0),(1,1),(0,0)}
    • ◼
  • Then R is reflexive, symmetric, and transitive
    • ◼
  • Consider the examples above:
    • ◼
  • Disc is symmetric and transitive, but not reflexive
    • ◼
  • D
    n
    for n>0, Leq, and Subs are reflexive and transitive but not symmetric
    • ◼
  • Auth and NK are neither
    • ◼
  • Desc is transitive but not reflexive or symmetric
    • ◼
  • Diag, and Samel are all three.
    • ◼
  • For P. Let a,b,c be words such that aPb, and bPc. So a and b start with the same letter, and b and c start with the same letter. So we can conclude that a and c start with the same letter, so aPc.

    • Closures

    ◼
  • When we are looking at the properties mentioned before, we can always “extend”the relations to satisfy being either reflexive, symmetric, or transitive, or ay combination of them. Given a relation
    R⊆
    2
    A
    we define the following
    • ◼
  • The reflexive closure of R to be the smallest relation
    R
    ref
    (under containment) such that
    R⊆
    R
    ref
    and
    R
    ref
    is reflexive.
    • ◼
  • The symmetric closure of R to be the smallest relation
    R
    sym
    (under containment) such that
    R⊆
    R
    sym
    and
    R
    sym
    is symmetric.
    • ◼
  • The transitive closure of R to be the smallest relation
    R
    trans
    (under containment) such that
    R⊆
    R
    trans
    and
    R
    trans
    is transitive.
    • ◼
  • Notes:
    • ◼
  • Taking the reflexive closure is equivalent to just adding the “diagonal” to our relation
    • ◼
  • Examples:
    • ◼
  • The reflexive closure of the unit disc could be represented as
    • Out[]=

    Equivalence Relations & Partitions

    ◼
  • We say that a relation is an equivalence relation if it satisfies that is is all three, reflexive, symmetric, and transitive.
    • ◼
  • Given a set A, a partition of A is a collection of subsets of A that is pairwise disjoint, and whose union is A.
    • ◼
  • Examples:
    • ◼
  • A = {1,2,3,4,5,6} a partition of A could be = {{1,2}, {3,4}, {5,6}}
    • ◼
  • Consider  a Partition of  could be ={Even, Odd}
    • ◼
  • Partitions and equivalence relations are closely related. In particular one cannot exist without the other. That is, every equivalence relation gives rise to a partition of a set, and every partition of a set gives rise to an equivalence relation.
    • ◼
  • Examples:
    • ◼
  • Examples:
    • ◼
  • We saw that Samel was an equivalence relation. So for each letter we can group the words that start with that letter and so we naturally get a partition of the set of Words.
    ​

    • Functions

    ◼
  • Common notations include:
    • ◼
  • In this course we can mostly consider unary functions F:A⟶B
    • ◼
  • The important condition on a relation to be a function is that every element in the domain is related to a unique element in the codomain.
    • ◼
  • Examples:
    • ◼
  • Sum, Diag, NK are examples of functions

    • Properties of functions

    ◼
  • We say that a function f is injective if f(x)=f(y)  x=y. In other words, if (by the contrapositive) different elements map into different images.
    • ◼
  • We say that a function is bijective if it is both injective and surjective.
    • ◼
  • Examples

    • Extra Notes

    ◼
  • Actually for infinite sets we say that they have the same cardinality if there is a bijection from one set to another.
    • ◼
  • Do the integers and the natural numbers share the same cardinality?
    • ◼
  • f(0)=0, f(1) = -1, f(2)=1, f(3)=-2, f(4)=2, ... note that f is bijective.
    • ◼
  • Fact: The Natural numbers and the Real numbers do not have the same cardinality the proof is a diagonalization argument.

    • Relation Composition

    ◼
  • We can of course then talk about function composition by deriving it from relation composition.