You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
In[]:=
ClearAll
Out[]=
ClearAll
◼
Clear any previous values associated with variables
In[]:=
Clear[a,d,p,p0,n]
In[]:=
Clear[p]
◼
Use the manipulate controls to change the values of your Linear Discrete Dynamical System. p[0] is your initial condition. p[n] is your recursion equation defined as a function.
◼
This control gives you a table of the values for p[n] as you change the value of n. You can also click the + sign and type a specific value into the box to set a specific value.
In[]:=
Manipulate[p[n_]:=a*p[n-1]+d;p[0]=p0;Row[{TableForm[Table[{n,p[n]},{n,0,nmax}],TableHeadings{None,{"n iterations","p[n] output"}}],Framed[Labeled[a,"Multiplication Geometric Parameter a",Top]],Framed[Labeled[d,"Addition Arithmetic Parameter d",Top]],Framed[Labeled[p0,"Inititial Condition p0",Top]],Framed[Labeled[d/(1-a),"Equilibrium Value Pstar=d/(1 - a)",Top]],,Framed[Labeled[N[Solve[d/(1-a)+a^n*(p0-(d/(1-a)))==outvalue,n,Reals]],"Iterations n to Achieve Desired Output",Top]]}],{{a,1},-3,3,1},{{d,0},-10,10,1},{{p0,1},-10,10,1},{{nmax,5},0,10,1},{{outvalue,100},0,1000,100}]
Out[]=
◼
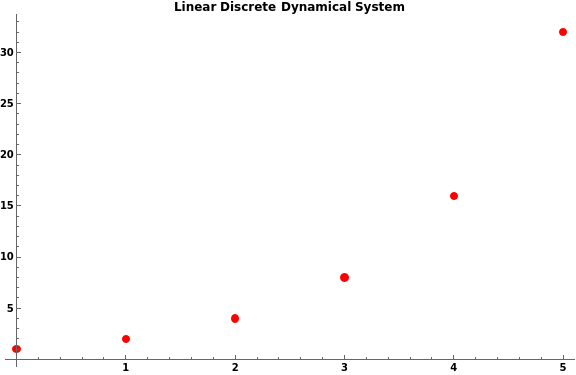
This manipulate controls the plot of your linear discrete dynamical system that you obtain by plotting the time n on the horizontal axis and the output p[n] on the vertical axis.
In[]:=
Manipulate[p[n_]:=a*p[n-1]+d;p[0]=p0;Column[{Show[ListPlot[Table[{n,p[n]},{n,0,nmax}],PlotStylecolor,PlotLabel"Linear Discrete Dynamical System",LabelStyleDirective[Black,Bold]],ImageSizeLarge],Framed[Labeled[a,"Multiplication Geometric Parameter a",Top]],Framed[Labeled[d,"Addition Arithmetic Parameter d",Top]],Framed[Labeled[p0,"Inititial Condition p0",Top]],Framed[Labeled[d/(1-a),"Equilibrium Value Pstar=d/(1 - a)",Top]]}],{{a,1},-3,3,1},{{d,0},-10,10,1},{{p0,1},-10,10,1},{{nmax,5},0,10,1},{{color,Red},{Red,Blue,Green,Brown,Orange,Yellow}}]
Out[]=