You are using a browser not supported by the Wolfram Cloud
Supported browsers include recent versions of Chrome, Edge, Firefox and Safari.
I understand and wish to continue anyway »
WOLFRAM NOTEBOOK
Vector Fields and Path Integrals
Vector Fields and Path Integrals
Vector Fields:
Vector Fields:
In[]:=
F1[x_,y_]={1+2x-y^2,-2x*y};F2[x_,y_]={2x-y,-2x*y};F3[x_,y_]={0.25+y,0.5-x};F4[x_,y_]={-Cos[x-y]-Sin[x-y^2],Cos[x-y]+2y*Sin[x-y^2]};F5[x_,y_]={0.5*y/(x^2+y^2),-0.5*x/(x^2+y^2)};F6[x_,y_]={x,y};
The following command can be used to graph the vector field.
The following command can be used to graph the vector field.
In[]:=
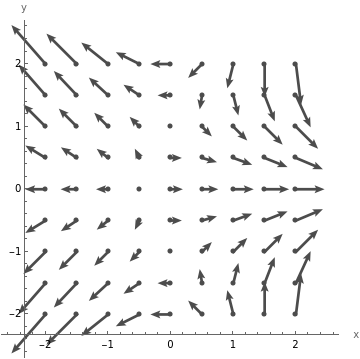
field1=FieldPlotter[F1[x,y],{x,y}]
Out[]=
When the vector field like F5 is not defined at some point, use the following, or you will get an error:
When the vector field like F5 is not defined at some point, use the following, or you will get an error:
In[]:=
field5=FieldPlotter[F5[x,y],{x,y},ValueAtOrigin{0,0}]
Parametric Curves, Part I:
Parametric Curves, Part I:
In[]:=
r1[t_]={t,1-t^2};r2[t_]={t^2-1,t^2*(2-t^2)};r3[t_]={-Cos[t],Sin[t]^2};
The following command can be used to graph the curve. Here the range of t is between -1 and 1.
The following command can be used to graph the curve. Here the range of t is between -1 and 1.
In[]:=
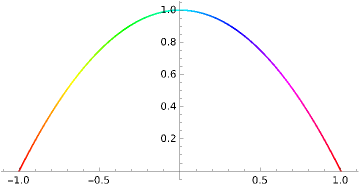
ParametricPlot[r1[t],{t,-1,1},ColorFunctionFunction[{x,y,t},Hue[t]]]
Out[]=
Computing path integrals:
Computing path integrals:
The following command computes the path integral of F1 over the curve described by r1 with t between -1 and 1.
The following command computes the path integral of F1 over the curve described by r1 with t between -1 and 1.
In[]:=
NLineIntegrate[F6[x,y],{x,y},s4[t],{t,-1,1}]
-15
10
-10
10
Out[]=
0
Parametric Curves, Part II:
Parametric Curves, Part II:
In[]:=
s1[t_]={t,1-t^2};s2[t_]={t,.7(t-1)(t+1)(t-.7)};s3[t_]={(t^2)+t-1,Sin[2*Pi*t]};s4[t_]={t+Sin[2*Pi*t]^2,1-Exp[1-t^2]};
In[]:=
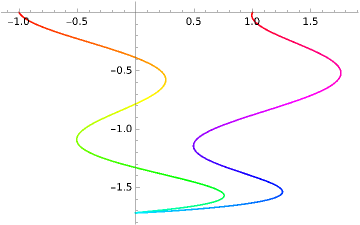
ParametricPlot[s4[t],{t,-1,1},ColorFunctionFunction[{x,y,t},Hue[t]]]
Out[]=
Parametric Curves, Part III:
Parametric Curves, Part III:
s5[t_]={Cos[t]+(1/2)Cos[2*t],(1/2)(Sin[t]-1)+(1/6)Cos[3t]};s6[t_]={.8+Cos[t],0.5*Sin[t]-0.25};s7[t_]={Cos[2t]*Sin[t/2],1+0.5*Sin[2t]*Sin[t/2]};s8[t_]={t(t-2*Pi)/10,1+t(t-2*Pi)(t-1)/30};
The curl of a vector field:
The curl of a vector field:
Curl[F1[x,y],{x,y}]