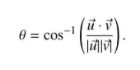◼
Define your vectors in curly brackets. They represent an ordered list of n numbers. Here n=2 for a 2-dimensional vector.
In[]:=
a={1,2}b={3,4}
Out[]=
{1,2}
Out[]=
{3,4}
◼
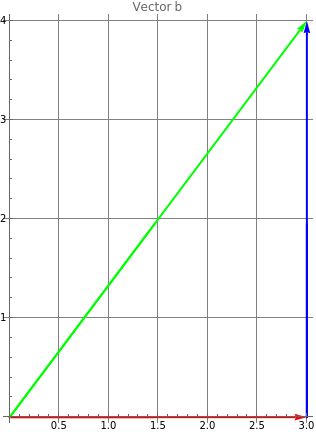
Here is what vector b looks like visually with x component in Red, y component in Blue and the resulting vector in Green.
In[]:=
Graphics[{{Red,Thick,Arrow[{{0,0},{3,0}}]},{Blue,Thickness[Large],Arrow[{{3,0},{3,4}}]},{Green,Thick,Arrow[{{0,0},{3,4}}]}},AxesTrue,GridLinesAutomatic,PlotLabel"Vector b"]
Out[]=
◼
Take the dot product of two vectors
In[]:=
a.b
Out[]=
11
◼
Find the magnitude (length) of the vectors a and b using the Norm command.
In[]:=
magna=Norm[a]
Out[]=
5
In[]:=
magnb=Norm[b]
Out[]=
5
◼
Find the angle between the two vectors a and b defined above by using formula in the text. Inverse Cosine can be accessed using the ArcCos Command in Mathematica. Mathematica defaults to measuring in Radians so you may have to convert.
In[]:=
ArcCos[(a.b)/(magna*magnb)]
Out[]=
ArcCos
11
5
5
◼
To get a numerical approximation using the N command
In[]:=
N[ArcCos[(a.b)/(magna*magnb)]]
Out[]=
0.179853
◼
Convert to Degrees from Radians
In[]:=
N[ArcCos[(a.b)/(magna*magnb)]]*180/Pi
Out[]=
10.3048
◼
Putting all this together in one line here is a command for the angle between the vectors.
In[]:=
N[ArcCos[({1,2}.{3,4})/(Norm[{1,2}]*Norm[{3,4}])]]*180/Pi
Out[]=
10.3048
◼
A unit vector measures 1 unit in length. It has a magnitude of 1 unit. The unit vector created from an existing vector points in the same direction but has a magnitude of 1.
◼
Recall how to calculate the magnitude (length) of vector b.
In[]:=
Norm[b]
Out[]=
5
◼
Turn vector b into the corresponding unit vector that points in the same direction but has a magnitude/length of 1 unit by dividing each element of the original vector by the magnitude of the vector.
◼
You can confirm the length for this 2 dimensional vector by treating each component as a leg side of right triangle and using the pythagorean theorem to calculated the hypotenuse.
In[]:=
unit=b/Norm[b]
Out[]=
,
3
5
4
5
◼
Check the magnitude is 1
In[]:=
Norm[unit]
Out[]=
1
◼
If you treat the horizontal component of your vector as its own vector v1 and the vertical component as its own vector v2 you can solve for the magnitude r or the direction measured as counter clockwise angle from the horizontal x axis by solving for part of the formulas in the following theorem.
◼
◼
The angle of direction of vector b points this direction counter clockwise from the x axis.
In[]:=
N[ArcCos[unit[[1]]]]*180/Pi
Out[]=
53.1301
◼
The opposite complementary angle formed by the triangle follows.
In[]:=
N[ArcCos[unit[[2]]]]*180/Pi
Out[]=
36.8699
◼
You could also input the x component divided by the magnitude of the vector "r" directly in the formula. For vector b from above this value is as follows.
In[]:=
ArcCos[3/5]*180/Pi//N
Out[]=
53.1301
◼
You could use the same formulas given the magnitude and direction to confirm the length of the component vectors
◼
X horizontal component of vector b
In[]:=
Cos[53.1301Degree]*5
Out[]=
3.
◼
Y vertical component of vector b given the magnitude and direction that the vector points.
In[]:=
Sin[53.1301Degree]*5
Out[]=
4.