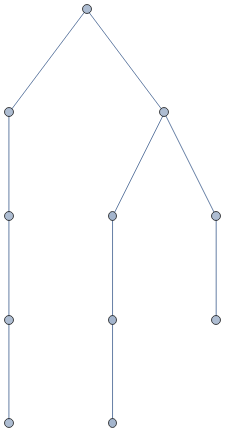
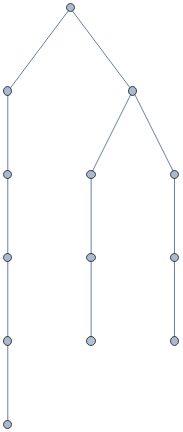
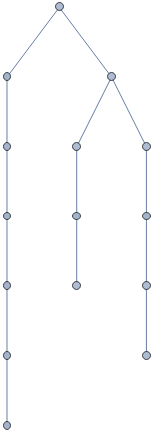
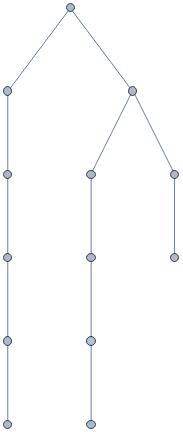
Data structure of state of math: atoms of math [definitions]; relations [math statements]

Evolution: applying laws of inference

In[]:=
ResourceFunction["WolframModel"][{{x,y},{x,z}}->{{x,z},{x,w},{y,w},{z,w}},{{1,2},{2,3},{3,4},{2,4}},4,"StatesList"]
Out[]=
{{{1,2},{2,3},{3,4},{2,4}},{{1,2},{3,4},{2,4},{2,5},{3,5},{4,5}},{{1,2},{4,5},{2,5},{2,6},{4,6},{5,6},{3,5},{3,7},{4,7},{5,7}},{{1,2},{4,7},{2,6},{2,8},{5,8},{6,8},{4,6},{4,9},{5,9},{6,9},{3,7},{3,10},{5,10},{7,10},{5,7},{5,11},{6,11},{7,11}},{{1,2},{4,9},{5,11},{6,11},{2,8},{2,12},{6,12},{8,12},{4,6},{4,13},{7,13},{6,13},{5,9},{5,14},{8,14},{9,14},{6,9},{6,15},{8,15},{9,15},{3,10},{3,16},{7,16},{10,16},{5,7},{5,17},{10,17},{7,17},{7,11},{7,18},{10,18},{11,18}}}
In[]:=
Catenate[ResourceFunction["WolframModel"][{{x,y},{x,z}}->{{x,z},{x,w},{y,w},{z,w}},{{1,2},{2,3},{3,4},{2,4}},4,"StatesList"]]
Out[]=
{{1,2},{2,3},{3,4},{2,4},{1,2},{3,4},{2,4},{2,5},{3,5},{4,5},{1,2},{4,5},{2,5},{2,6},{4,6},{5,6},{3,5},{3,7},{4,7},{5,7},{1,2},{4,7},{2,6},{2,8},{5,8},{6,8},{4,6},{4,9},{5,9},{6,9},{3,7},{3,10},{5,10},{7,10},{5,7},{5,11},{6,11},{7,11},{1,2},{4,9},{5,11},{6,11},{2,8},{2,12},{6,12},{8,12},{4,6},{4,13},{7,13},{6,13},{5,9},{5,14},{8,14},{9,14},{6,9},{6,15},{8,15},{9,15},{3,10},{3,16},{7,16},{10,16},{5,7},{5,17},{10,17},{7,17},{7,11},{7,18},{10,18},{11,18}}
In[]:=
DeleteDuplicates[%]
Out[]=
{{1,2},{2,3},{3,4},{2,4},{2,5},{3,5},{4,5},{2,6},{4,6},{5,6},{3,7},{4,7},{5,7},{2,8},{5,8},{6,8},{4,9},{5,9},{6,9},{3,10},{5,10},{7,10},{5,11},{6,11},{7,11},{2,12},{6,12},{8,12},{4,13},{7,13},{6,13},{5,14},{8,14},{9,14},{6,15},{8,15},{9,15},{3,16},{7,16},{10,16},{5,17},{10,17},{7,17},{7,18},{10,18},{11,18}}
In[]:=
ResourceFunction["MetamathImport"]["$c ( )  wff $.$v p q r s t $.wp $f wff p $.wq $f wff q $.wr $f wff r $.ws $f wff s $.wt $f wff t $.w $a wff ( p  q ) $.w() $p wff ( r  ( s  t ) ) $= wr ws wt w w $.w() $p wff ( ( r  s )  t ) $= wr ws w wt w $."]
Out[]=
Symbols(Constant[(],)Constant[)],Constant[],wffConstant[wff],pVariable[p],qVariable[q],rVariable[r],sVariable[s],tVariable[t],StatementswpHypothesis[wp,{wff,p}],wqHypothesis[wq,{wff,q}],wrHypothesis[wr,{wff,r}],wsHypothesis[ws,{wff,s}],wtHypothesis[wt,{wff,t}],wAxiom[w,{wff,(,p,,q,)},{{},{Hypothesis[wp,{wff,p}],Hypothesis[wq,{wff,q}]},{}}],w()Theorem[w(),{wff,(,r,,(,s,,t,),)},{{},{Hypothesis[wr,{wff,r}],Hypothesis[ws,{wff,s}],Hypothesis[wt,{wff,t}]},{}},{wr,ws,wt,w,w}],w()Theorem[w(),{wff,(,(,r,,s,),,t,)},{{},{Hypothesis[wr,{wff,r}],Hypothesis[ws,{wff,s}],Hypothesis[wt,{wff,t}]},{}},{wr,ws,w,wt,w}]
In[]:=
leanGraph=CloudGet["https://wolfr.am/PL3LfaQ4"];
In[]:=
VertexCount[leanGraph]
Out[]=
35687
In[]:=
Take[VertexList[leanGraph],20]
Out[]=
{group.exists_list_of_mem_closure,lt_add_one,differentiable_at.smul_const,tangent_bundle_proj_open,tactic.ring_exp.mul_pp_pf_overlap,eq_ff_of_not_eq_tt,equiv.of_injective_apply,times_cont_diff.differentiable,nat.elim_zero,simple_graph.adj_iff_exists_edge,int.lt_of_le_sub_one,multiset.card_eq_zero,filter.eventually_bot,pow_eq_zero,valuation.self_le_supp_comap,map_cluster_pt_iff,hyperreal.is_st_st',list.append_inj',set.mem_diff_of_mem,matrix.dot_product_assoc}

Names: 1. of theorems/axioms/hypotheses; 2. of concepts

Also names of types.
Addition facts:
In[]:=
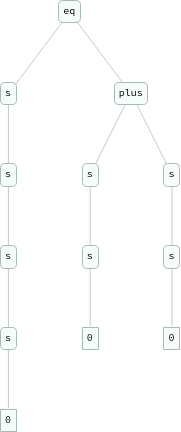
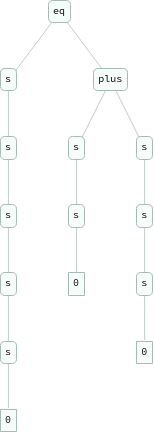
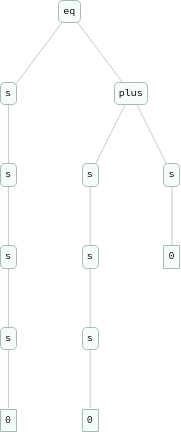
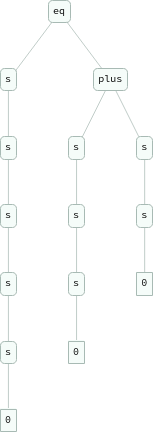
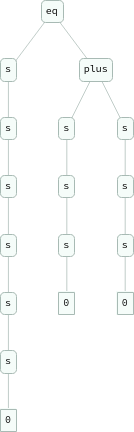
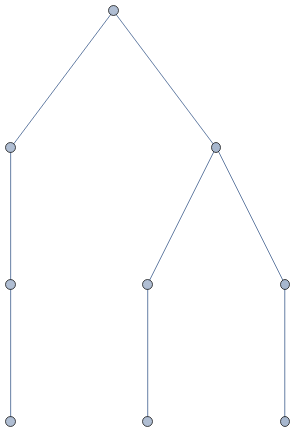
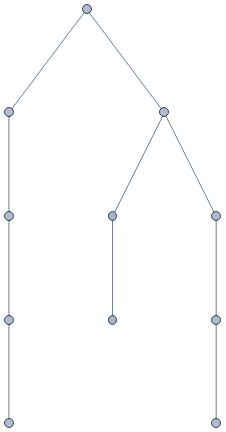
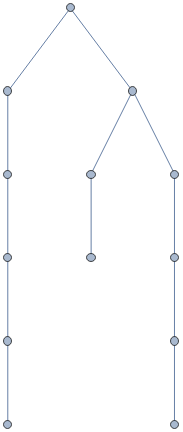
Flatten[Table[eq[Nest[s,0,i+j],plus[Nest[s,0,i],Nest[s,0,j]]],{i,3},{j,3}]]
Out[]=
{eq[s[s[0]],plus[s[0],s[0]]],eq[s[s[s[0]]],plus[s[0],s[s[0]]]],eq[s[s[s[s[0]]]],plus[s[0],s[s[s[0]]]]],eq[s[s[s[0]]],plus[s[s[0]],s[0]]],eq[s[s[s[s[0]]]],plus[s[s[0]],s[s[0]]]],eq[s[s[s[s[s[0]]]]],plus[s[s[0]],s[s[s[0]]]]],eq[s[s[s[s[0]]]],plus[s[s[s[0]]],s[0]]],eq[s[s[s[s[s[0]]]]],plus[s[s[s[0]]],s[s[0]]]],eq[s[s[s[s[s[s[0]]]]]],plus[s[s[s[0]]],s[s[s[0]]]]]}
In[]:=
ExpressionTree/@%
Out[]=

,
,
,
,
,
,
,
,

In[]:=
ExpressionGraph/@Flatten[Table[eq[Nest[s,0,i+j],plus[Nest[s,0,i],Nest[s,0,j]]],{i,3},{j,3}]]
Out[]=

,
,
,
,
,
,
,
,


Hyperedges are not enough to represent expressions; would have to use Polish notation

Metametalogic

Law of inference: takes expressions and returns expressions

Use a tree analog of the hypergraph

Instead of ordered lists as hyperedges, we use trees/expressions as hyperedges

Metalogic

- One theorem is applied to another by substitution
or - Modus ponens

E.g. in Lean, statements transforms proofs to proofs [or types to types]

plus: Integer , Integer  Integer

What is a mathematical observer like?

Physical observers: extended in space, extended in branchial space

Xerxes claim: mathematical observer is bringing consistency to different proof chains

Math observer finds a reference frame in which the things they see can be considered consistent

Inconsistency:
generates both a statement and its negation
or it gives a thing we don’t like

Foliation / reference is a slicing of the multiway graph of theorem derivations

Branchlike hypersurface would be the irredundant version of math

Speed of proof...

How are mathematical statements laid out in mathematical space?

​

Issue is consistency through time

Can a mathematician re-prove a theorem they proved before?
Is there a black hole that prevents re-proving a theorem?
Maybe you don’t reprove the same theorem with the same atoms, but somehow an equivalent theorem

[Linear types: you “use up” elements so they are not re-used]

Mathematical consciousness: consistency through time

Level of granularity for mathematical observer?

Abstraction is coarse graining...

Is computational boundedness for math observer a boundedness in the selection of statements?

One way to pick your “valid statements” is to do a proof from axioms [only reaches a certain distance in a certain time because of the proof cone]
Or you could pick by intuition [ with a computational bounded scheme ] : is what you’ve picked consistent? [i.e. can’t derive something you don’t like]

Possibility of parallel transport of one field of math to another [~duality]

Energy momentum would disrupt the parallel transport
Proof redundancy : positive curvature
To get proof redundancy: need higher-level math knowledge [??]

Isomorphisms between observers : inertial frames [?]

More complicated proofs : more complicated frame transformations

Is there a continuity equation for matter? Is there a source term for mathematical activity

Pure motion ~ parallel transport

Simplest case: recasting the math in some isomorphic form
Decidable theories obstruct transport in metamathematical space

For an observer with a given coord system, when does parallel transport fail?

Observer picks fiducial statements; which then follow Brownian motion

Time is generated by the collective activities of mathematicians

This is the creation of “discovered mathematics”

In the ruliad, sensing other fibers is like seeing more mass...
Or is more mass just being created?