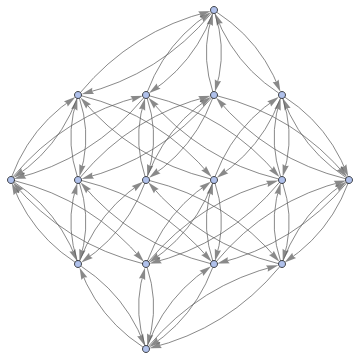
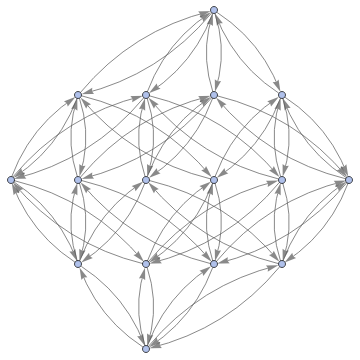
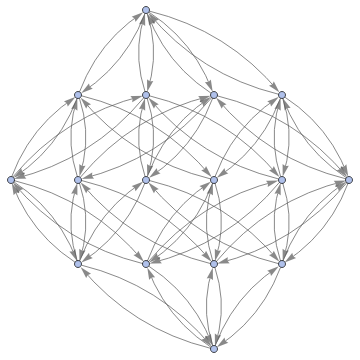
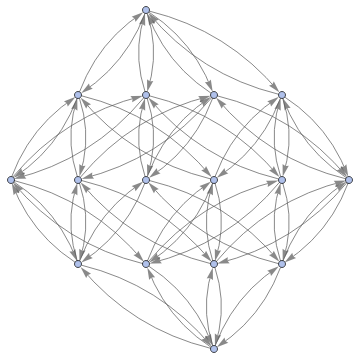
In[]:=
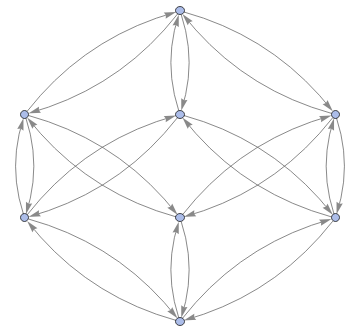
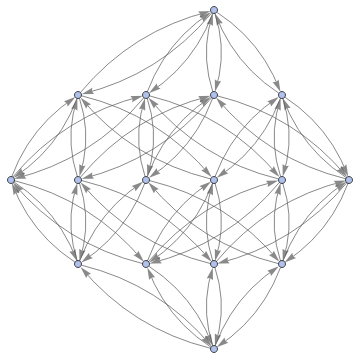
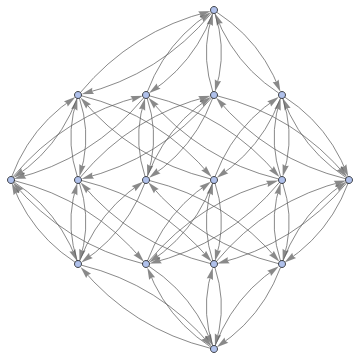
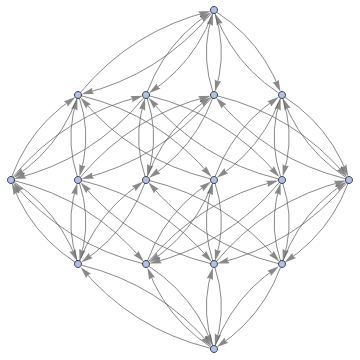
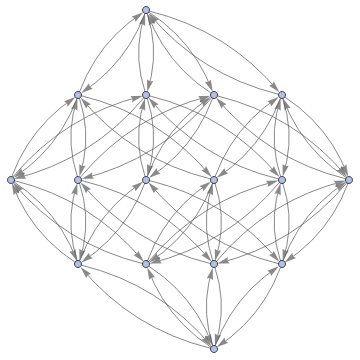
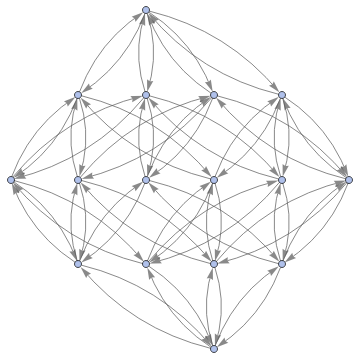
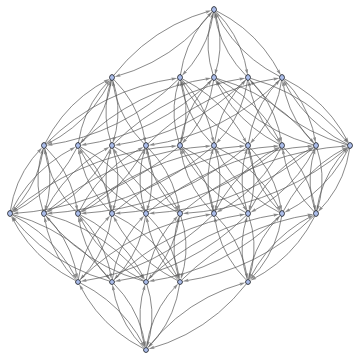
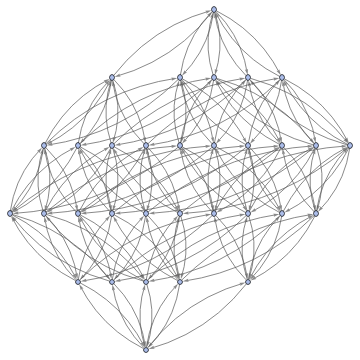
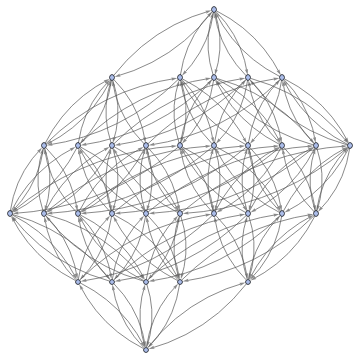
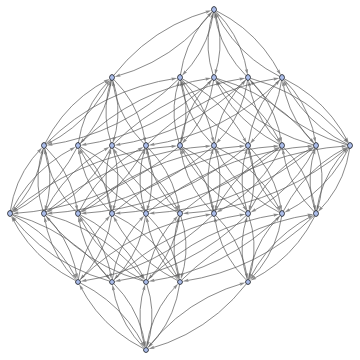
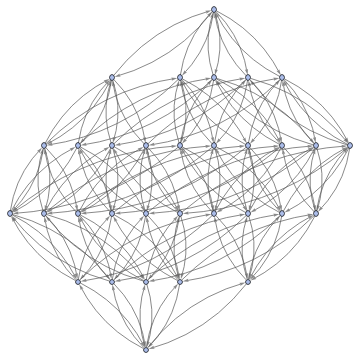
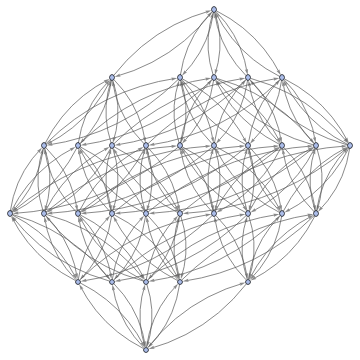
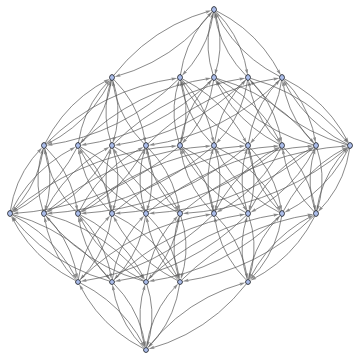
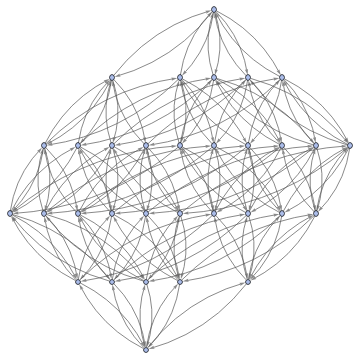
Graph3D[ResourceFunction["MultiwayFunctionSystem"][Values[substitutionLemmas[#,x_∘y_<->y_∘x_]]&,((a∘b)∘(c∘d))∘(e∘f),5,"StatesGraphStructure"],GraphLayout"LayeredDigraphEmbedding",AspectRatio1]
In[]:=
Groupings[Array[a,4],SmallCircle->2]
Out[]=
{((a[1]∘a[2])∘a[3])∘a[4],a[1]∘((a[2]∘a[3])∘a[4]),(a[1]∘(a[2]∘a[3]))∘a[4],a[1]∘(a[2]∘(a[3]∘a[4])),(a[1]∘a[2])∘(a[3]∘a[4])}
In[]:=
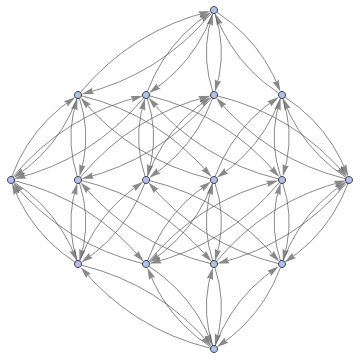
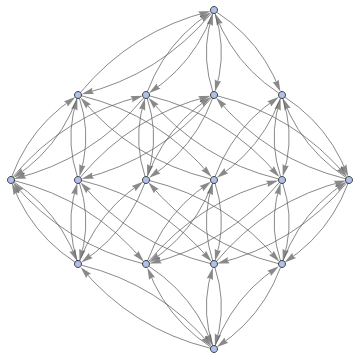
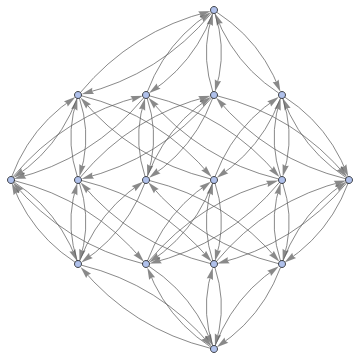
Graph[ResourceFunction["MultiwayFunctionSystem"][Values[substitutionLemmas[#,x_∘y_<->y_∘x_]]&,#,8,"StatesGraphStructure"],GraphLayout"LayeredDigraphEmbedding",AspectRatio1]&/@Groupings[Array[a,4],SmallCircle->2]
Out[]=
,
,
,
,
In[]:=
Graph[ResourceFunction["MultiwayFunctionSystem"][Values[substitutionLemmas[#,x_∘y_<->y_∘x_]]&,#,8,"StatesGraphStructure"],GraphLayout"LayeredDigraphEmbedding",AspectRatio1]&/@Groupings[Array[a,5],SmallCircle->2]
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
,
In[]:=
VertexCount/@%
Out[]=
{16,16,16,16,16,16,16,16,16,16,16,16,16,16}
In[]:=
Map[Graph[ResourceFunction["MultiwayFunctionSystem"][Values[substitutionLemmas[#,x_∘y_<->y_∘x_]]&,#,8,"StatesGraphStructure"],GraphLayout"LayeredDigraphEmbedding",AspectRatio1]&,RandomSample[Groupings[Array[a,6],SmallCircle->2],10]]
Out[]=
,
,
,
,
,
,
,
,
,
In[]:=
VertexCount/@%
Out[]=
{32,32,32,32,32,32,32,32,32,32}
In[]:=
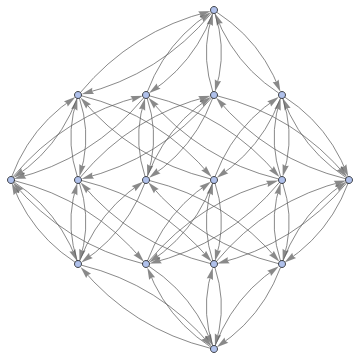
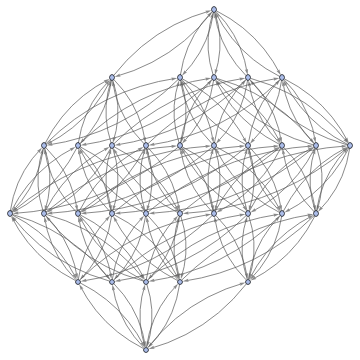
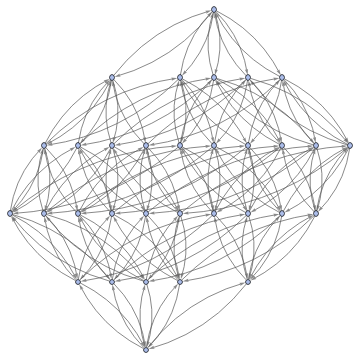
Graph3D[ResourceFunction["MultiwayFunctionSystem"][Values[substitutionLemmas[#,x_∘y_<->y_∘x_]]&,((a∘b)∘(c∘d))∘(e∘f),5,"StatesGraphStructure"],GraphLayout"LayeredDigraphEmbedding",AspectRatio1]
Out[]=
while when applied to (a∘b)∘(c∘d) we get:
All this is a bit more familiar in the case of groups---though the typical axioms for these are slightly more complicated:
All this is a bit more familiar in the case of groups---though the typical axioms for these are slightly more complicated:
We can think of our expressions as corresponding to words in the semigroup. So in this case what we’re seeing is that there are an infinite number of equivalences between words.
In the mathematical
In the mathematical
So what this means is that in this case there are an infinite number of equivalences
But what is the mathematical significance of this? Each expression corresponds to a “word” in a presentation of the semigroup. And our multiway graph then tells us a certain set of words that are equivalent according to the axioms and relations of the semigroup.
under the captures what collection of words In effect our multiway graph captures
under the captures what collection of words In effect our multiway graph captures
This is an Abelian semigroup.....
Because axioms don’t change size, result from starting from a given expression will be finite.....
Adding more “relations” more theorems will be true....
E.g. if just commutative have XXX == XXXX ; associative XXX == XXX
Because axioms don’t change size, result from starting from a given expression will be finite.....
Adding more “relations” more theorems will be true....
E.g. if just commutative have XXX == XXXX ; associative XXX == XXX
More theorems are true.....
[ Relation to Cayley graph for group ]
Generated Variables
Generated Variables
If we start with a∘a and do no unification, we’ll get:
With uniquification, but not canonicalization we’ll get a pure tree:
But with canonicalization this is reduced to:
A confusing feature of this particular example is that this same result would have been obtained just by canonicalizing the original “assume-all-x_’s-are-the-same” case.
Rules Applied to Rules
Rules Applied to Rules
Rules where we keep applying a rule to each side
Rules where we keep applying a rule to each side
The dot just drops its first element (like the K combinator)
What does a proof look like here?
Forward light cone of the initial expr intersected with the past light cone of the destination.......
Finding proofs
Finding proofs
Alternative Simple Case
Alternative Simple Case