In[]:=
Subsets[Range[4]]
Out[]=
{{},{1},{2},{3},{4},{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},{1,2,3},{1,2,4},{1,3,4},{2,3,4},{1,2,3,4}}
In[]:=
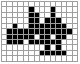
Function[rr,SeedRandom[2342];Labeled[ArrayPlot[#/.{(2|3|4)->0},Mesh->True,ImageSize->80]&@Last[AggregationArrayData[rr][{Last[RandomTotalisticAggregation[{rr,Join[IdentityMatrix[2],-IdentityMatrix[2]]},Position[CrossMatrix[{1,1}],1]-2,50]]}]],rr]]/@Subsets[Range[4]]
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
{} |
{1} |
{2} |
{3} |
{4} |
{1,2} |
{1,3} |
{1,4} |
{2,3} |
{2,4} |
{3,4} |
{1,2,3} |
{1,2,4} |
{1,3,4} |
{2,3,4} |
{1,2,3,4} |
In[]:=
Function[rr,SeedRandom[2342];Labeled[ArrayPlot[#/.{(2|3|4)->0},ImageSize->80]&@Last[AggregationArrayData[rr][{Last[RandomTotalisticAggregation[{rr,Join[IdentityMatrix[2],-IdentityMatrix[2]]},Position[CrossMatrix[{1,1}],1]-2,1000]]}]],rr]]/@Subsets[Range[4]]
Out[]=
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
{} |
{1} |
{2} |
{3} |
{4} |
{1,2} |
{1,3} |
{1,4} |
{2,3} |
{2,4} |
{3,4} |
{1,2,3} |
{1,2,4} |
{1,3,4} |
{2,3,4} |
{1,2,3,4} |
ArrayPlot[DataRange]
In[]:=
AbsoluteOptions
,PlotRange
Out[]=
{PlotRange{{0.,51.},{0.,45.}}}
In[]:=
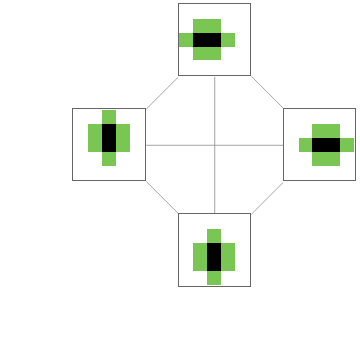
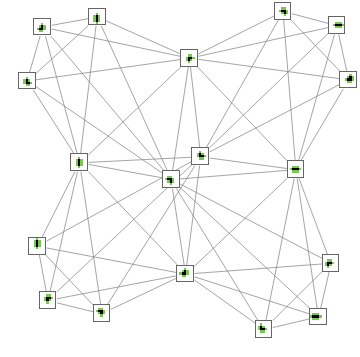
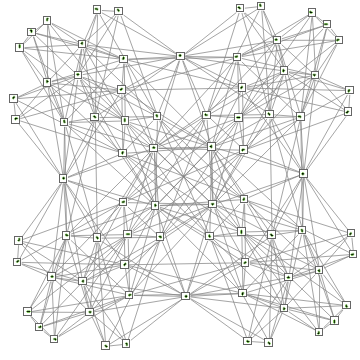
AddVertexArrayPlots[Range[4]]/@ResourceFunction["BranchialGraphs"][Graph[AddVertexArrayPlots[Range[4]][TotalisticAggregationMultiwayGraph[{Range[4],Join[IdentityMatrix[2],-IdentityMatrix[2]]},{{0,0}},3]],AspectRatio->1/4,VertexSize->1.5]]
Out[]=
1
,2
,3
,4
In[]:=
Graph3D[EdgeList[#]]&/@%
Out[]=
1 ,3
,3 ,4
,4
,2
In[]:=
Graph3D/@ResourceFunction["BranchialGraphs"][Graph[AddVertexArrayPlots[Range[4]][TotalisticAggregationMultiwayGraph[{Range[4],Join[IdentityMatrix[2],-IdentityMatrix[2]]},{{0,0}},4]],AspectRatio->1/4,VertexSize->1.5]]
Out[]=
1 ,2
,2 ,3
,3 ,4
,4 ,5
,5
8-cell case
8-cell case
3D
3D
6-neighbor case
6-neighbor case