Out[]=
In[]:=
TotalisticAggregationMultiwayGraph[{Range[4],Join[IdentityMatrix[2],-IdentityMatrix[2]]},{{0,0}},2]
Out[]=
In[]:=
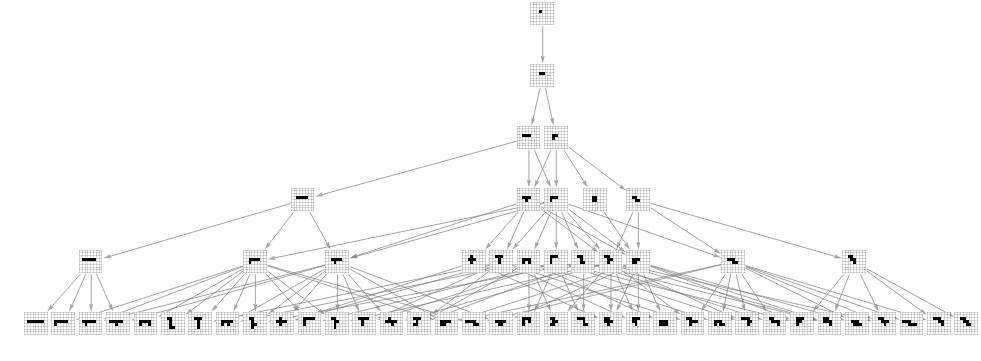
Graph[AddVertexArrayPlots[Range[4]][TotalisticAggregationMultiwayGraph[{Range[4],Join[IdentityMatrix[2],-IdentityMatrix[2]]},{{0,0}},5,"Canonicalize"->True]],AspectRatio->1/3,VertexSize->1.8,GraphLayout->"LayeredDigraphEmbedding"]
Out[]=
In[]:=
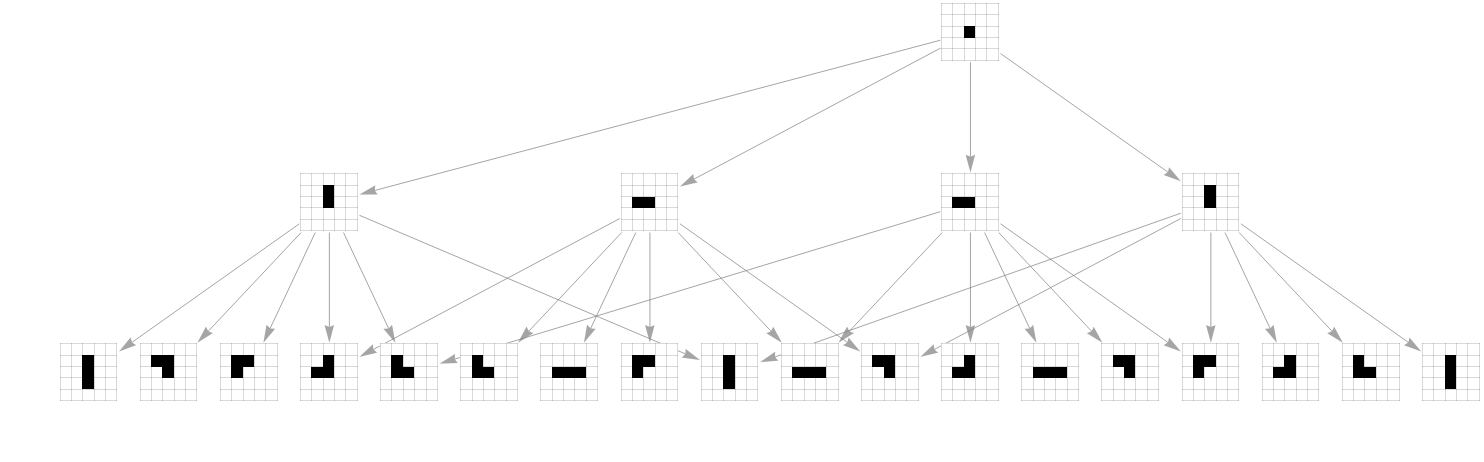
Graph[AddVertexArrayPlots[Range[4]][TotalisticAggregationMultiwayGraph[{Range[4],Join[IdentityMatrix[2],-IdentityMatrix[2]]},{{0,0}},2]],AspectRatio->1/4,VertexSize->1.5]
In[]:=
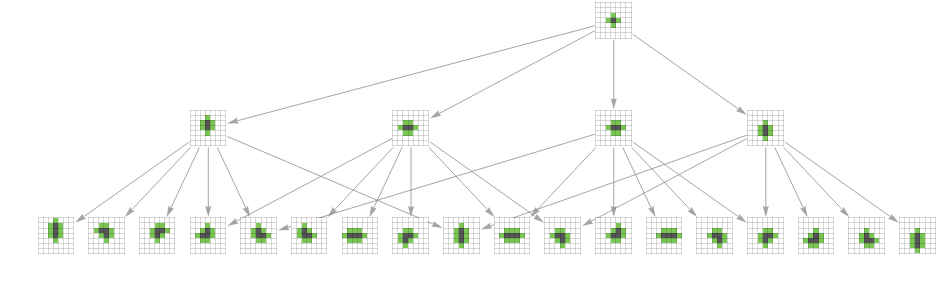
Graph[AddVertexArrayPlots[Range[4]][TotalisticAggregationMultiwayGraph[{Range[4],Join[IdentityMatrix[2],-IdentityMatrix[2]]},{{0,0}},2],ColorRules->$GrowthColors],AspectRatio->1/4,VertexSize->1.5]
Out[]=
In[]:=
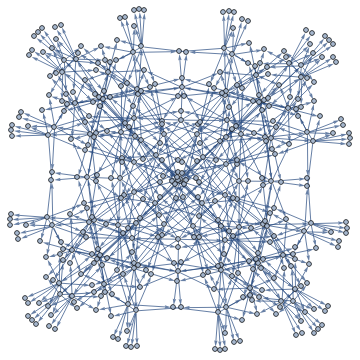
TotalisticAggregationMultiwayGraph[{Range[4],Join[IdentityMatrix[2],-IdentityMatrix[2]]},{{0,0}},4]
Out[]=
In[]:=
Length/@ResourceFunction["VertexStratify"][%]
Out[]=
{1,4,18,76,315}
In[]:=
With[{g1=TotalisticAggregationMultiwayGraph[{Range[4],Join[IdentityMatrix[2],-IdentityMatrix[2]]},{{0,0}},2]},KeyValueMap[Labeled[AggregationArrayPlot[Range[4]][#1],#2]&,Counts[CanonicalizeGrowthData/@VertexList[g1]]]]
Out[]=
,
,
,
1 |
4 |
6 |
12 |
Constrained Case
Constrained Case
{3}
{3}
initial conditions:
initial conditions:
8 Neighbors
8 Neighbors
SAT solving
SAT solving
{3} case
{3} case
{2} case
{2} case
Monte Carlo
Monte Carlo
More
More
Finding holes
Finding holes